Surface Area & Volume of Cube & Cuboid | Mathematics for EmSAT Achieve PDF Download
Surface Area of Cuboid
A cuboid is a three-dimensional figure bounded by six rectangular planes, having a different magnitude of length, width and height. If you look around and you can see a box, brick or anything in the shape of a rectangle, it could be cuboid. A cuboid (3-dimensional) can be seen made up of rectangles (2-dimensional) of different dimensions when seen from any of the ends. In this article, we are going to discuss the definition of cuboid, total and lateral surface area of a cuboid in a detailed way.
Cuboid Definition
A cuboid is a three-dimensional figure or solid which has six rectangular sides called faces. Each face of a cuboid is a rectangle and all of its corners are 90-degrees. It has 8 vertices and 12 edges. The opposite faces of a cuboid are always equal. It means that the opposite surfaces of the cuboid are in the same dimension. The measures of the cuboid are the Total Surface Area (TSA), Lateral or curved Surface Area (CSA) and volume. The surface areas are measured in terms of square units, whereas the volume of the cube is measured in terms of cubic units.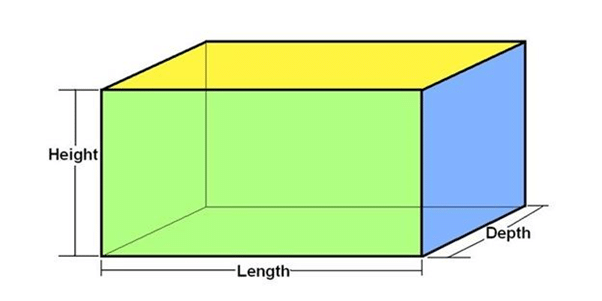
Area of Cuboid
The area of a cuboid refers to the surface area as the cuboid is a three dimensional solid. Thus, the area of cuboid can be calculated using the formula of area of rectangle, since the faces of a cuboid are in a rectangular shape.
Cuboid Surface Area
The surface area of the cuboid can be of two types:
- Total Surface Area
- Lateral Surface Area or Curved Surface Area
Surface Area of Cuboid Formula
Before going into the concept of area, let us denote the dimensions of a cuboid, which are, Length, Width, and Height are represented by l, w, h, respectively.
1. Total Surface Area of a Cuboid
The Total surface area of a cuboid (TSA) is equal to the sum of the areas of it’s 6 rectangular faces, which is given by:
Total Surface Area of a Cuboid (TSA) = 2 (lw + wh + lh) square units
The above formula gives the total surface area of a cuboid having all six faces.
2. Lateral Surface Area of a Cuboid
The lateral surface area of a cuboid is the sum of 4 planes of a rectangle, leaving the top (upper) and the base (lower) surface. Mathematically, the Lateral Surface Area of a cuboid (LSA) is given as:
Lateral Surface Area of a cuboid (LSA) = 2 (lh + wh) = 2 h (l + w) square units
Total Surface Area of a Cuboid Derivation
As the cuboid has six rectangular faces, the total surface area of the cuboid is calculated as follows:
Assume that, l, w, h be the length, width, and height of the cuboid respectively.
Thus,
The front face area of cuboid = l x h
The back face area of the cuboid = l x h
The top face area of the cuboid = l x w
The bottom face area of the cuboid = l x w
The left face area of the cuboid = h x w
The right face area of cuboid = h x w
Hence, the total surface area is the sum of all the faces of a cuboid, then the TSA of a cuboid is:
Total Surface Area of Cuboid = lh + lh + lw + lw + hw + hw
Total Surface Area of Cuboid = 2 lh + 2 lw + 2 hw
Total Surface Area of Cuboid = 2 (lh + lw + hw)
Therefore, the total surface area of the cuboid is 2 (lh + lw + hw) square units.
Surface Area of Cuboid Examples
Example 1: Given below is a cuboid having its dimension given as length = 8 cm, width = 6 cm and height = 5 cm, find the TSA of a cuboid.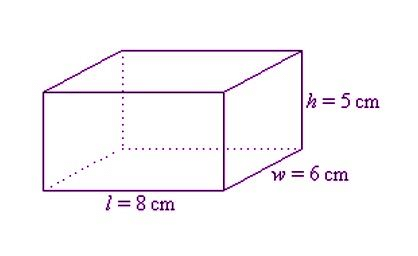 Solution: Given:
Solution: Given:
h = 5 cm
w = 6 cm
l = 8 cm
Using the formula: TSA = 2 (lw + wh + hl)
2((8 × 6) + (6 × 5) + (5 × 8))
= 2(48 + 30 + 40)
= 2(118)
= 236
So, the total surface area of this cuboid is 236 cm2.
Example 2: The dimensions of a cuboid are given as follows:
Length = 4.8 cm
Width = 3.4 cm
Height = 7.2 cm.
Find the Total Surface area and the Lateral Surface area.
Solution: The total surface area is given as
TSA = 2 (lw + wh + hl)
=2((4.8 × 3.4) + (3.4 × 7.2) + (7.2 × 4.8))
= 2(16.32 + 24.48 + 34.56) = 2(75.36) cm2
Therefore, TSA of a cuboid = 150.72 cm
Also, the lateral surface area = 2 h (l + w)
= 2 × 7.2 (4.8 + 3.4)
= 14.4 (8.2) = 118.08
Therefore, LSA of a cuboid = 118.08 cm2.
Surface Area Of Cube
Surface area of cube is the sum of areas of all the faces of cube, that covers it. The formula for surface area is equal to six times of square of length of the sides of cube. It is represented by 6a2, where a is the side length of cube.It is basically the total surface area. Also, learn Volume Of A Cube.
When a cube is kept in a three-dimensional space, the area occupied by the sides of the cube in the space is called surface area of cube. In real world, we have been surrounded by many solid objects which have their own area as well volume. The area defines the region occupied by the objects and volume defines the space contained inside that object. The basic solid shapes or 3D shapes which we have learned till now in geometry are:
- Cube
- Cuboid
- Cylinder
- Cone
- Sphere
Surface Area of Cube Definition
The definition of surface area of a given cube states that if the total surface area is equal to the sum of all the areas of the faces of the cube. Since the cube has six faces, therefore, the total surface area of the cube will be equal to sum of all six faces of cube.
Since, the surface of the cube is in square shape. Hence, area of each face of the cube is equal to square of edge. Let the length of edge of cube is a.
Therefore, area of one face = a2 [By area of square formula]
There are total 6 faces. Therefore,
TSA of cube = a2 + a2 + a2 + a2 + a2 +a2
TSA of cube = 6a2
A cube consists of ‘n’ number of square units. Hence the space covered by these square units on the surface of the cube is the surface area. Basically, the surface area is the sum of all the area of all the shapes that cover the surface of the shape or object. In the case of a cube, there are 6 faces. So the surface area will be sum of all the area of six faces.
Let us derive the formula for surface area for a given cube, to solve problems based on it.
Surface Area of a Cube Formula
As per the definition of the cube, we know, the cube consists of 6 square faces. Let us consider, a cube whose length of the edges is ‘a’.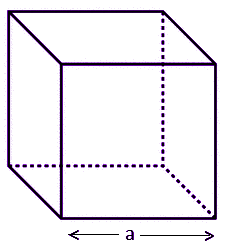 Now, we know, by the formula of area of a square;
Now, we know, by the formula of area of a square;
Area = Side2 = a2
Therefore, the total surface area of a cube = 6 × (area of each side)
= 6 × a2 = 6a2 Square Unit
TSA = 6 a2
Length of Edge of the Cube
From the formula of the surface area of the cube, we can also find the length of the edge of the cube by rearranging the formula, such as;
A = 6 (side)2
side2 = A / 6
side = √(A / 6) = Edge length
where A is the area.
Surface Area of Cube Examples
Example 1: Calculate the cost required to paint an aquarium which is in cube shape having an edge length of 10m. If the painting cost of an aquarium is INR 3/m2.
Solution: Total surface area of aquarium = 6 (side)2
= 6 (10)2
= 600 sq.m
Total cost of painting the aquarium = 3 × 600 = Rs.1800
Example 2: If the sidewall of a cubic structure have length 7m, then find the total surface area.
Solution: Given, the length of the sidewall = 7m
As per the formula, we know;
TSA = 6a2
TSA = 6 x 7 x 7 = 294 sq.m
Example 3: Find the length of the edge of the cube, if its area is 2400 sq.cm.
Solution: Given, area = 2400 sq.cm.
We know,
Length of edge of cube = √(A / 6) = √(2400 / 6) = √400 = 20 cm.
Volume Of Cuboid
Volume of cuboid is the total space occupied by the cuboid in a three-dimensional space. A cuboid is a three-dimensional structure having six rectangular faces. These six faces of the cuboid exist as a pair of three parallel faces. Therefore, the volume is a measure based on the dimensions of these faces, i.e. length, width and height. Surface area of cuboid is the total area covered by its faces.
Volume of Cuboid = Length x Width x Height (Cubic Unit)
When the area of the faces of a cuboid is same, we call this cuboid as a cube. The area of all the faces of a cube is the same as they are all squares. Read about 3d shapes here.
Think of a scenario where we need to calculate the amount of sugar that can be accommodated in a cuboidal box. In other words, we mean to calculate the capacity of this box. The capacity of a cuboidal box is basically equal to the volume of cuboid involved.
In this, let us discuss what is a volume of a cuboid, its formula, along with the volume of a cuboid prism and a cube example.
What is the Volume of a Cuboid?
The volume of a three-dimensional shape Cuboid, in general, is equal to the amount of space occupied by the shape cuboid. The term “Solid Rectangle” is also known as a cuboid, because all the faces of a cuboid are rectangular. In rectangular cuboid, all the angles are at right angles and the opposite faces of a cuboid are equal.
The general formula for the calculation of the volume of a cuboid is given below.
The volume of cuboid: The volume of a cuboid is given by the product of its dimensions.
The volume of a cuboid of length ‘l’, breadth ‘b’, height ‘h’ = l × b × h cubic units.
Total Surface Area of Cuboid
The total surface area of a cuboid is equal to the sum of the areas of the six rectangular faces whereas the Lateral surface area of a cuboid equal to the sum of the four rectangular faces, in which two rectangular faces of the top and bottom faces are excluded. The formula for the total surface area and lateral surface area of a cuboid is given as:
Total Surface Area of a Cuboid = 2 (lb + hb + lh) square units
Lateral Surface Area of a Cuboid = 2h (l + b)
Volume of a Cuboid Prism
A cuboid prism or a rectangular prism is the same as the cuboid. It has 6 faces, 8 vertices, and 12 edges. When a cuboid prism or a rectangular prism has a rectangular cross-section. A prism is called right prism when the angle between the base and the sides are at right angles. Also, the top and the bottom surfaces are in the same shape and size. The volume of the cuboid prism is given as:
Volume of a cuboid prism or rectangular prism, V = length × breadth × height (cubic units).
Volume of a Cube
Cuboid in which length of each edge is equal is known as a cube. Thus, Volume of a cube of side ‘a’ = a3.
Solved Examples
Example 1: Calculate the length of the edge of a cube-shaped container of volume 216 m3.
Solution: Volume of a cube = a3
=> a3 = 216
=> a = 6 m
Example 2: Calculate the amount of air that can be accumulated in a room that has a length of 5 m, breadth of 6 m and a height of 10 m.
Solution: Amount of air that can be accumulated in a room = capacity of the room = volume of a cuboid
Volume of cuboid = l × b × h = 5 × 6 × 10 = 300 m3
Thus, this room can accommodate the maximum of 300 m3 of air.
Practice Questions
Q. Find the volume of cuboid with following dimensions:
- Length = 15 cm, Breadth = 50 cm and Height = 22 cm
- Length = 7 m, Breadth = 3 m and Height = 5 m
- Length = 2 m, Breadth = 2.5 m and Height = 1.5 m
- Length = 80 cm, Breadth = 20 cm and Height = 44 cm
- Length = 1.7 m, Breadth = 1.5 m and Height = 1 m
|
141 videos|213 docs|254 tests
|
FAQs on Surface Area & Volume of Cube & Cuboid - Mathematics for EmSAT Achieve
| 1. How do you calculate the surface area of a cube? |  |
| 2. What is the formula for finding the volume of a cuboid? |  |
| 3. Can you calculate the volume of a cube using its surface area? |  |
| 4. How can you find the length of a side if the surface area of a cube is given? |  |
| 5. Is the surface area of a cube always greater than its volume? |  |

|
Explore Courses for EmSAT Achieve exam
|

|

















