Dijkstra’s Shortest Path Algorithm | Algorithms - Computer Science Engineering (CSE) PDF Download
Greedy Algo-7
Given a graph and a source vertex in the graph, find shortest paths from source to all vertices in the given graph.
Dijkstra’s algorithm is very similar to Prim’s algorithm for minimum spanning tree. Like Prim’s MST, we generate a SPT (shortest path tree) with given source as root. We maintain two sets, one set contains vertices included in shortest path tree, other set includes vertices not yet included in shortest path tree. At every step of the algorithm, we find a vertex which is in the other set (set of not yet included) and has a minimum distance from the source.
Below are the detailed steps used in Dijkstra’s algorithm to find the shortest path from a single source vertex to all other vertices in the given graph.
Algorithm
- Create a set sptSet (shortest path tree set) that keeps track of vertices included in shortest path tree, i.e., whose minimum distance from source is calculated and finalized. Initially, this set is empty.
- Assign a distance value to all vertices in the input graph. Initialize all distance values as INFINITE. Assign distance value as 0 for the source vertex so that it is picked first.
- While sptSet doesn’t include all vertices
(a) Pick a vertex u which is not there in sptSet and has minimum distance value.
(b) Include u to sptSet.
(c) Update distance value of all adjacent vertices of u. To update the distance values, iterate through all adjacent vertices. For every adjacent vertex v, if sum of distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v.
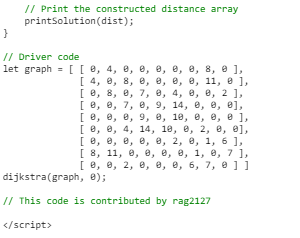
Let us understand with the following example: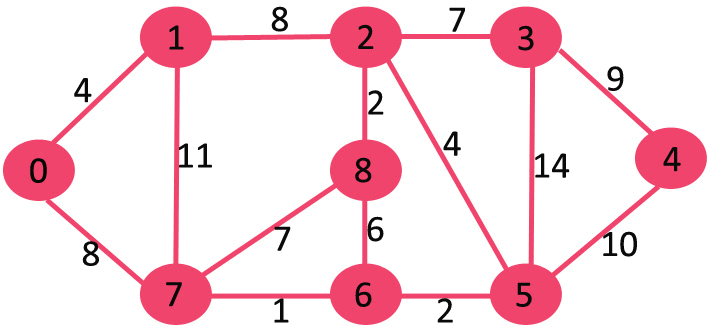 The set sptSet is initially empty and distances assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with minimum distance value. The vertex 0 is picked, include it in sptSet. So sptSet becomes {0}. After including 0 to sptSet, update distance values of its adjacent vertices. Adjacent vertices of 0 are 1 and 7. The distance values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their distance values, only the vertices with finite distance values are shown. The vertices included in SPT are shown in green colour.
The set sptSet is initially empty and distances assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with minimum distance value. The vertex 0 is picked, include it in sptSet. So sptSet becomes {0}. After including 0 to sptSet, update distance values of its adjacent vertices. Adjacent vertices of 0 are 1 and 7. The distance values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their distance values, only the vertices with finite distance values are shown. The vertices included in SPT are shown in green colour.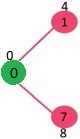
Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). The vertex 1 is picked and added to sptSet. So sptSet now becomes {0, 1}. Update the distance values of adjacent vertices of 1. The distance value of vertex 2 becomes 12.
Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). Vertex 7 is picked. So sptSet now becomes {0, 1, 7}. Update the distance values of adjacent vertices of 7. The distance value of vertex 6 and 8 becomes finite (15 and 9 respectively).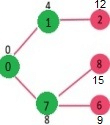
Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). Vertex 6 is picked. So sptSet now becomes {0, 1, 7, 6}. Update the distance values of adjacent vertices of 6. The distance value of vertex 5 and 8 are updated.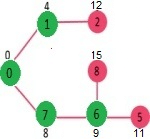
We repeat the above steps until sptSet does include all vertices of given graph. Finally, we get the following Shortest Path Tree (SPT).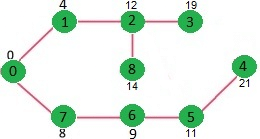
How to implement the above algorithm?
We use a boolean array sptSet[] to represent the set of vertices included in SPT. If a value sptSet[v] is true, then vertex v is included in SPT, otherwise not. Array dist[] is used to store shortest distance values of all vertices.
- C++


- Java


- Python


- C#



- Javascript



Output:
Notes:
- The code calculates shortest distance, but doesn’t calculate the path information. We can create a parent array, update the parent array when distance is updated (like prim’s implementation) and use it show the shortest path from source to different vertices.
- The code is for undirected graph, same dijkstra function can be used for directed graphs also.
- The code finds shortest distances from source to all vertices. If we are interested only in shortest distance from the source to a single target, we can break the for the loop when the picked minimum distance vertex is equal to target (Step 3.a of the algorithm).
- Time Complexity of the implementation is O(V2). If the input graph is represented using adjacency list, it can be reduced to O(E log V) with the help of binary heap. Please see Dijkstra’s Algorithm for Adjacency List Representation for more details.
- Dijkstra’s algorithm doesn’t work for graphs with negative weight cycles, it may give correct results for a graph with negative edges. For graphs with negative weight edges and cycles, Bellman–Ford algorithm can be used, we will soon be discussing it as a separate post.
Greedy Algo-8
We have discussed Dijkstra’s algorithm and its implementation for adjacency matrix representation of graphs. The time complexity for the matrix representation is O(V^2). In this post, O(ELogV) algorithm for adjacency list representation is discussed.
Dijkstra’s algorithm, two sets are maintained, one set contains list of vertices already included in SPT (Shortest Path Tree), other set contains vertices not yet included. With adjacency list representation, all vertices of a graph can be traversed in O(V+E) time using BFS. The idea is to traverse all vertices of graph using BFS and use a Min Heap to store the vertices not yet included in SPT (or the vertices for which shortest distance is not finalized yet). Min Heap is used as a priority queue to get the minimum distance vertex from set of not yet included vertices. Time complexity of operations like extract-min and decrease-key value is O(LogV) for Min Heap.
Following are the detailed steps:
- Create a Min Heap of size V where V is the number of vertices in the given graph. Every node of min heap contains vertex number and distance value of the vertex.
- Initialize Min Heap with source vertex as root (the distance value assigned to source vertex is 0). The distance value assigned to all other vertices is INF (infinite).
- While Min Heap is not empty, do following
(a) Extract the vertex with minimum distance value node from Min Heap. Let the extracted vertex be u.
(b) For every adjacent vertex v of u, check if v is in Min Heap. If v is in Min Heap and distance value is more than weight of u-v plus distance value of u, then update the distance value of v.
Let us understand with the following example. Let the given source vertex be 0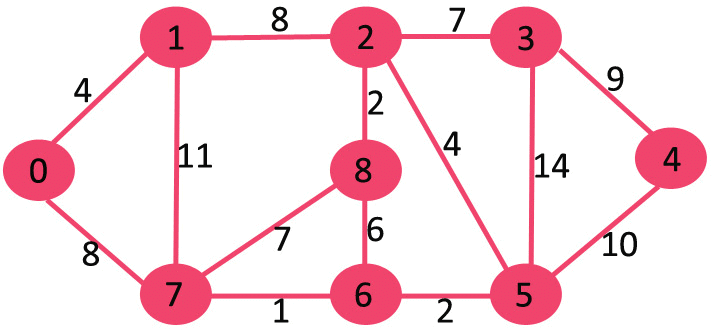
Initially, distance value of source vertex is 0 and INF (infinite) for all other vertices. So source vertex is extracted from Min Heap and distance values of vertices adjacent to 0 (1 and 7) are updated. Min Heap contains all vertices except vertex 0.
The vertices in green color are the vertices for which minimum distances are finalized and are not in Min Heap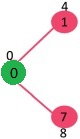
Since distance value of vertex 1 is minimum among all nodes in Min Heap, it is extracted from Min Heap and distance values of vertices adjacent to 1 are updated (distance is updated if the a vertex is in Min Heap and distance through 1 is shorter than the previous distance). Min Heap contains all vertices except vertex 0 and 1.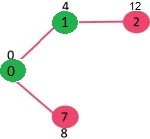
Pick the vertex with minimum distance value from min heap. Vertex 7 is picked. So min heap now contains all vertices except 0, 1 and 7. Update the distance values of adjacent vertices of 7. The distance value of vertex 6 and 8 becomes finite (15 and 9 respectively).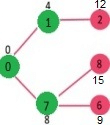
Pick the vertex with minimum distance from min heap. Vertex 6 is picked. So min heap now contains all vertices except 0, 1, 7 and 6. Update the distance values of adjacent vertices of 6. The distance value of vertex 5 and 8 are updated.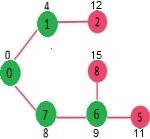
Above steps are repeated till min heap doesn’t become empty. Finally, we get the following shortest path tree.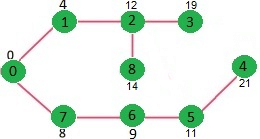
- C++









- Python






Output: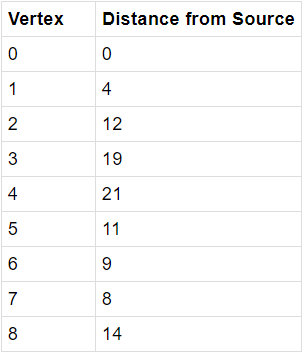
Time Complexity: The time complexity of the above code/algorithm looks O(V^2) as there are two nested while loops. If we take a closer look, we can observe that the statements in inner loop are executed O(V+E) times (similar to BFS). The inner loop has decreaseKey() operation which takes O(LogV) time. So overall time complexity is O(E+V)*O(LogV) which is O((E+V)*LogV) = O(ELogV)
Note that the above code uses Binary Heap for Priority Queue implementation. Time complexity can be reduced to O(E + VLogV) using Fibonacci Heap. The reason is, Fibonacci Heap takes O(1) time for decrease-key operation while Binary Heap takes O(Logn) time.
Notes:
- The code calculates shortest distance, but doesn’t calculate the path information. We can create a parent array, update the parent array when distance is updated (like prim’s implementation) and use it show the shortest path from source to different vertices.
- The code is for undirected graph, same dijekstra function can be used for directed graphs also.
- The code finds shortest distances from source to all vertices. If we are interested only in shortest distance from source to a single target, we can break the for loop when the picked minimum distance vertex is equal to target (Step 3.a of algorithm).
- Dijkstra’s algorithm doesn’t work for graphs with negative weight edges. For graphs with negative weight edges, Bellman–Ford algorithm can be used, we will soon be discussing it as a separate post.
(i) Printing Paths in Dijkstra’s Shortest Path Algorithm
(ii) Dijkstra’s shortest path algorithm using set in STL
|
81 videos|80 docs|33 tests
|
FAQs on Dijkstra’s Shortest Path Algorithm - Algorithms - Computer Science Engineering (CSE)
| 1. What is Dijkstra's shortest path algorithm? |  |
| 2. How does Dijkstra's algorithm work? |  |
| 3. What is the time complexity of Dijkstra's algorithm? |  |
| 4. Can Dijkstra's algorithm handle negative edge weights? |  |
| 5. What are some applications of Dijkstra's algorithm? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|