Huffman Coding | Algorithms - Computer Science Engineering (CSE) PDF Download

Greedy Algo-3

Huffman coding is a lossless data compression algorithm. The idea is to assign variable-length codes to input characters, lengths of the assigned codes are based on the frequencies of corresponding characters. The most frequent character gets the smallest code and the least frequent character gets the largest code.
The variable-length codes assigned to input characters are Prefix Codes, means the codes (bit sequences) are assigned in such a way that the code assigned to one character is not the prefix of code assigned to any other character. This is how Huffman Coding makes sure that there is no ambiguity when decoding the generated bitstream.
Let us understand prefix codes with a counter example. Let there be four characters a, b, c and d, and their corresponding variable length codes be 00, 01, 0 and 1. This coding leads to ambiguity because code assigned to c is the prefix of codes assigned to a and b. If the compressed bit stream is 0001, the de-compressed output may be “cccd” or “ccb” or “acd” or “ab”.
See this for applications of Huffman Coding.
There are mainly two major parts in Huffman Coding

• Build a Huffman Tree from input characters.
• Traverse the Huffman Tree and assign codes to characters.

1. Steps to build Huffman Tree
Input is an array of unique characters along with their frequency of occurrences and output is Huffman Tree. 

• Create a leaf node for each unique character and build a min heap of all leaf nodes (Min Heap is used as a priority queue. The value of frequency field is used to compare two nodes in min heap. Initially, the least frequent character is at root)
• Extract two nodes with the minimum frequency from the min heap.
• Create a new internal node with a frequency equal to the sum of the two nodes frequencies. Make the first extracted node as its left child and the other extracted node as its right child. Add this node to the min heap.
• Repeat steps#2 and #3 until the heap contains only one node. The remaining node is the root node and the tree is complete.

Let us understand the algorithm with an example:

Step 1: Build a min heap that contains 6 nodes where each node represents root of a tree with single node.
Step 2: Extract two minimum frequency nodes from min heap. Add a new internal node with frequency 5 + 9 = 14.

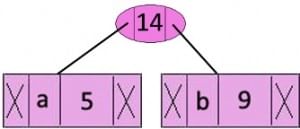
Now min heap contains 5 nodes where 4 nodes are roots of trees with single element each, and one heap node is root of tree with 3 elements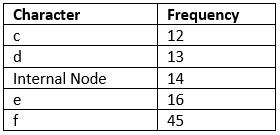

Step 3: Extract two minimum frequency nodes from heap. Add a new internal node with frequency 12 + 13 = 25

Now min heap contains 4 nodes where 2 nodes are roots of trees with single element each, and two heap nodes are root of tree with more than one nodes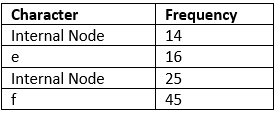

Step 4: Extract two minimum frequency nodes. Add a new internal node with frequency 14 + 16 = 30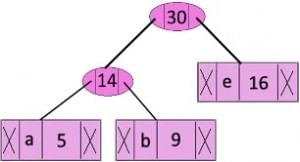

Now min heap contains 3 nodes.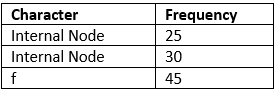

Step 5: Extract two minimum frequency nodes. Add a new internal node with frequency 25 + 30 = 55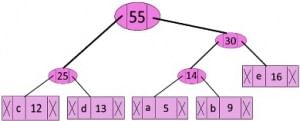

Now min heap contains 2 nodes.

Step 6: Extract two minimum frequency nodes. Add a new internal node with frequency 45 + 55 = 100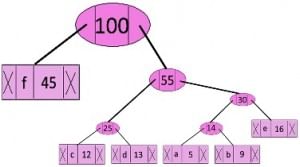

Now min heap contains only one node.

Since the heap contains only one node, the algorithm stops here.

2. Steps to print codes from Huffman Tree
Traverse the tree formed starting from the root. Maintain an auxiliary array. While moving to the left child, write 0 to the array. While moving to the right child, write 1 to the array. Print the array when a leaf node is encountered.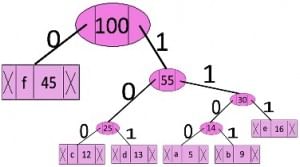

The codes are as follows: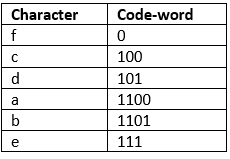

Below is the implementation of above approach:

(i) C

(ii) C++

(iii) C++

(iv) Java

(v) Python3




Output:
f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
Time complexity: O(nlogn) where n is the number of unique characters. If there are n nodes, extractMin() is called 2*(n – 1) times. extractMin() takes O(logn) time as it calles minHeapify(). So, overall complexity is O(nlogn).
If the input array is sorted, there exists a linear time algorithm. We will soon be discussing in our next post.

Applications of Huffman Coding

1. They are used for transmitting fax and text.
2. They are used by conventional compression formats like PKZIP, GZIP, etc.

 It is useful in cases where there is a series of frequently occurring characters.

Greedy Algo-4

Following is a O(n) algorithm for sorted input:
1. Create two empty queues.
2. Create a leaf node for each unique character and Enqueue it to the first queue in non-decreasing order of frequency. Initially second queue is empty.
3. Dequeue two nodes with the minimum frequency by examining the front of both queues. Repeat following steps two times

• If second queue is empty, dequeue from first queue.
• If first queue is empty, dequeue from second queue.
• Else, compare the front of two queues and dequeue the minimum.

4. Create a new internal node with frequency equal to the sum of the two nodes frequencies. Make the first Dequeued node as its left child and the second Dequeued node as right child. Enqueue this node to second queue.
5. Repeat steps#3 and #4 while there is more than one node in the queues. The remaining node is the root node and the tree is complete.

(i) C++

(ii) C










Output:
f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
Time complexity: O(n)
If the input is not sorted, it need to be sorted first before it can be processed by the above algorithm. Sorting can be done using heap-sort or merge-sort both of which run in Theta(nlogn). So, the overall time complexity becomes O(nlogn) for unsorted input.