Strongly Connected Components | Algorithms - Computer Science Engineering (CSE) PDF Download

Introduction

A directed graph is strongly connected if there is a path between all pairs of vertices. A strongly connected component (SCC) of a directed graph is a maximal strongly connected subgraph. For example, there are 3 SCCs in the following graph.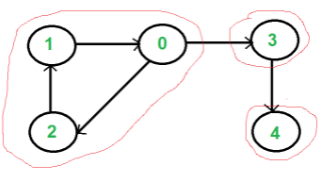

We can find all strongly connected components in O(V+E) time using Kosaraju’s algorithm.

Kosaraju’s Algorithm 

Following is detailed Kosaraju’s algorithm:

1. Create an empty stack ‘S’ and do DFS traversal of a graph. In DFS traversal, after calling recursive DFS for adjacent vertices of a vertex, push the vertex to stack. In the above graph, if we start DFS from vertex 0, we get vertices in stack as 1, 2, 4, 3, 0.
2. Reverse directions of all arcs to obtain the transpose graph.
3. One by one pop a vertex from S while S is not empty. Let the popped vertex be ‘v’. Take v as source and do DFS (call DFSUtil(v)). The DFS starting from v prints strongly connected component of v. In the above example, we process vertices in order 0, 3, 4, 2, 1 (One by one popped from stack).

How does this work?

The above algorithm is DFS based. It does DFS two times. DFS of a graph produces a single tree if all vertices are reachable from the DFS starting point. Otherwise DFS produces a forest. So DFS of a graph with only one SCC always produces a tree. The important point to note is DFS may produce a tree or a forest when there are more than one SCCs depending upon the chosen starting point. For example, in the above diagram, if we start DFS from vertices 0 or 1 or 2, we get a tree as output. And if we start from 3 or 4, we get a forest. To find and print all SCCs, we would want to start DFS from vertex 4 (which is a sink vertex), then move to 3 which is sink in the remaining set (set excluding 4) and finally any of the remaining vertices (0, 1, 2). So how do we find this sequence of picking vertices as starting points of DFS? Unfortunately, there is no direct way for getting this sequence. However, if we do a DFS of graph and store vertices according to their finish times, we make sure that the finish time of a vertex that connects to other SCCs (other that its own SCC), will always be greater than finish time of vertices in the other SCC (See this for proof). For example, in DFS of above example graph, finish time of 0 is always greater than 3 and 4 (irrespective of the sequence of vertices considered for DFS). And finish time of 3 is always greater than 4. DFS doesn’t guarantee about other vertices, for example finish times of 1 and 2 may be smaller or greater than 3 and 4 depending upon the sequence of vertices considered for DFS. So to use this property, we do DFS traversal of complete graph and push every finished vertex to a stack. In stack, 3 always appears after 4, and 0 appear after both 3 and 4.
In the next step, we reverse the graph. Consider the graph of SCCs. In the reversed graph, the edges that connect two components are reversed. So the SCC {0, 1, 2} becomes sink and the SCC {4} becomes source. As discussed above, in stack, we always have 0 before 3 and 4. So if we do a DFS of the reversed graph using sequence of vertices in stack, we process vertices from sink to source (in reversed graph). That is what we wanted to achieve and that is all needed to print SCCs one by one.

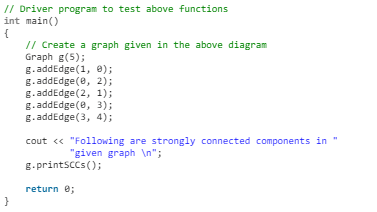
Following is C++ implementation of Kosaraju’s algorithm.

• C++
  
  
  
  
• Java
  
  
  
  
• Python
  
  
  

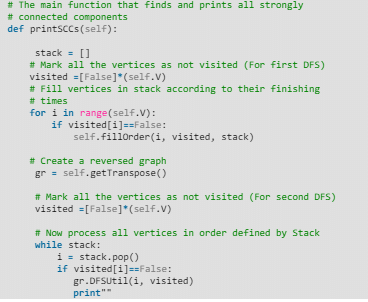
Output:
Following are strongly connected components in given graph
0 1 2
3
4
Time Complexity: The above algorithm calls DFS, finds reverse of the graph and again calls DFS. DFS takes O(V+E) for a graph represented using adjacency list. Reversing a graph also takes O(V+E) time. For reversing the graph, we simple traverse all adjacency lists.
The above algorithm is asymptotically best algorithm, but there are other algorithms like Tarjan’s algorithm and path-based which have same time complexity but find SCCs using single DFS. The Tarjan’s algorithm is discussed in the following post.