Properties of Triangles | Mathematics (Maths) Class 9 PDF Download
A Triangle is the simplest form of a Polygon. The word “Tri” means three and therefore a figure with 3 angles is a triangle, and It is formed with the help of three-line segments intersecting each other, a triangle has 3 vertices, 3 edges, and 3 angles. The shape of a triangle is very useful in real life too, like Carpenting, Astronomy, street signboards, etc.
There are several properties on triangles that justify a lot of applications and are useful for theorems.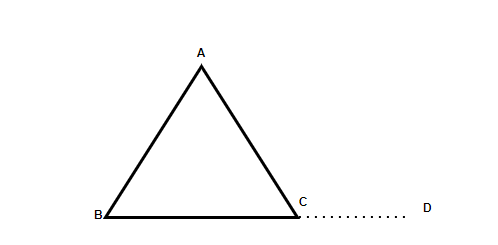
Properties of a Triangle
- Angle Sum Property: The sum of all three interior angles is always 180°. Therefore. In the Triangle ΔABC shown above, ∠A+ ∠B+ ∠C= 180°, interior angles of a triangle will be greater than 0° and less than 180°.
- A Triangle has 3 sides, 3 vertices, and 3 angles.
- Exterior angle property: The Exterior angle of a triangle is equal to the sum of Interior opposite and non-adjacent angles (also referred to as remote interior angles). In the above shown ΔABC, ∠ACD= ∠ABC+ ∠BAC
- The sum of the length of any two sides of a triangle is always greater than the third side. For example, AB+ BC> AC or BC+ AC> AB.
- The side opposite to the largest angle is the largest side of the triangle. For instance, in a right-angled triangle, the side opposite to 90° is the longest side.
- The perimeter of a figure is defined by the overall length the figure is covering. Hence, the perimeter of a triangle is equal to the sum of lengths all three sides of the triangle. Perimeter of ΔABC= (AB + BC + AC)
- The difference between the length of any two sides is always lesser than the third side. For example, AB-BC< AC or BC-AC< AB
- For similar triangles, the angles of the two triangles have to be congruent to each other and the respective sides should be proportional.
- Area of Triangle: 1/2× base × height
Classification of triangles
Classification of triangles is done based on the following characteristics:
- Based on the characteristics of sides.
- Based on the characteristics of angles.
Classification of Triangles based on Sides
Equilateral Triangle
In an Equilateral triangle, all three sides are equal to each other as well as all three interior angles of the equilateral triangle are equal.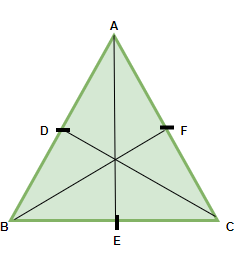
Since all the interior angles are equal and the sum of all the interior angles of a triangle is 180° (one of the Properties of Triangle). We can calculate the individual angles of an equilateral triangle.
∠A+ ∠B+ ∠C = 180°
∠A = ∠B = ∠C
Therefore, 3∠A = 180°
∠A= 180/3 = 60°
Hence, ∠A = ∠B = ∠C = 60°
Properties of Equilateral Triangle
- All sides are equal.
- All angles are equal and are equal to 60°
- There exist three lines of symmetry in an equilateral triangle
- The angular bisector, altitude, median, and perpendicular line are all same and here it is AE.
- The orthocentre and centroid are the same.
Isosceles Triangle
In an Isosceles triangle, two sides are equal and the two angles opposite to the sides are also equal. It can be said that any two sides are always congruent.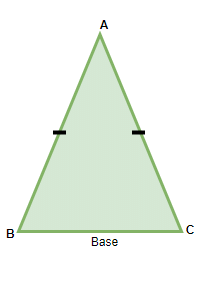
Properties of Isosceles Triangle
- Two sides of the isosceles triangle are always equal
- The third side is referred to as the base of the triangle and the height is calculated from the base to the opposite vertex
- The opposite angles of the two equal sides are also equal to each other.
Scalene Triangle
In a Scalene triangle, all sides and all angles are unequal. Imagine drawing a triangle randomly and none of its sides are equal, all angles differ from each other too.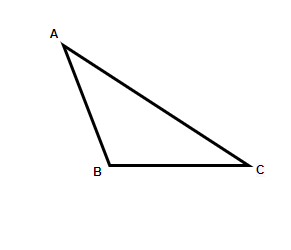
Properties of Scalene Triangle
- None of the sides are equal to each other.
- The interior angles of the scalene triangle are all different.
- No line of symmetry exists.
- No point of symmetry can be seen.
- The interior angles may be acute, obtuse, or right angle in nature (this is the classification based on angles).
- The smallest side is opposite to the smallest angle and the largest side is opposite to the largest angle (general property).
Classification of triangles based on angles
Acute angle Triangle
In Acute angle triangles, all the angles are greater than 0° and less than 90°. So, it can be said that all 3 angles are acute in nature (angles are lesser than 90°)
Properties of acute angle triangles
- All the interior angles are always less than 90° with different lengths of their sides.
- The line that goes from base to the opposite vertex is always perpendicular.
Obtuse angle Triangle
In an obtuse angle Triangle, one of the 3 sides will always be greater than 90° and since the sum of all the three sides is 180°, the rest of the two sides will be less than 90°(angle sum property).
Properties of obtuse angle triangle
- One of the three angles is always greater than 90°.
- The sum of the remaining two angles is always less than 90° (angle sum property).
- The circumference and the orthocentre of the obtuse angle lie outside the triangle.
- The Incentre and the centroid lie inside the triangle.
Right angle Triangle
When one angle of a triangle is exactly 90°, then the triangle is known as the Right Angle Triangle.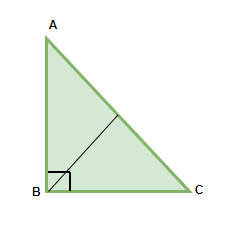
Properties of Right-angled Triangle
- A Right-angled Triangle must have one angle exactly equal to 90°, it may be scalene or isosceles but since one angle has to be 90°, hence, it can never be an equilateral triangle.
- The side opposite to 90° is called Hypotenuse.
- The sides adjacent to the 90° are base and perpendicular.
- Pythagoras Theorem: It is a special property for Right-angled triangles. It states that the square of the hypotenuse is equal to the sum of the squares of base and perpendicular i.e. AC2 = AB2 + BC2
Sample Problems on Properties of Triangles
Question 1: In the triangle. ∠ACD = 120°, and ∠ABC = 60°. Find the type of the Triangle.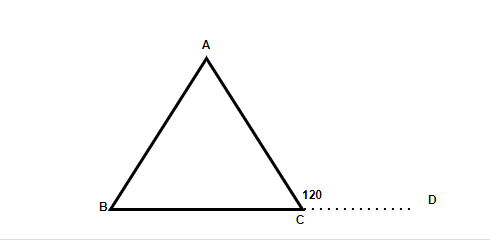
Solution:
In the above figure, we can say, ∠ACD = ∠ABC + ∠BAC (Exterior angle Property)
120° = 60° + ∠BAC
∠BAC = 60°
∠A + ∠B + ∠C = 180°
∠C OR ∠ACB = 60°
Since all the three angles are 60°, the triangle is an Equilateral Triangle.
Question 2: The Triangle in the figure given below has the lengths of its sides as mentioned. Find the area and perimeter of the Triangle.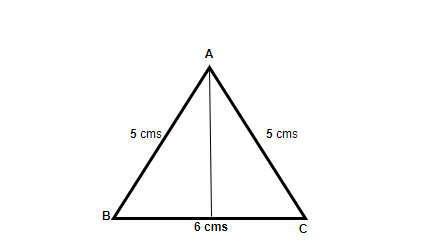
Solution:
In the figure shown, we know the length of all the sides and therefore,
The perimeter of the triangle = (5 + 5 + 6) = 16cms
In order to find the area of the triangle, we need to find out the height of the triangle.
Applying Pythagoras to find out the height of the triangle,
H2 = (52– 32) = 16
H = 4cms
Therefore, the area of Triangle ABC = 1/2 × 4 × 5 = 10cm2
Question 3: Explain why a Right-angled Triangle can never be Equilateral in nature?
Solution:
A Right angled Triangle has one of its angles equal to 90°, and the rest of the angles are less than 90° [since the sum of all angles of a triangle is 180]. While in an equilateral triangle, all the interior angles are equal and are equal to 60° which is not possible for a right-angled triangle.
Even if an angle is considered to be 60°, since one angle is already 90°, the third will become 30°.
Therefore, it is not possible for an equilateral triangle to be a right-angled triangle.
Question 4: In the Right-angled triangle, ∠ACB = 60°, and the length of the base is given as 4cm. Find the area of the Triangle.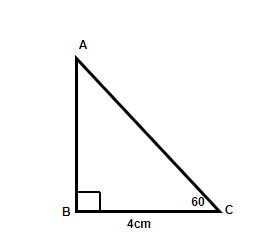
Solution:
Using Trigonometric formula of Tan60°,
Tan60° = AB/BC = AB/4
AB = 4√3cm
Area of Triangle ABC = 1/2 = 1/2×4×4√3 = 8√3cm2
Question 5: In ΔABC if ∠A+ ∠B = 55°. ∠B + ∠C = 150°, Find angle B separately?
Solution:
The angle sum Property of a Triangle says ∠A+ ∠B+ ∠C= 180°
Given: ∠A+ ∠B = 55°
∠B+ ∠C = 150°
Adding the above 2 equations,
∠A+ ∠B+ ∠B+ ∠C = 205°
180°+ ∠B = 205°
∠B = 25°
|
40 videos|563 docs|57 tests
|
FAQs on Properties of Triangles - Mathematics (Maths) Class 9
| 1. What are the three sides of a triangle called? |  |
| 2. How many types of triangles are there based on their angles? |  |
| 3. What is the sum of the angles in a triangle? |  |
| 4. How can we determine if a triangle is equilateral? |  |
| 5. Can a triangle have two right angles? |  |






















