Motion in Combined Electric & Magnetic Fields | Physics for JAMB PDF Download
It has long been known that charged particles move in circular orbits in the magnetic field. The Van Allen radiation belts in space around the earth consist of these energetic charges trapped in the magnetic field of the earth. But what is a magnetic field? Magnetic fields are also used to guide the motion of charged particles in accelerators for both research and medical purposes. The orbiting motion of charges in a magnetic field is the basis for measuring the mass of an atom.
Lorentz Force
Lorentz force is the force exerted on a charged particle moving through both electric and magnetic field.
F = qE + qv × B ……….(1)
where,
F = Lorentz Force
q = Charge on the Particle
E = Electric Field
B = Magnetic Field
v = Velocity of the Particle
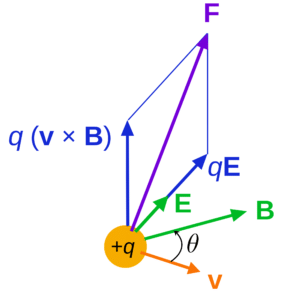 Lorentz Force
Lorentz Force
In a vacuum where collisions between particles are not very frequent, a particle with charge q, mass m, and velocity v perpendicular to a uniform magnetic field B (no E) moves in a circular path with the radius
r = mv / qB ………..(2)
One can also deflect the trajectory of a charged particle with an electric field, although not into a circular path. If the electric force on the particle is both equal and opposite to the magnetic force, the net force on the particle will be zero. From Eq. (1), this will happen if
v=E / B ……….(3)
The motion of a charged particle in the electric and magnetic field
In case of motion of a charge in a magnetic field, the magnetic force is perpendicular to the velocity of the particle. So no work is done and no change in the magnitude of the velocity is produced (though the direction of momentum may be changed). We shall consider the motion of a charged particle in a uniform magnetic field. First, consider the case of v perpendicular to B.
The perpendicular force, q v × B, acts as a centripetal force and produces a circular motion perpendicular to the magnetic field. If velocity has a component along B, this component remains unchanged as the motion along the magnetic field will not be affected by the magnetic field.
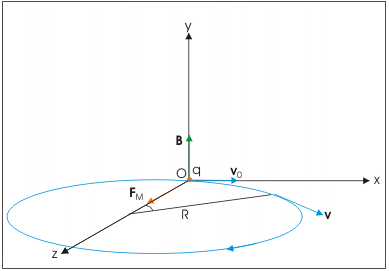 The circular motion of a charged particle in the magnetic field
The circular motion of a charged particle in the magnetic field
The motion in a plane perpendicular to B is as before a circular one, thereby producing a helical motion. However, the electric field in y-direction imparts acceleration in that direction. The particle, therefore, acquires velocity in the y-direction and resulting motion is a helical motion.
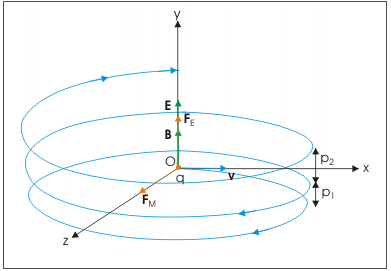 The motion of a charged particle in both electric and magnetic fields. Resulting motion is a helical motion with increasing pitch
The motion of a charged particle in both electric and magnetic fields. Resulting motion is a helical motion with increasing pitch
The radius of each of the circular element and other periodic attributes like time period, frequency and angular frequency is same as for the case of circular motion of a charged particle in perpendicular to magnetic field.
R = ν / αB
T = 2π / αB
ν = αB / 2π
ω = αB
If there is a component of the velocity parallel to the magnetic field (denoted by v2), it will make the particle move along both the field and the path of the particle would be a helical one. The distance moved along the magnetic field in one rotation is called pitch p.
p = v2T = 2πmv2 /qB
Applications
Some of the important applications associated with the presence of the two fields include:
- The motion of a charged particle in electric and magnetic fields
- Measurement of specific charge of an electron (J. J. Thomson experiment)
- Acceleration of charged particles (cyclotron)
Solved Examples
Ques: A charged particle moves in a gravity-free space without the change in velocity. Which of the following is/are possible?
A) B = 0, E = 0
B) E = 0, B ≠ 0
C) E ≠ 0, B = 0
D) B ≠ 0, E ≠ 0
Ans: If A charged particle moves in a gravity-free space without a change in velocity, then
- Particle can move with constant velocity in any direction. So B =0, E = 0
- Particle can move in a circle with constant speed. Magnetic force will provide the centripetal force that causes particle to move in a circle.
- If qE = qvB and Magnetic & Electric force in opposite direction in this case also particle move with uniform speed.
|
263 videos|277 docs|238 tests
|
FAQs on Motion in Combined Electric & Magnetic Fields - Physics for JAMB
| 1. What is the motion in combined electric and magnetic fields? |  |
| 2. How do electric and magnetic fields interact to affect the motion of charged particles? |  |
| 3. What is the relationship between the velocity of charged particles and the resulting path in combined electric and magnetic fields? |  |
| 4. How does the magnitude of the electric and magnetic fields affect the motion of charged particles in combined fields? |  |
| 5. Can the motion of charged particles in combined electric and magnetic fields be controlled or manipulated? |  |
















