Projectile Motion | Physics Class 11 - NEET PDF Download
You must be aware of the 87.58 m long, mighty throw of the javelin by Neeraj Chopra in the Olympics. How did he do it so well? Well, the answer is physics! Throwing the javelin at a certain fixed angle and velocity will let it fly at the maximum distance. Sounds interesting!
An object like a javelin thrown in the air is called a projectile. A projectile is an object flying through the air under the effect of gravity. Through this document, we will understand in detail projectile motion and the math behind it.
 Javelin Throw
Javelin Throw
What is Projectile Motion?
When a particle is thrown at an angle near the earth’s surface, it moves along a curved path under the effect of gravity. The path of such a particle is called a projectile and the motion is called projectile motion. The path followed by the projectile is called its trajectory.
Some examples of projectile are:
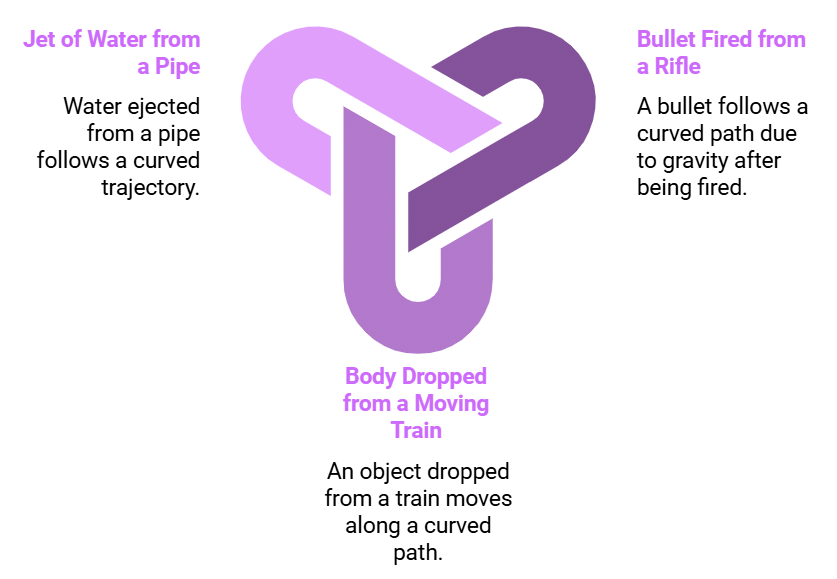
Types of Projectiles
- Horizontal projectile: In this, the body is given an initial velocity directed along the horizontal and then it moves under the influence of gravity along a parabolic path.
- Oblique projectile: In this, the body is given an initial velocity making an angle with the horizontal and it moves under the influence of gravity along a parabolic path.
- Projectile on an Inclined Plane: If the projectile motion is occurring on an inclined plane which is making some angle with the earth, then we call it projectile motion on an inclined plane.
 Types of Projectiles
Types of Projectiles
We will first understand the case of the Horizontal Projectile and then the Oblique projectile followed by the projectile on an inclined plane.
Assumptions in Projectile Motion
While studying projectile motion, we assume that-
- there is no air friction
- acceleration due to gravity is constant at all points during the motion of a projectile
- there is no effect of the rotation of the earth on the value of acceleration due to gravity
Components of Projectile Motion
In a Projectile Motion, there are two simultaneous independent motions:
- Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle.
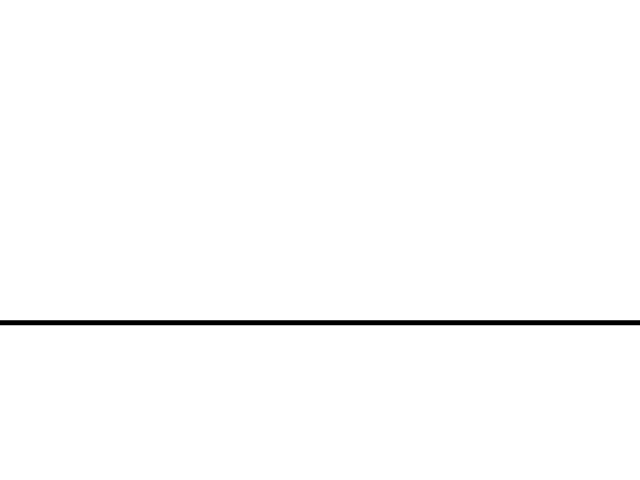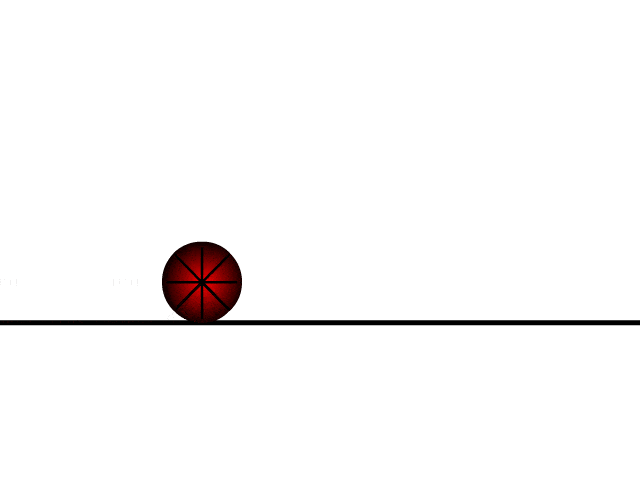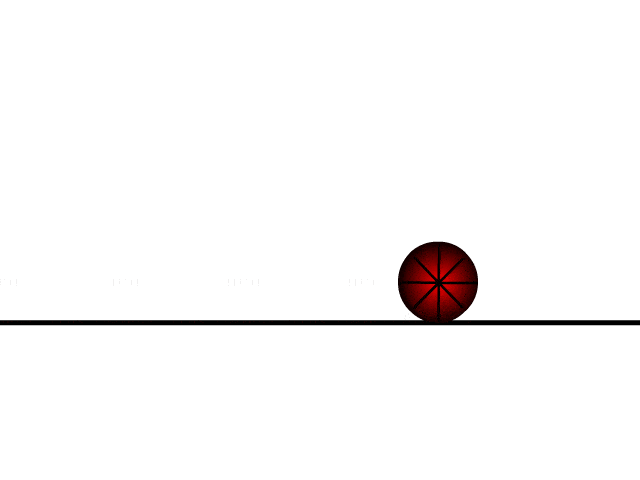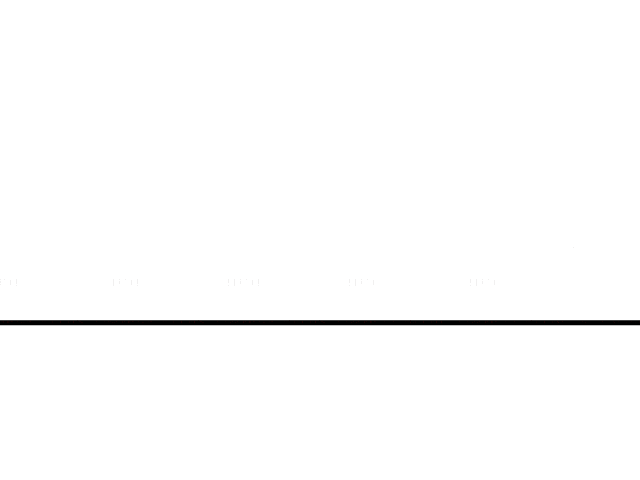 Motion along x-axis
Motion along x-axis - Along the y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle.
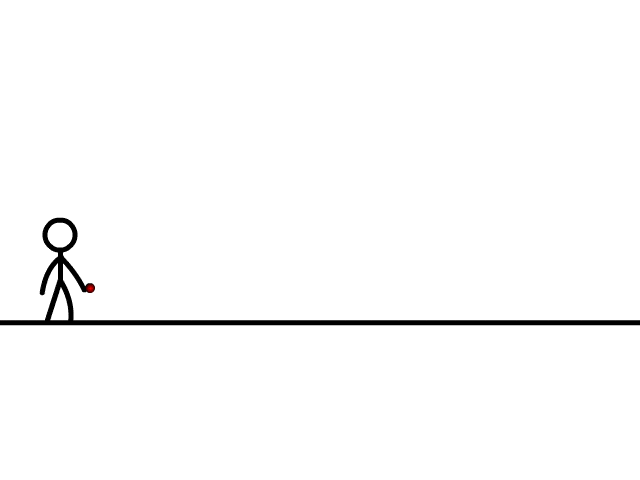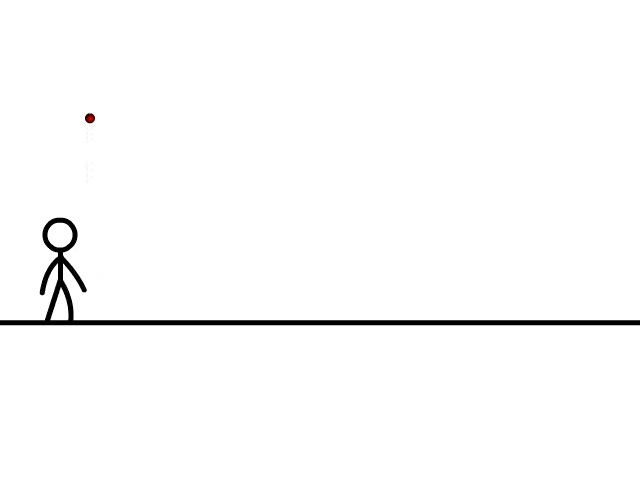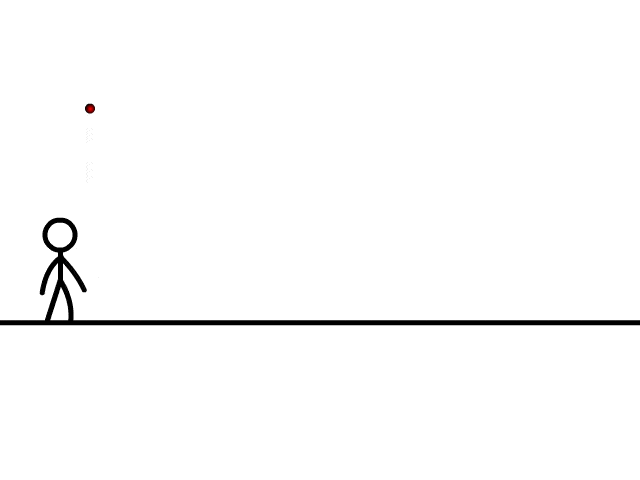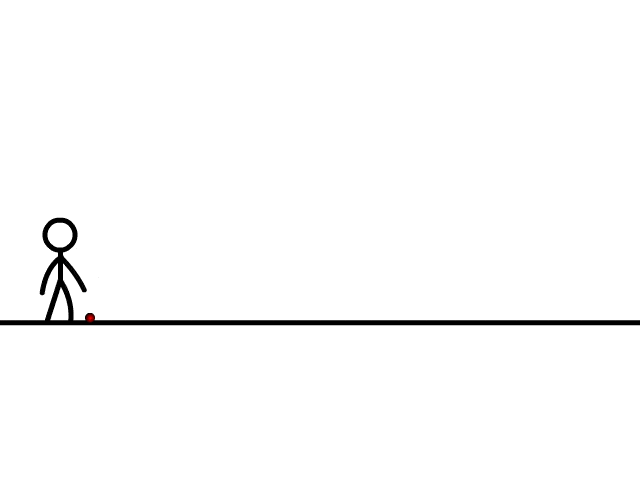 Motion along y-axis
Motion along y-axis
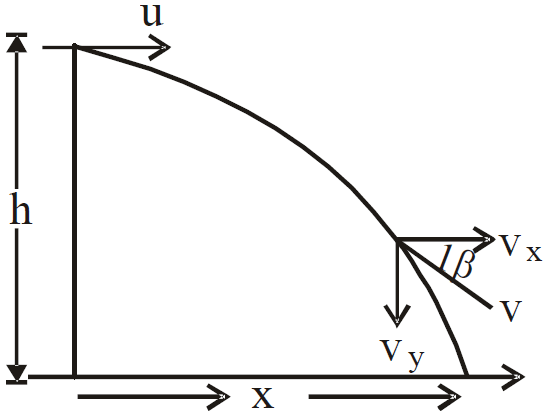
Horizontal Projectile
Let OX be a horizontal line parallel to the ground and OY is the vertical line perpendicular to the ground. Suppose an object is projected from point O above the ground with an initial velocity u along OX at time t=0. After the projection, the body will move under the effect of two independent perpendicular velocities.
- Horizontal Velocity u, which is constant throughout the motion
- Vertical Velocity which goes on increasing as the object descends due to gravity.
(A) Equation of Trajectory


Put the value of t from (1) in (2) you get,
y = 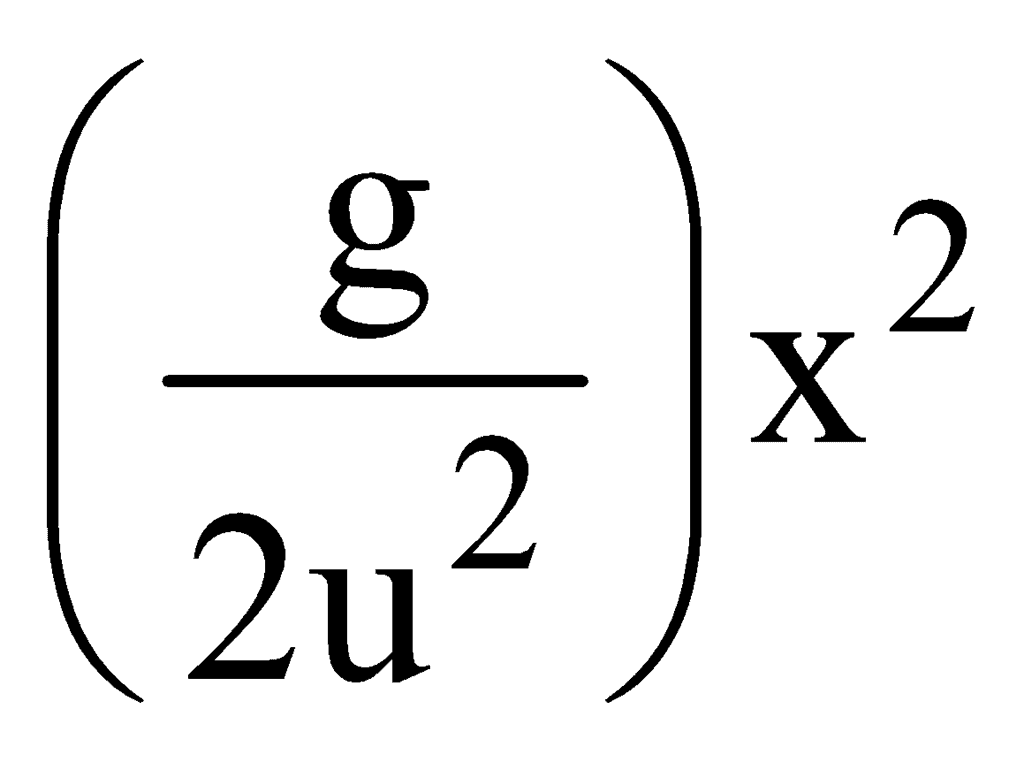 which is the equation of a parabola (y=kx2).
which is the equation of a parabola (y=kx2).
here k= g/2u2 = constant
(B) Velocity at any Instant
- Horizontal velocity, which remains unchanged vx = u
- Vertical velocity vy = uy + ayt by putting uy = 0 and ay =g you get vy = gt
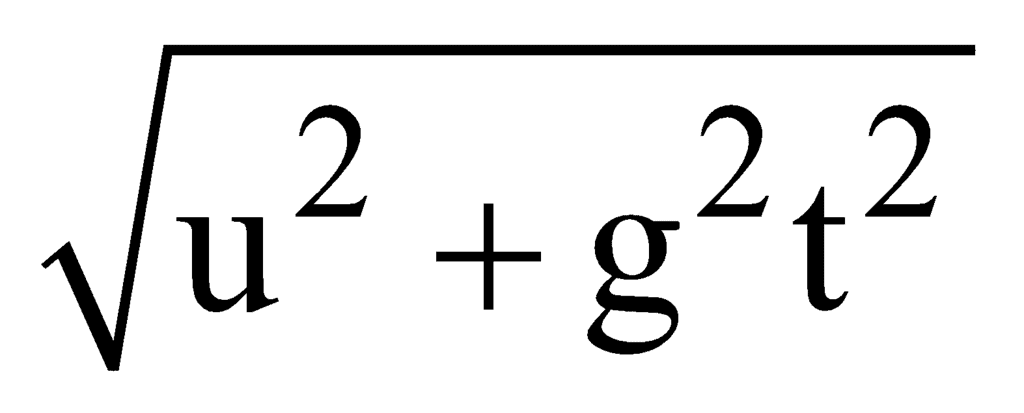
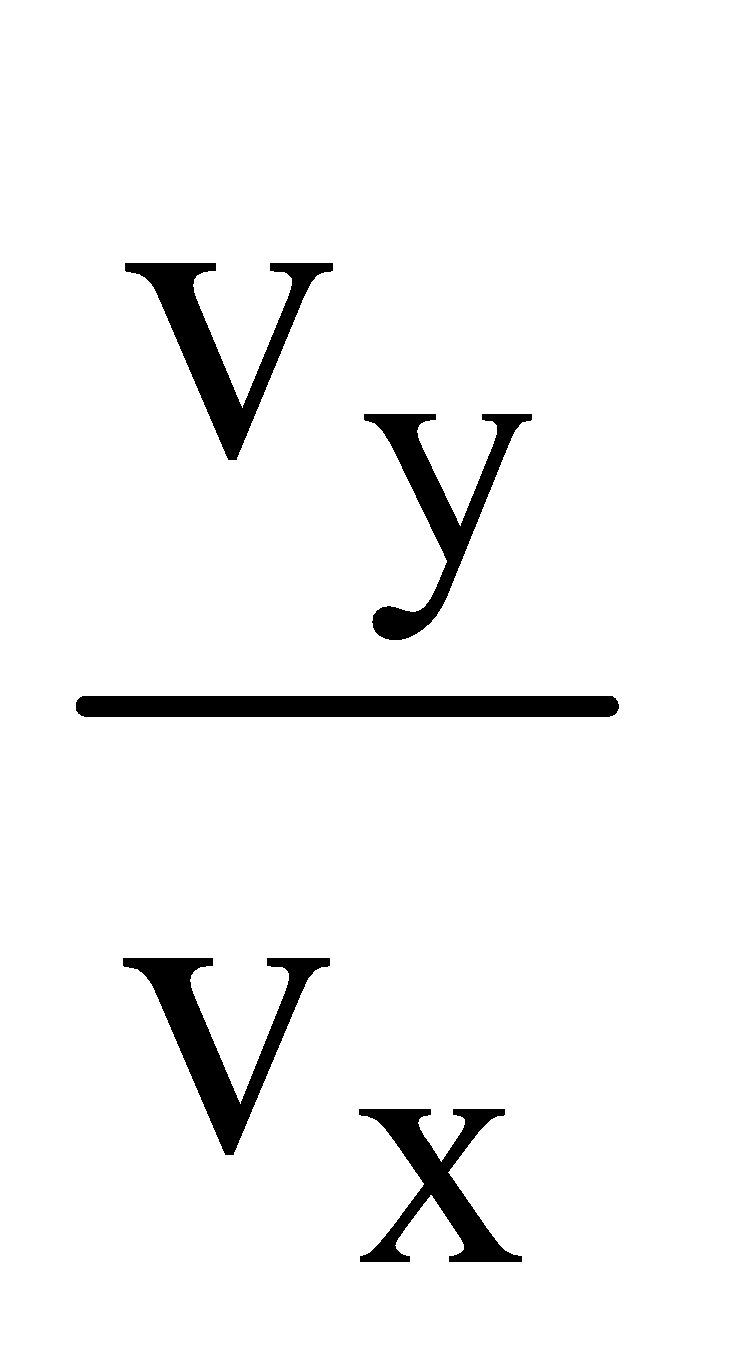 =
= 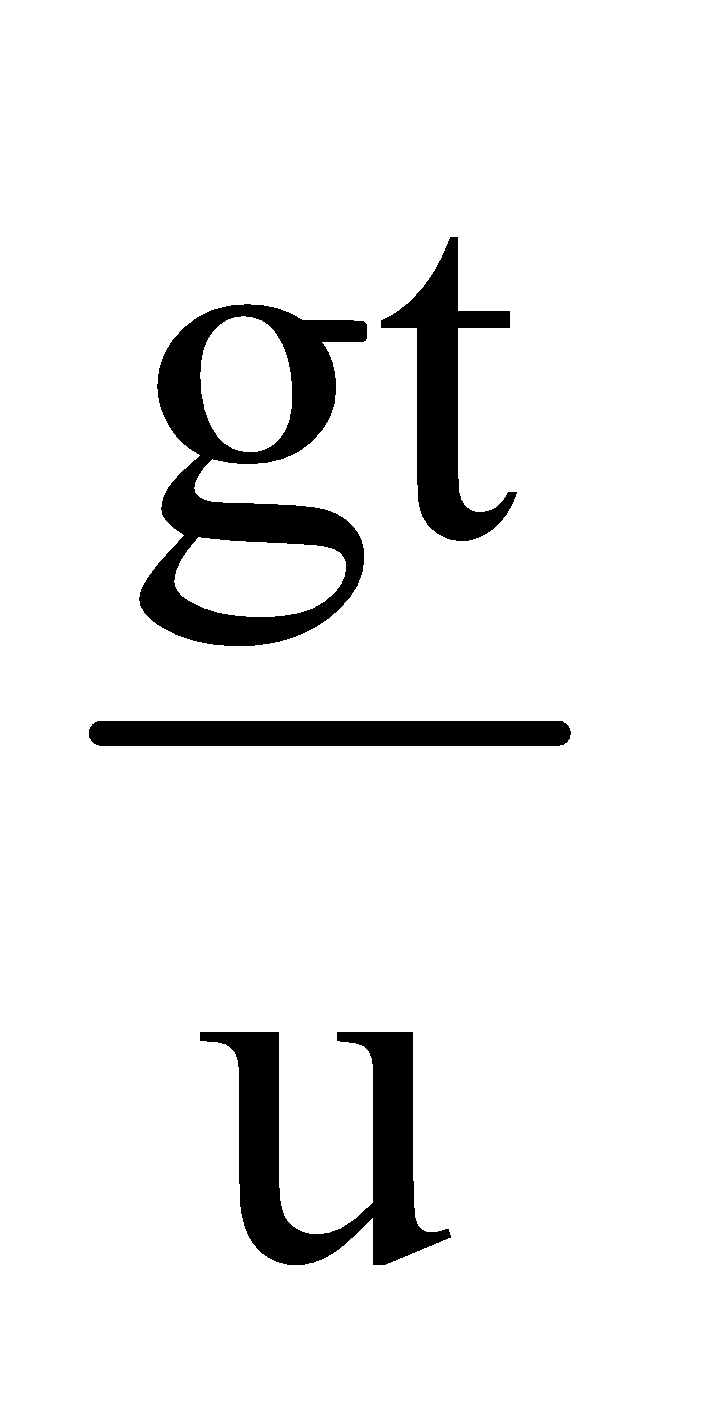
(C) Time of Flight
y=h, uy=0, ay=g, t=T so
h= 0xT+1/2gT2
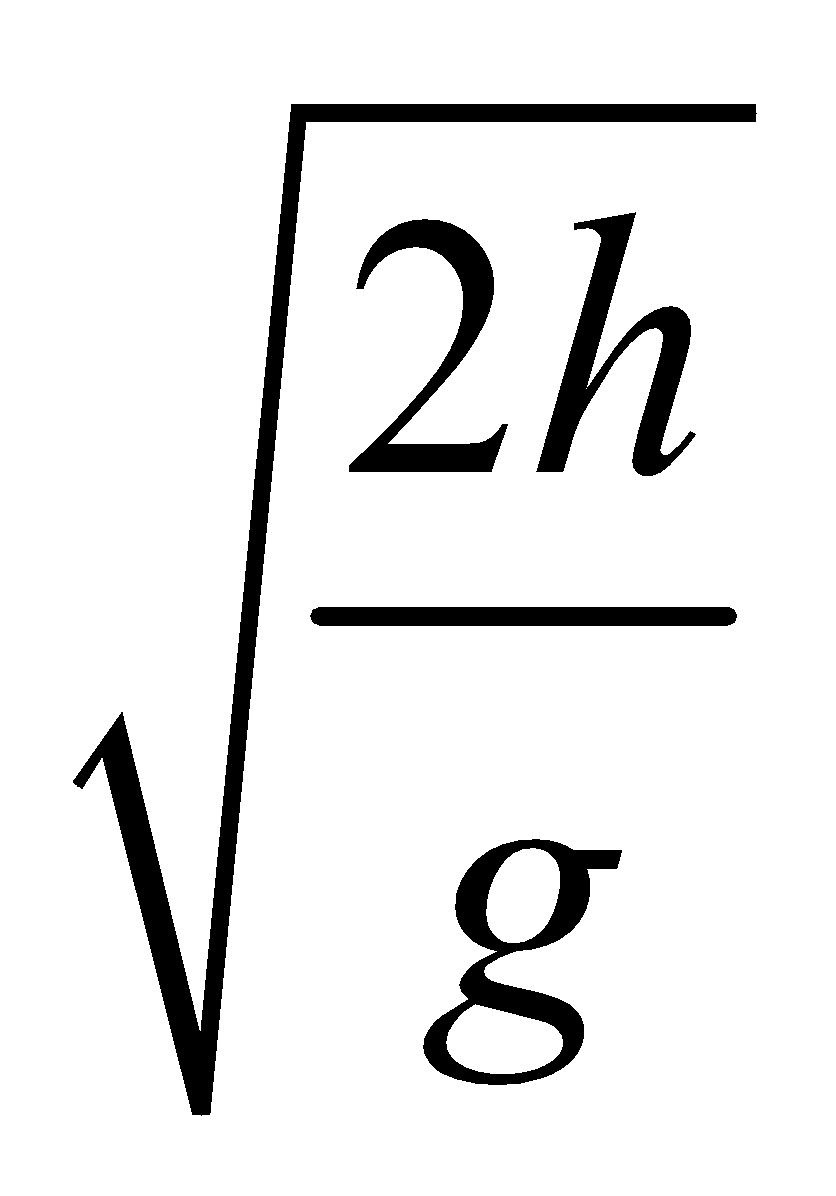 and
and 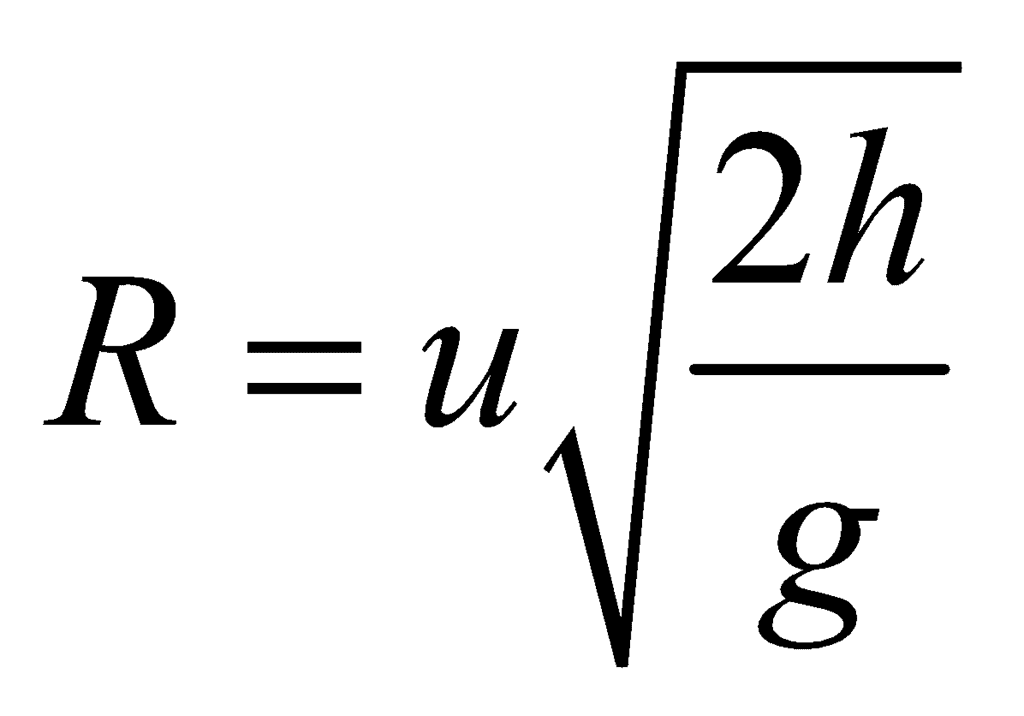
(D) Horizontal Range
Let R be the distance covered by the body in the x-direction. This is called as Horizontal Range.
x=R, ux=u, ax=0, t=T=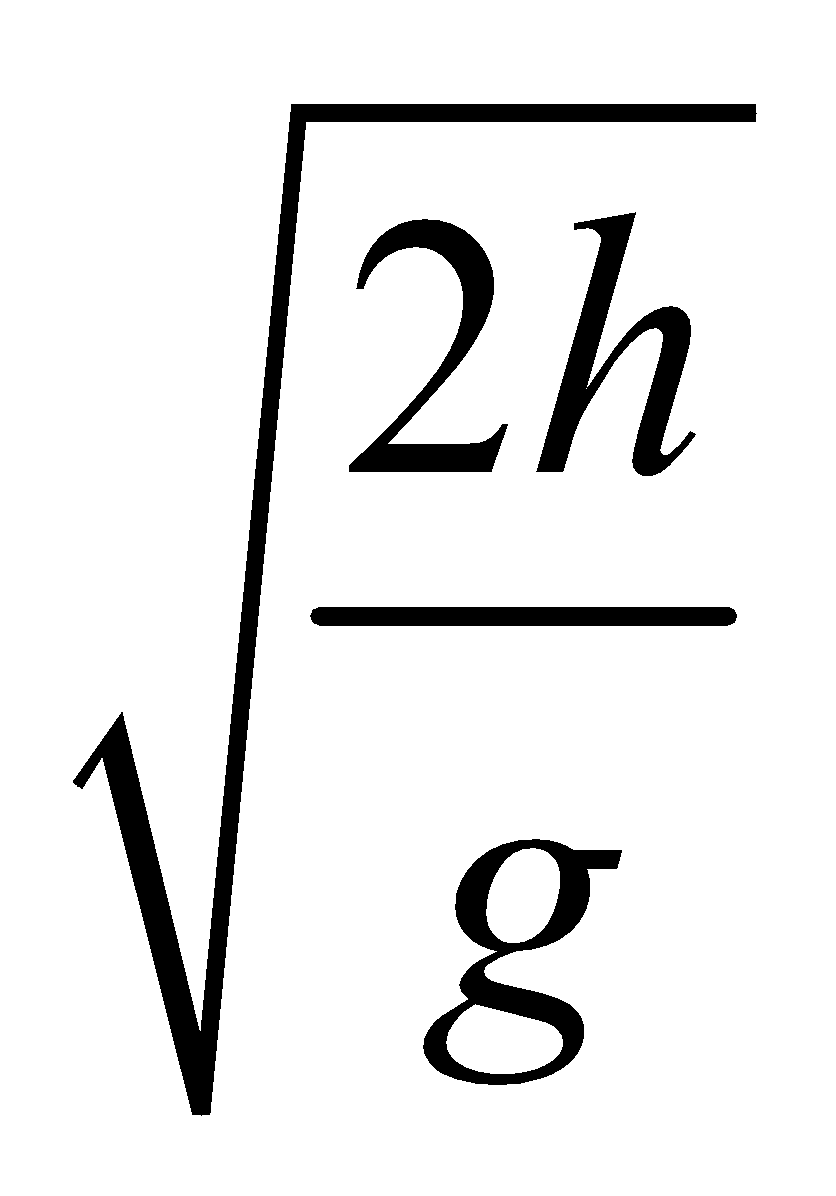
R= 0+ u + 1/2 x 0 x T2 = u
+ 1/2 x 0 x T2 = u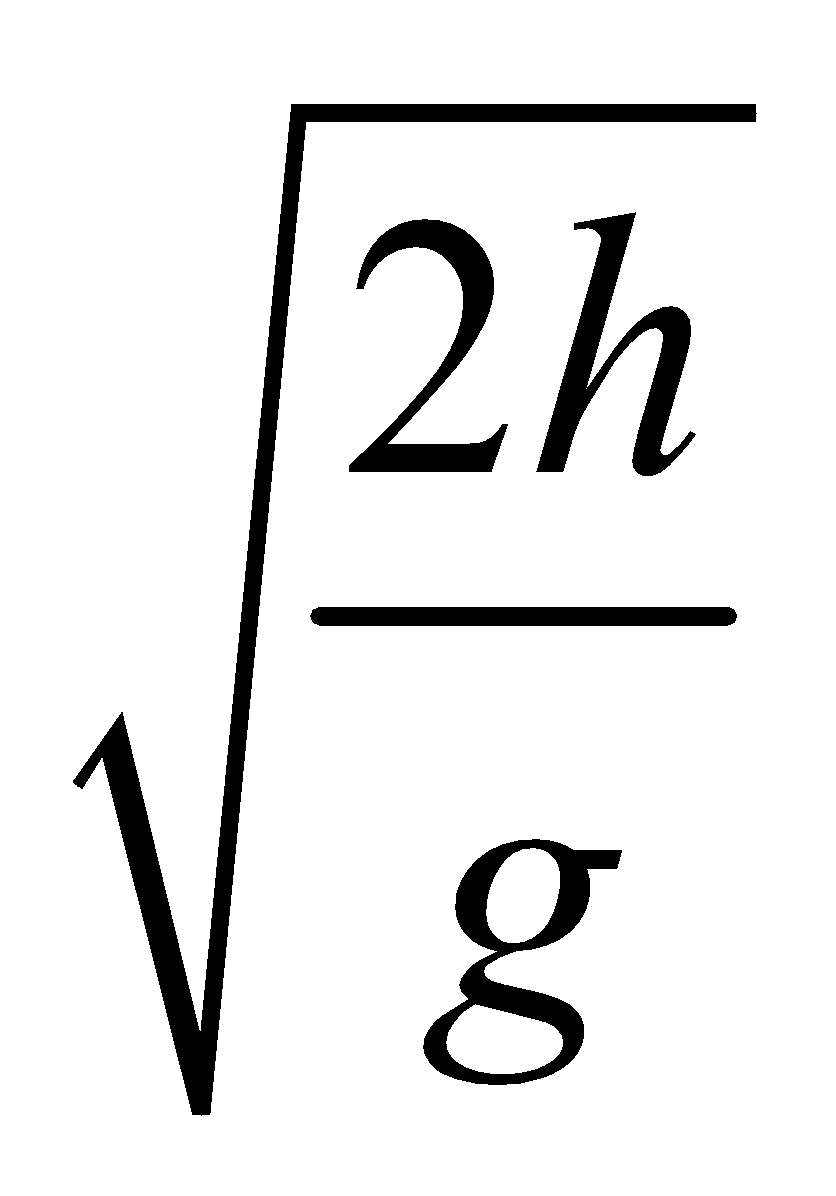
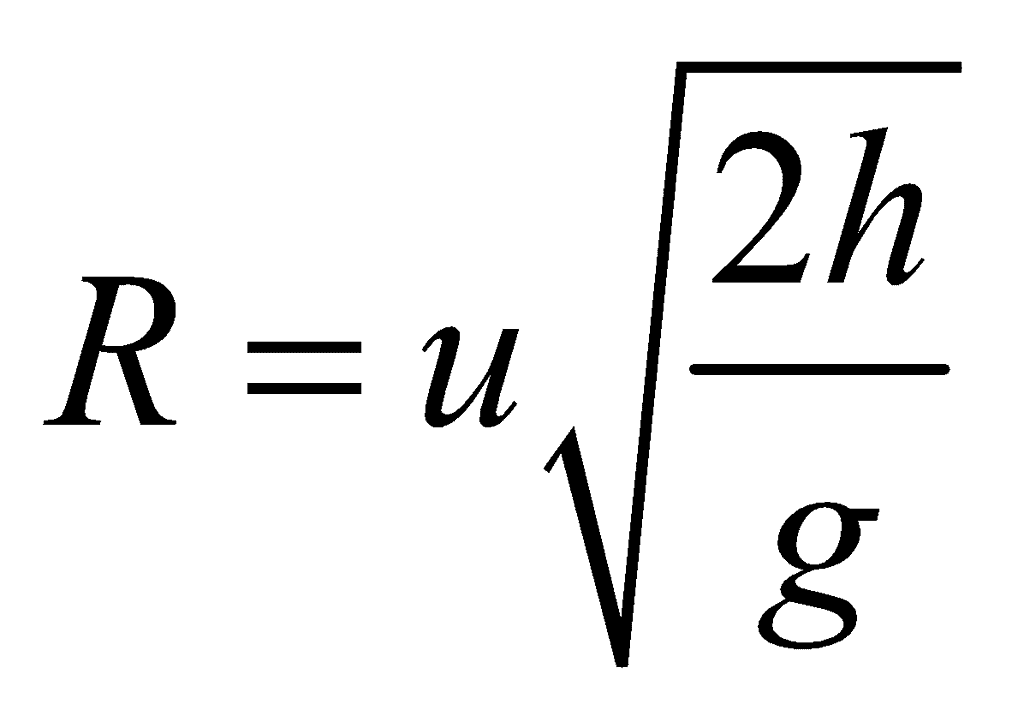
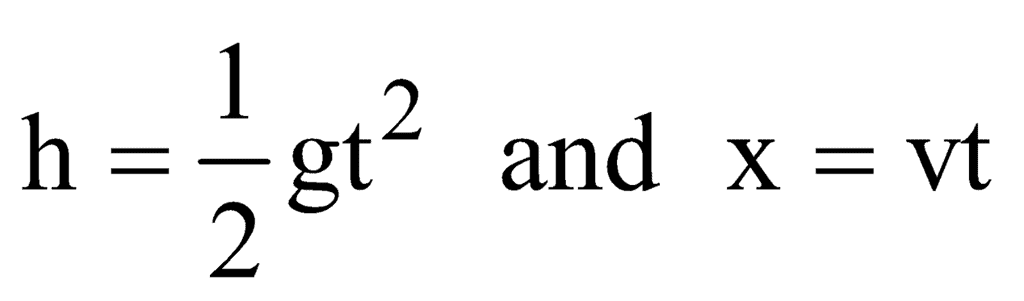
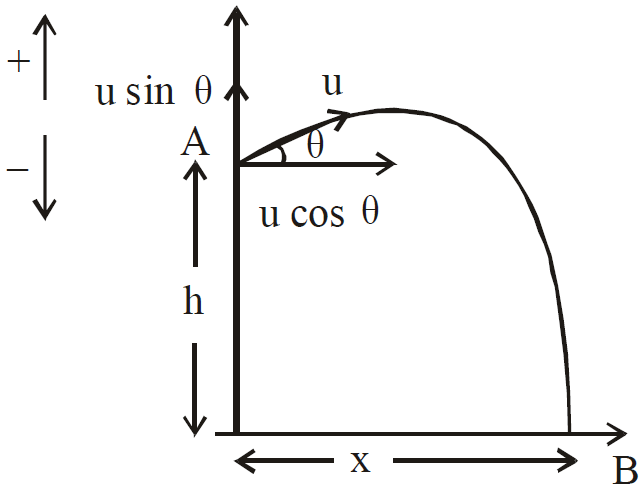
Case 2: If a particle is projected at an angle (θ) in an upward direction from the top of the tower of height h with velocity u, then
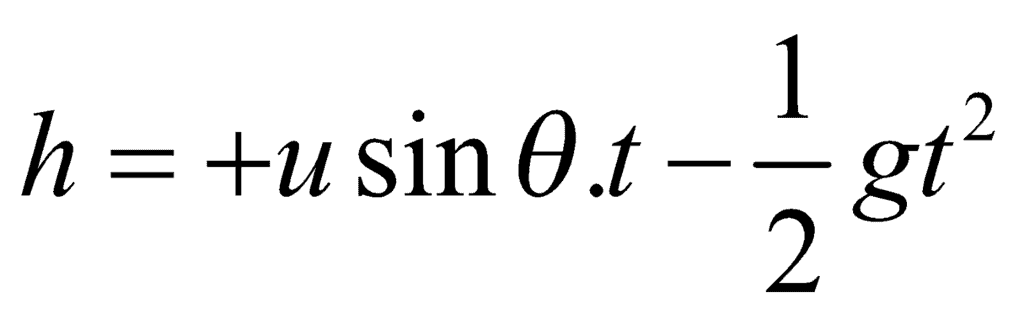 and x = u cosθ.t
and x = u cosθ.t
 Case 3: If a body is projected at an angle (θ) from the top of the tower in a downward direction then
Case 3: If a body is projected at an angle (θ) from the top of the tower in a downward direction then
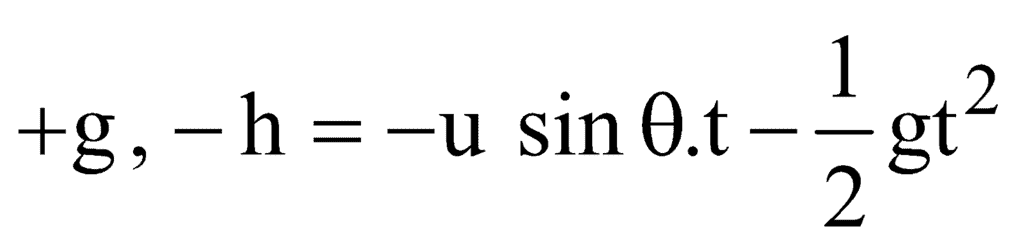 and x = u cosθ.t
and x = u cosθ.t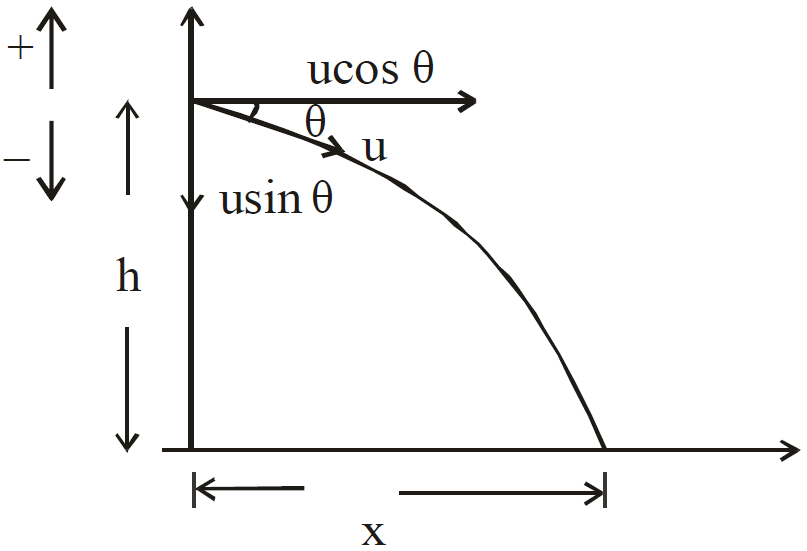
Oblique Projectile
(A) Equation of Trajectory
Let the point from which the projectile is thrown into space be taken as the origin, the horizontal direction in the plane of motion is taken as the X-axis, the vertical direction is taken as the Y-axis, Let the projectile be thrown with a velocity u making an angle θ with the X-axis.
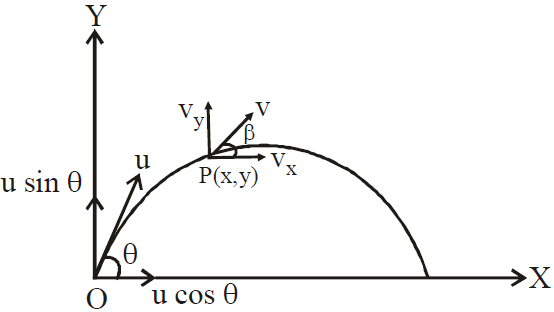

From equation (1) by putting the value of t, as a function of x, in equation (2), we get:
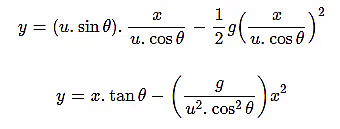
The above equation is called the equation of trajectory. As the equation represents a parabola (y=ax+bx2) , the trajectory (or the path) of a projectile is a parabola.
Tip: Here, u, θ, x, and y are four variables. If any three quantities, as mentioned, are known then the fourth quantity can be solved directly. There is another formula for the equation of trajectory, which is very important for competitive exams: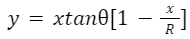
(B) Velocity at any Instant
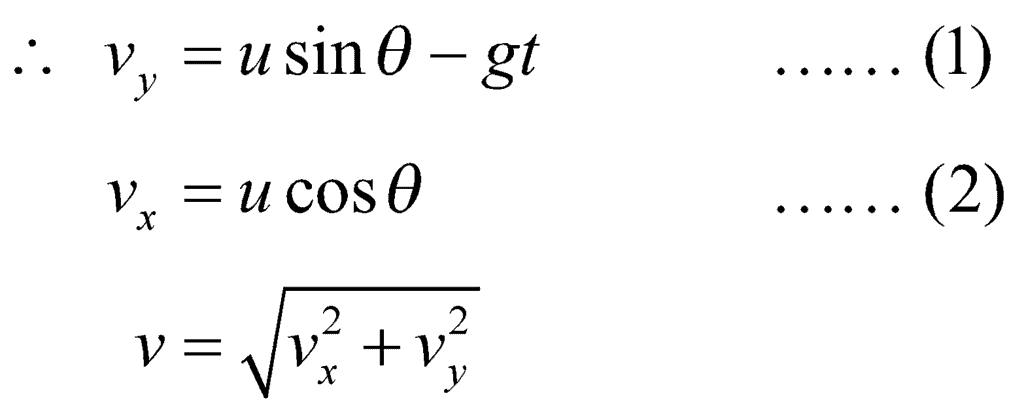
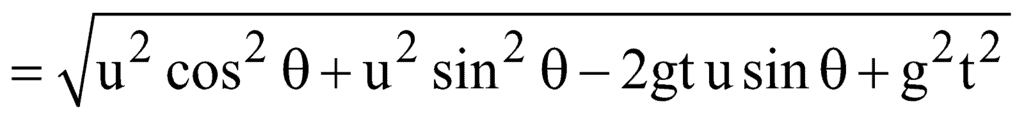
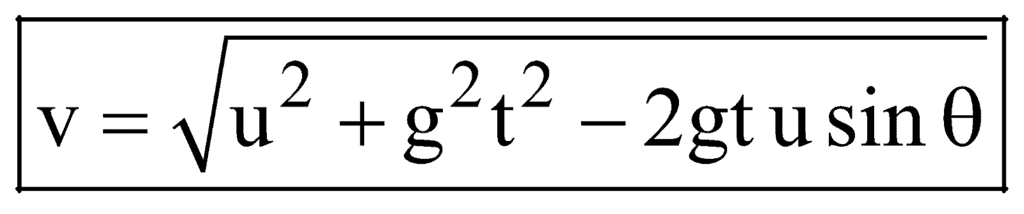
(C) Time of Flight
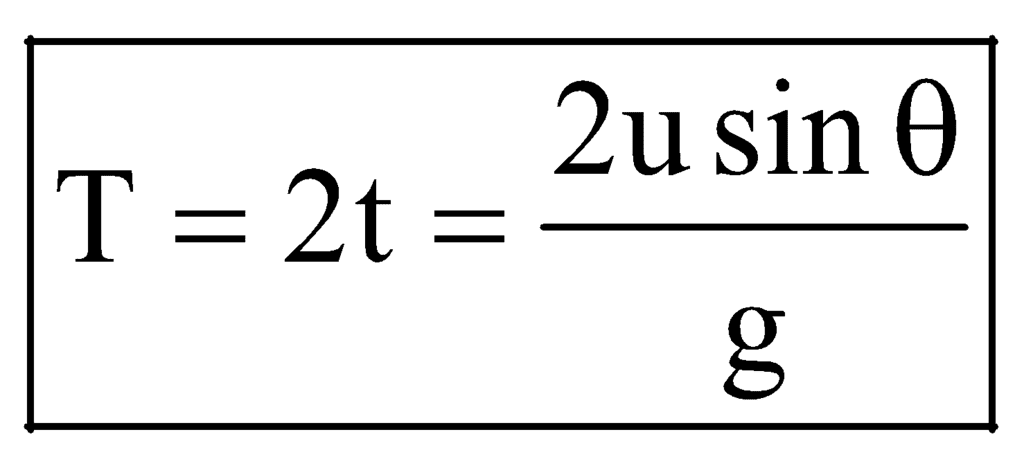
(D) Maximum Height
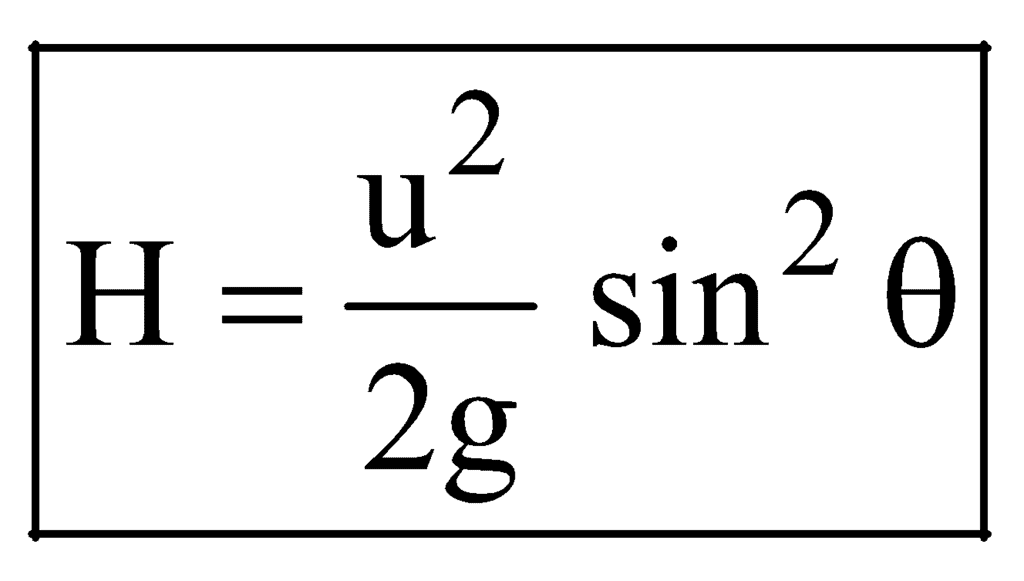
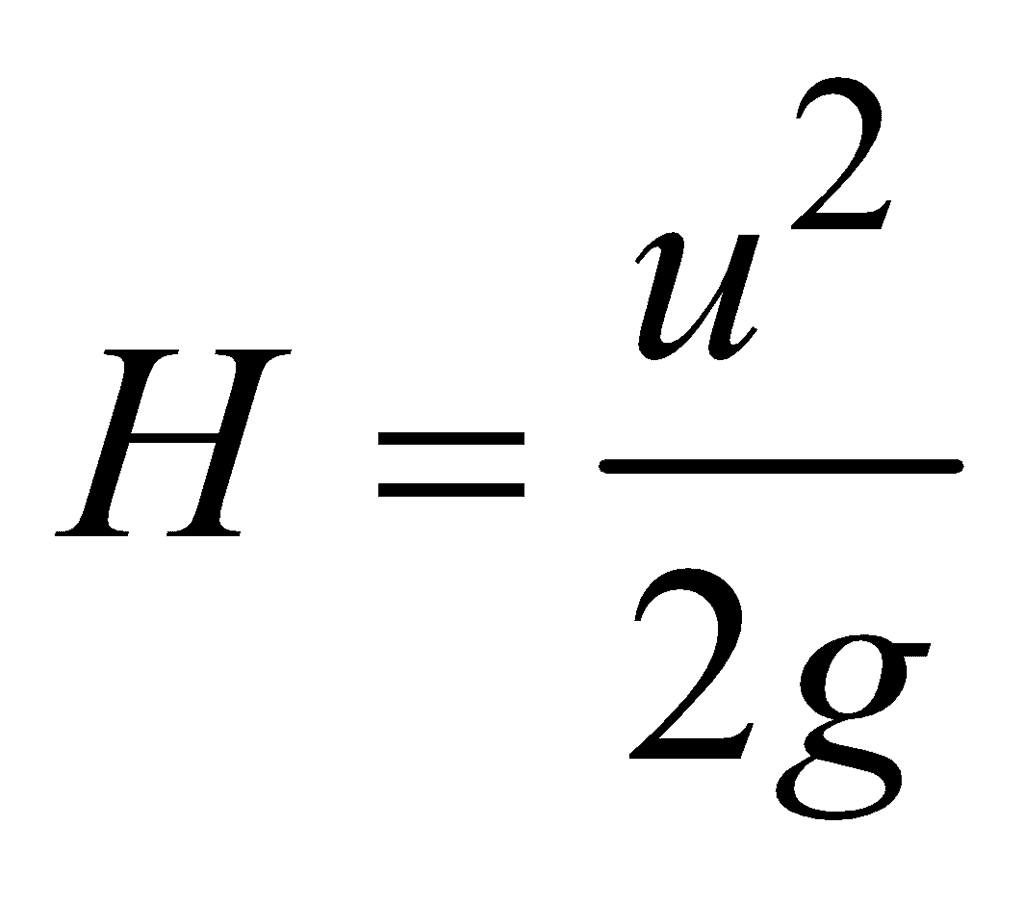
(E) Horizontal Range
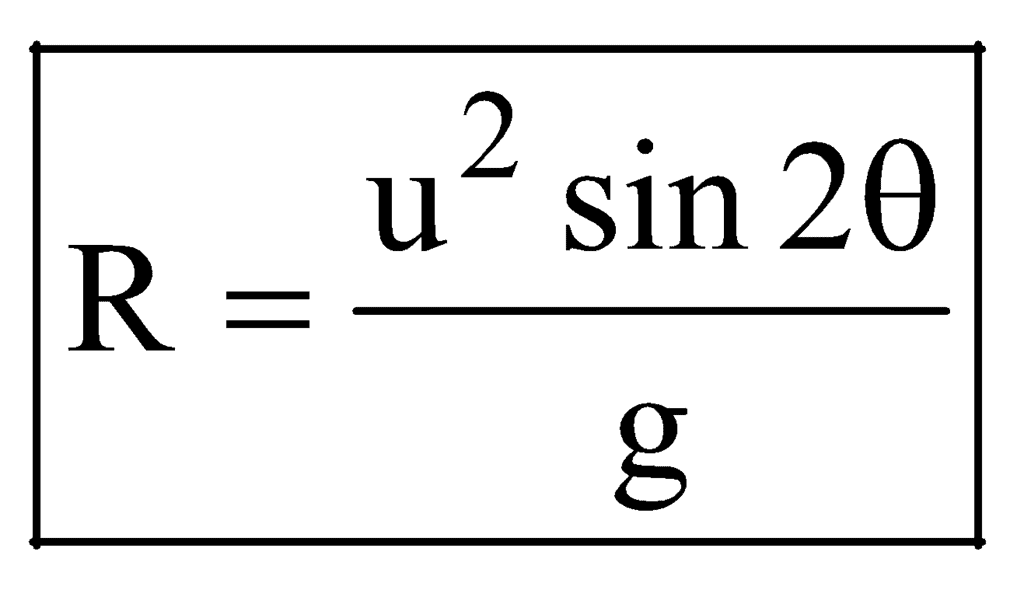 and
and 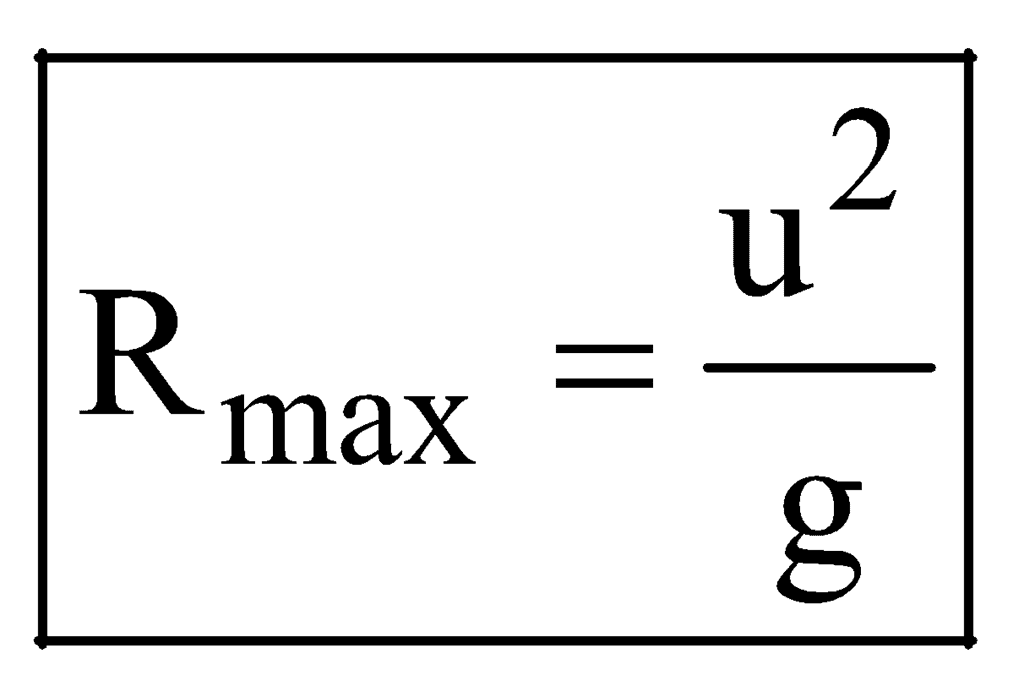 at θ = 45º (
at θ = 45º (  maximum value of sin2θ = 1)
maximum value of sin2θ = 1)Note that, the ratio of Rmax to Hmax is 2
So Rmax = 2Hmax
Relation between R, H, and T
Remember the relation:
R(tanθ) = 4H = 1/2g t2
The above formula is very useful for solving questions asked in competitions.
Complementary Angles in Projectile Motion
If two projectiles are launched at angles θ and 90- θ, which means, complementary angles (i.e. sum of the angles is 90 degrees) then the following results are important: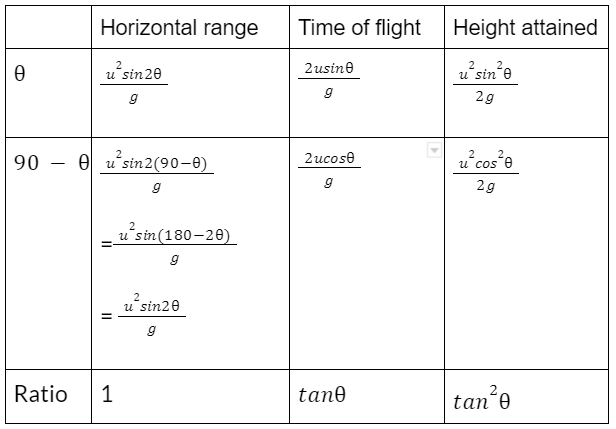
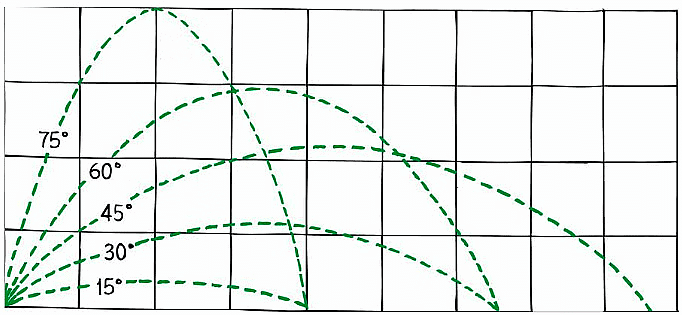
These results are important from competitive point of view: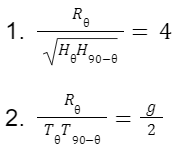
Example 1: A projectile thrown at 37o to the vertical. What is the angle of elevation of the highest point of the projectile from the point of projection?
Solution: 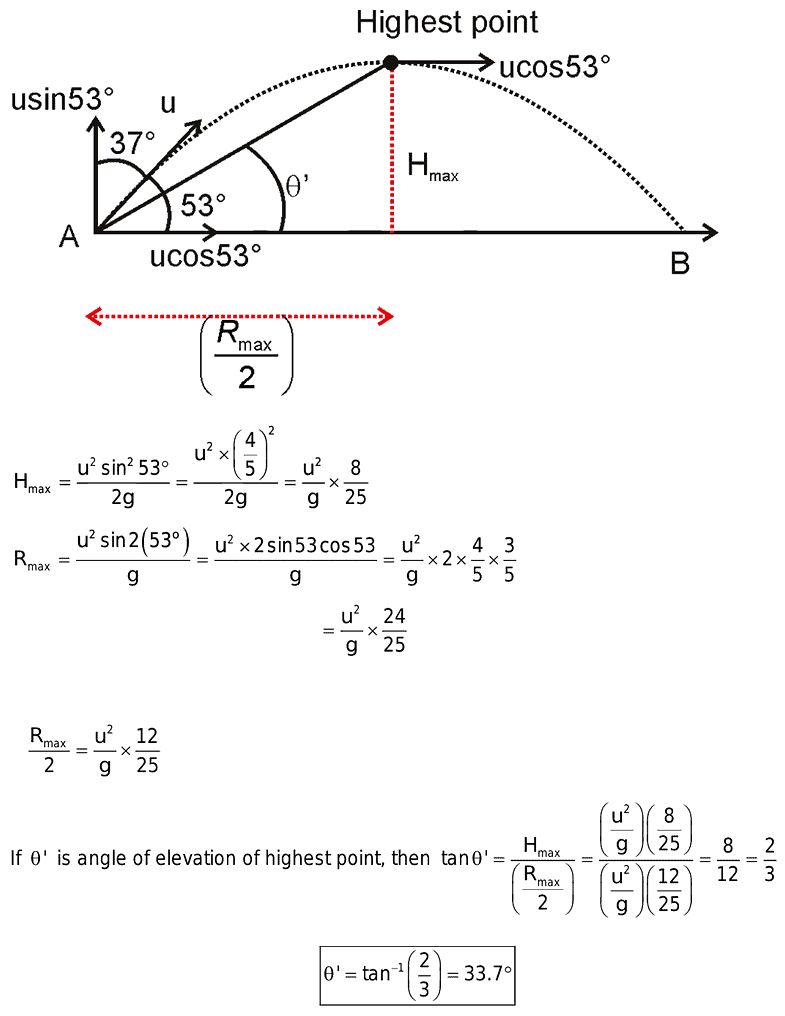
Example 2: A grasshopper can jump at a maximum horizontal distance of 50 cm. Find the maximum height of the stair step that the grasshopper can climb.
Solution: Since, Hmax/Rmax = 2
So Rmax = Hmax/2 = 50/2 = 25cm
Example 3: Marshall throws a ball at an angle of 600. If it moves at the rate of 6m/s and Steve catches it after 4s. Calculate the vertical distance covered by it.
Solution: Given,
0 = 60°
Initial velocity = vo = 6m/sec
time = 4 sec
The horizontal distance is given by:
x = vot
x = 6 m/sec x 4 sec
x = 24 m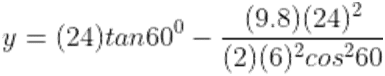
y = (24)(1.7320) – [ (9.8)(24)(24)/(2)(36)(0.25)]
y = 41.568 – [5644.8/18]
y= 41.568 – 313.6
y= – 272.032 m
Example 5: An object of mass 2000 g covers a maximum vertical distance of 6 m when it is projected at an angle of 45° from the ground. Calculate the velocity with which it was thrown. Take g = 10 m/s2,
(a) 12.10 m/s
(b) 15.49 m/s
(c) 2.155 m/s
(d) 12.0 m/s
Solution: Here, h = 6
θ = 45°
g = 10
h = (v sinθ) 2/2g is the formula for maximum height.
Solving the equation by substituting the values,
h= (v2*[sin(45°)]2)/(2*10)
h = v2X (1/√2 )2/20
6 = [v2X (1/2)]/20
6 X 20 X 2 = v2
240 = v2
v = 15.49
we get the initial velocity as 15.49 m/s.
Example 6: A body is projected with a velocity of 20ms−1 at 50° to the horizontal plane. Find the time of flight of the projectile.
Solution: Initial Velocity Vo = 20ms−1
And angle θ=50°
So, Sin 50° = 0.766
And g= 9.8
Now formula for the time of flight is:
T = (2⋅u⋅sinθ)/g
T = (2 × 20 × sin50°)/9.8
= (2 × 20 × 0.766)/9.8
= 30.64/9.8
T = 3.12 sec
Therefore the time of flight is 3.12 seconds.
Projectile on an Inclined Plane
The results in the case of a projectile on an inclined plane are important from the competitive point of view only.
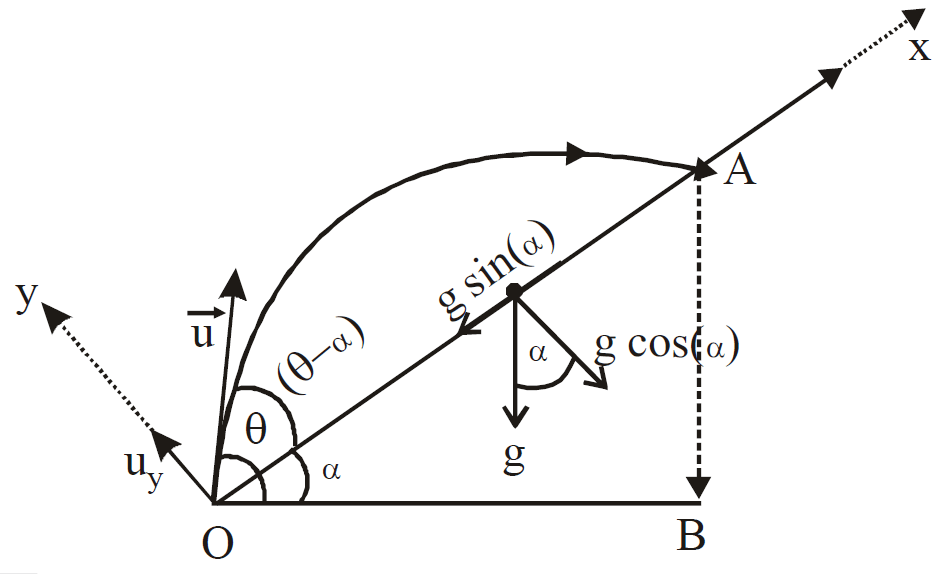
 ) along the incline, + x-axis)
) along the incline, + x-axis) ) along the incline, + y-axis)
) along the incline, + y-axis)(A) Time of Flight
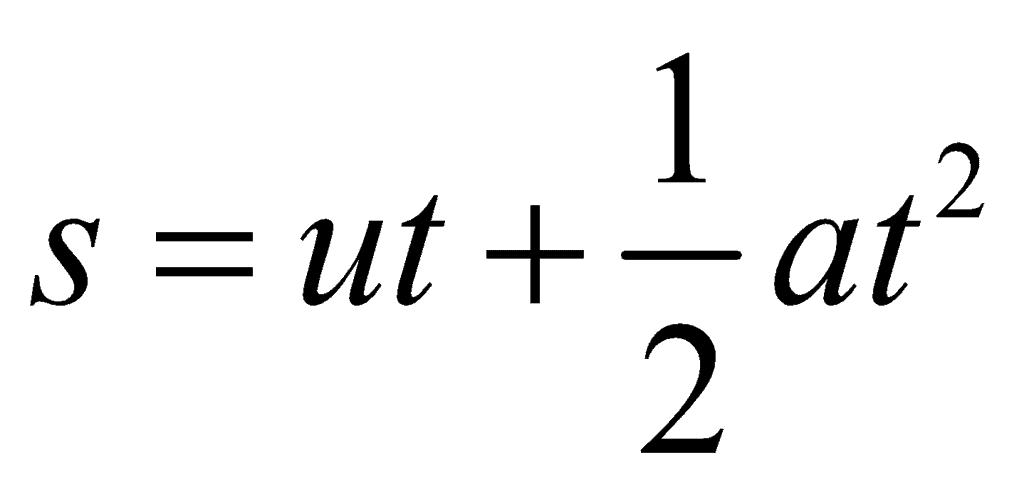
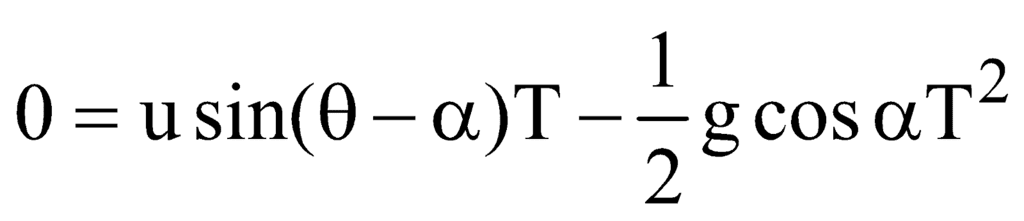
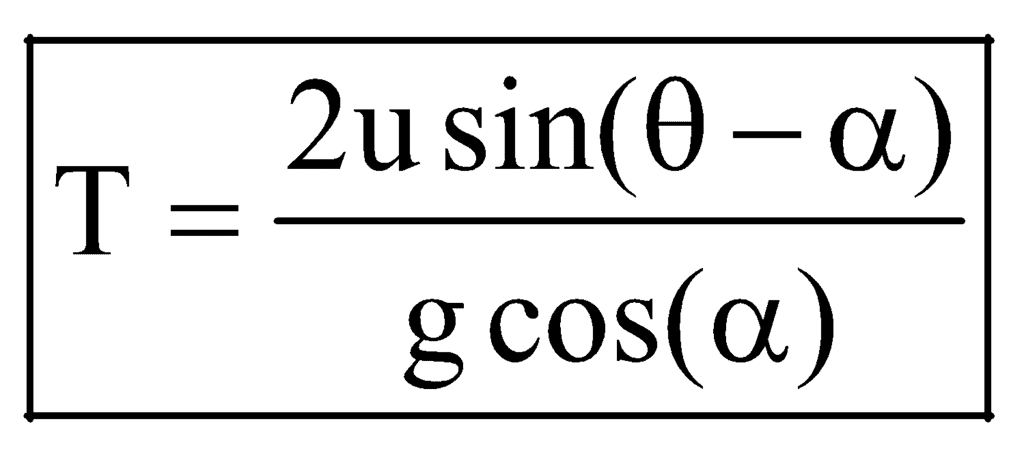
(B) Horizontal Range
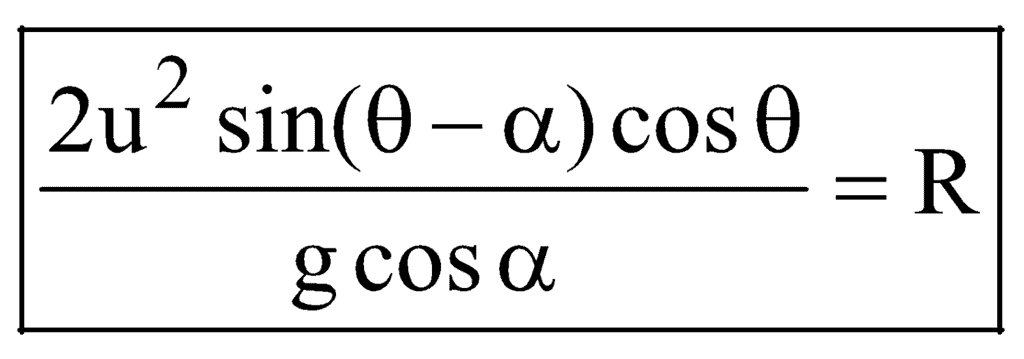
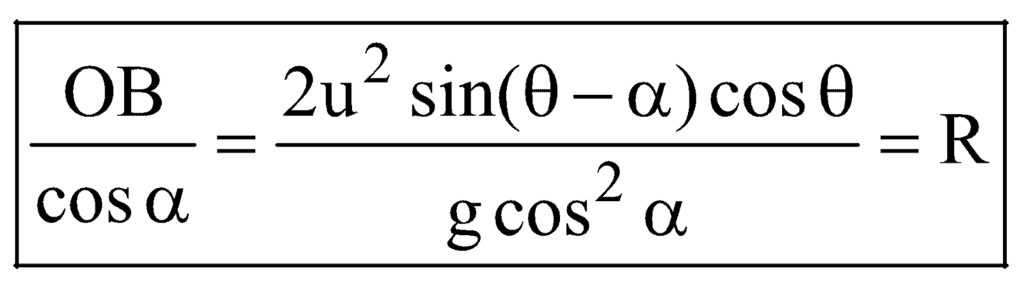
(C) Maximum Range of Projectile on Inclined Plane
Range 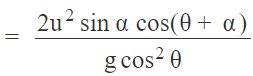 would be maximum when
would be maximum when 
(D) Maximum Distance of Projectile from the Inclined Plane
At maximum distance, H, vy = 0, so using v2y = v2y - 2g cos θH or H 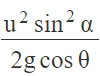
Summary
- The linear momentum at the highest point is mu cos Θ and the kinetic energy is (1/2)m(u cos Θ)2
- After t seconds, the horizontal displacement of the projectile is x = (u cos Θ) t
- After t seconds, the vertical displacement of the projectile is y = (u sin Θ) t – (1/2) gt2
- The equation of the path of the projectile is y = x tan Θ – [g/(2(u2 cos Θ)2)]x2
- The path of a projectile is parabolic.
- At the lowest point, the kinetic energy is (1/2) mu2
- At the lowest point, the linear momentum is = mu
- Throughout the motion, the acceleration of the projectile is constant and acts vertically downwards being equal to g.
- The angular momentum of projectile = mu cos Θ × h where the value of h denotes the height.
- The angle between the velocity and acceleration in the case of angular projection varies from 0 < Θ < 180 degrees.
Important Questions for Exam
Q.1. In which of the following states does a body possess kinetic energy?
a) Rest
b) Motion
c) When placed on a platform
d) In zero gravity
Answer: b
Explanation: The body moves in the state of motion. Hence it has a velocity and so kinetic energy. Kinetic energy = (1/2)mv2.
2. Which of the following types of motion can be used for describing the motion of a car on a straight road?
a) Rectilinear
b) Circular
c) Periodic
d) Harmonic
Answer: a
Explanation: The motion of a car on straight road is happening along a straight line. Hence the motion can be called rectilinear as rectilinear motion happens along a straight line. Rest all are non rectilinear motions.
3. Which of the following types of motion cannot describe the motion of a clock’s hands?
a) Rectilinear
b) Circular
c) Periodic
d) Harmonic
Answer: a
Explanation: The hands of a clock move in a circular manner. Hence, the motion exhibited is circular motion. Moreover, it happens periodically, so it is also periodic motion. But its is not rectilinear motion.
4. When a body is in the state of complete rest, what kind of energy does it possess?
a) Potential energy
b) Kinetic energy
c) Total energy
d) Heat energy
Answer: a
Explanation: When the body is in the state of rest, there is no motion. Hence there is no kinetic energy, hence the total energy of the body is stored as its potential energy. The total energy is the sum of kinetic and potential energies.
5. Which of the following are obtained by dividing total displacement by total time taken?
a) Average velocity
b) Instantaneous velocity
c) Uniform velocity
d) Speed
Answer: a
Explanation: The average velocity is obtained by dividing total displacement by total time taken. Instantaneous velocity is calculated at an instant and not over a period of time. Speed is distance divided by time. Velocity is said to be uniform when velocity at every instant is equal to the average velocity.
|
96 videos|367 docs|98 tests
|
FAQs on Projectile Motion - Physics Class 11 - NEET
| 1. What is the definition of projectile motion? |  |
| 2. What are the main assumptions made in analyzing projectile motion? |  |
| 3. What are the components of projectile motion? |  |
| 4. How does horizontal projectile motion differ from oblique projectile motion? |  |
| 5. What is the significance of complementary angles in projectile motion? |  |






















