NCERT Exemplar Solutions: Rational Numbers- 1 | Mathematics (Maths) Class 8 PDF Download
Exercise Page: 9
In question 1 to 25, there are four options out of which one is correct choose the correct answer.
Q.1. A number which can be expressed as p/q where p and q are integers and q≠0 is
(a) natural number.
(b) whole number.
(c) integer.
(d) rational number
Ans: (d) rational number
Solution: A number which can be expressed as p/q where p and q are integers and q≠0 is (d) rational number
 Rational Numbers
Rational Numbers
Q.2. A number of the form p/q is said to be a rational number if
(a) p and q are integers.
(b) p and q are integers and q ≠ 0
(c) p and q are integers and p ≠ 0
(d) p and q are integers and p ≠ 0 also q ≠ 0
Ans: p and q are integers and q ≠ 0
Solution:- A number of the form p/q is said to be a rational number if (b) p and q are integers and q ≠ 0
Q.3. The numerical expression (3/8) + (-5/7) = (-19/56) shows that
(a) rational numbers are closed under addition.
(b) rational numbers are not closed under addition.
(c) rational numbers are closed under multiplication.
(d) addition of rational numbers is not commutative.
Ans: (a) rational numbers are closed under addition.
Solution:
Because, (3/8) + (-5/7)
Take the LCM of the denominators of the given rational numbers.
LCM of 8 and 7 is 56
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(3/8)= [(3×7)/ (8×7)] = (21/56)
(-5/7)= [(-5×8)/ (7×8)] = (-40/56)
Then,
= (21/56) + (-40/56) … [∵ denominator is same in both the rational numbers]
= (21 – 40)/56
= (-19/56)
Q.5. (-3/8) + (1/7) = (1/7) + (-3/8) is an example to show that
(a) addition of rational numbers is commutative.
(b) rational numbers are closed under addition.
(c) addition of rational number is associative.
(d) rational numbers are distributive under addition.
Ans: (a) addition of rational numbers is commutative.
Solution: The arrangement of above rational numbers is in the form of Commutative law of addition [a + b=b + a]
Q.6. Which of the following expressions shows that rational numbers are associative under multiplication.
(a) [(2/3) × ((-6/7) × (3/5))] = [((2/3) × (-6/7)) × (3/5)]
(b) [(2/3) × ((-6/7) × (3/5))] = [(2/3) × ((3/5) × (6/7))]
(c) [(2/3) × ((-6/7) × (3/5))] = [((3/5) × (-2/3)) × (-6/7)]
(d) [((2/3) × (-6/7)) × (3/5)] = [((-6/7) × (2/3)) × (-3/5)]
Ans: (a) [(2/3) × ((-6/7) × (3/5))] = [((2/3) × (-6/7)) × (3/5)]
Solution: Because, the arrangement of above rational numbers is in the form of Associative law of Multiplication [a × (b ×c)] = [(a× b) × c]
Q.7. Zero (0) is
(a) the identity for addition of rational numbers.
(b) the identity for subtraction of rational numbers.
(c) the identity for multiplication of rational numbers.
(d) the identity for division of rational numbers.
Ans: (a) the identity for addition of rational numbers.
Solution: Zero (0) is (a) the identity for addition of rational numbers.
8. One (1) is
(a) the identity for addition of rational numbers.
(b) the identity for subtraction of rational numbers.
(c) the identity for multiplication of rational numbers.
(d) the identity for division of rational numbers.
Ans: (c) the identity for multiplication of rational numbers.
Solution: One (1) is the identity for multiplication of rational numbers.
Q.9. The additive inverse of -7/19 is
(a) -7/19
(b) 7/19
(c) 19/7
(d) -19/7
Ans: (b) 7/19
Solution: Additive inverse of (-7/19) is (b) (7/19)
The additive inverse of the rational number -a/b is a/b and vice-versa.
Q.10. Multiplicative inverse of a negative rational number is
(a) a positive rational number.
(b) a negative rational number.
(c) 0
(d) 1
Ans: (b) a negative rational number.
Solution:
(-1/3) is a rational number so its multiplicative inverse is (-3/1)
So that their multiplication will be,
= (-1/3) × (-3/1)
= – 1 × -1
= 1
Q.11. If x + 0 = 0 + x = x, which is rational number, then 0 is called
(a) identity for addition of rational numbers.
(b) additive inverse of x.
(c) multiplicative inverse of x.
(d) reciprocal of x.
Ans: (a) identity for addition of rational numbers.
Solution: Sum of any rational number and zero is always a rational number.
Therefore, zero is the identity for addition of rational numbers.
Q.12. To get the product 1, we should multiply (8/21) by
(a) 8/21
(b) -8/21
(c) 21/8
(d) -21/8
Ans: (c) 21/8
Solution:
Because,
= (8/21) × (21/8)
= (8 × 21) / (21 × 8)
= 168/168
= 1
Q.13. – (-x) is same as
(a) –x
(b) x
(c) 1/x
(d) -1/x
Ans: (b) x
Solution: We know that, (- × – = +)
14. The multiplicative inverse of 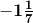 is
is
(a) 8/7
(b) -8/7
(c) 7/8
(d) 7/-8
Ans: (d) 7/-8
Solution:
=
= – 8/7
= 7/-8 [∵ reciprocal]
Q.15. If x be any rational number then x + 0 is equal to
(a) x
(b) 0
(c) –x
(d) Not defined
Ans: (a) x
Solution:
= x + 0 = x [∵ identity for addition of rational numbers]
Q.16. The reciprocal of 1 is
(a) 1
(b) -1
(c) 0
(d) Not defined
Ans: (a) 1
Solution:
Reciprocal of 1 = 1/1
= 1
Q.17. The reciprocal of -1 is
(a) 1
(b) -1
(c) 0
(d) Not defined
Ans: (b) -1
Solution: Reciprocal of -1 = -1/1
= -1
Q.18. The reciprocal of 0 is
(a) 1
(b) -1
(c) 0
(d) Not defined
Ans: (d) Not defined
Solution: Reciprocal of 0 = 1/0
= not defined
Q.19. The reciprocal of any rational number p/q, where p and q are integers and q ≠ 0, is
(a) p/q
(b) 1
(c) 0
(d) q/p
Ans: (d) q/p
Solution: The reciprocal of p/q = q/p
Q.20. If y be the reciprocal of rational number x, then the reciprocal of y will be
(a) x
(b) y
(c) x/y
(d) y/x
Ans: (a) x
Solution:
If y be the reciprocal of rational number x, i.e. y = 1/x
x = 1/y
Then,
Reciprocal of y = x
Q.21. The reciprocal of (-3/8) × (-7/13) is
(a) 104/21
(b) -104/21
(c) 21/104
(d) -21/104
Ans: (a) 104/21
Solution:
= (-3 × -7) / (8 × 13)
= (21/104)
Reciprocal of 21/104 is 104/21
Q.22. Which of the following is an example of distributive property of multiplication over addition for rational numbers.
(a) – (1/4) × {(2/3) + (-4/7)} = [-(1/4) × (2/3)] + [(-1/4) × (-4/7)]
(b) – (1/4) × {(2/3) + (-4/7)} = [(1/4) × (2/3)] – (-4/7)
(c) – (1/4) × {(2/3) + (-4/7)} = (2/3) + (-1/4) × (-4/7)
(d) – (1/4) × {(2/3) + (-4/7)} = {(2/3) + (-4/7)} – (1/4)
Ans: (a) – (1/4) × {(2/3) + (-4/7)} = [-(1/4) × (2/3)] + [(-1/4) × (-4/7)]
Solution: Because we know the rule of distributive law, i.e. a × (b + c)] = [(a × b) + (a × c)
Q.23. Between two given rational numbers, we can find
(a) one and only one rational number.
(b) only two rational numbers.
(c) only ten rational numbers.
(d) infinitely many rational numbers.
Ans: (d) infinitely many rational numbers.
Solution: Between two given rational numbers, we can find infinitely many rational numbers.
Q.24. (x + y)/2 is a rational number
(a) Between x and y
(b) Less than x and y both.
(c) Greater than x and y both.
(d) Less than x but greater than y
Ans: (a) Between x and y
Solution:
Let us assume the value of x and y is 4 and 8 respectively
Then,
= (4 + 8)/ 2
= 12/2
= 6
Hence, the value 6 is lies between 4 and 8.
Q.25. Which of the following statements is always true?
(a) (x – y)/2 is a rational number between x and y.
(b) (x + y)/2 is a rational number between x and y.
(c) (x × y)/2 is a rational number between x and y.
(d) (x ÷ y)/2 is a rational number between x and y.
Ans: (x + y)/2 is a rational number between x and y.
Solution: (b) (x + y)/2 is a rational number between x and y
Let us assume the value of x and y is 6 and 9 respectively
Then,
= (6 + 9)/ 2
= 14/2
= 7
Hence, the value 7 is lies between 6 and 9.
In questions 26 to 47, fill in the blanks to make the statements true.
Q.26. The equivalent of 5/7, whose numerator is 45 is _______.
Solution: Form the question it is given that equivalent of 5/7 = 45/denominator
To get 45 in the numerator multiply both numerator and denominator by 9
Then,
= (5 × 9)/ (7 × 9)
= 45/63
So, the equivalent of 5/7, whose numerator is 45 is (45/63)
Q.27. The equivalent rational number of 7/9, whose denominator is 45 is _______.
Solution: Form the question it is given that equivalent of 7/9 = Numerator/45
To get 45 in the denominator multiply both numerator and denominator by 5
Then,
= (7 × 5)/ (9 × 5)
= 35/45
So, the equivalent rational number of 7/9, whose denominator is 45 is (35/45)
Q.28. Between the numbers (15/20) and (35/40), the greater number is _______.
Solution: The LCM of the denominators 20 and 40 is 40
∴ (15/20) = [(15×2)/ (20×2)] = (30/40)
and (35/40) = [(35×1)/ (40×1)] = (35/40)
Now, 30 < 35
⇒ (30/40) < (35/40)
Hence, (15/20) < (35/40)
∴ 35/40 is greater.
So, between the numbers (15/20) and (35/40), the greater number is (35/40).
Q.29. The reciprocal of a positive rational number is _______.
Solution: The reciprocal of a positive rational number is positive rational number.
Let us take positive rational number 2/3
The reciprocal of this positive rational number is 3/2 (positive rational number)
Q.30. The reciprocal of a negative rational number is _______.
Solution: The reciprocal of a negative rational number is negative rational number.
Let us take negative rational number -3/4
The reciprocal of a negative rational number is 4/-3 = -4/3
Q.31. Zero has _______ reciprocal.
Solution: Zero has no reciprocal.
The reciprocal of 0 = 1/0
= Undefined
Q.32. The numbers _______ and _______ are their own reciprocal.
Solution: The numbers 1 and -1 are their own reciprocal.
Reciprocal of 1 = 1/1 = 1
Reciprocal of -1 = 1/-1 = -1
Q.33. If y be the reciprocal of x, then the reciprocal of y2 in terms of x will be _______.
Solution: If y be the reciprocal of x, then the reciprocal of y2 in terms of x will be x2.
From the question, (1/x) = y
Then,
Reciprocal of y2 = 1/x2
Substitute (1/x) in the place of y,
= 1/ (1/x)2
= x2/1
= x2
Q.34. The reciprocal of (2/5) × (-4/9) is _______.
Solution:
= (2 × -4)/ (5 × 9)
= -8/45
Reciprocal = -45/8
Hence, the reciprocal of (2/5) × (-4/5) is -45/8.
Q.35. (213 × 657)-1 = 213-1 × _______.
Solution: Let us assume the missing number be x
Then,
= 1 / (213 × 657) = (1/213) × (x)
X = 213/ (213/657)
X = 1/657
X = 657-1
So, (213 × 657)-1 = 213-1 × 657-1
Q.36. The negative of 1 is _______.
Solution: The negative of 1 is -1.
Q.37. For rational numbers (a/b), (c/d) and (e/f) we have (a/b) × ((c/d) + (e/f)) = _______ + _______
Solution: For rational numbers (a/b), (c/d) and (e/f) we have (a/b) × ((c/d) + (e/f)) = ((a/b) × (c/d)) + ((a/b) × (e/f))
Q.38. -5/7 is _______ than -3.
Solution: -5/7 is more than -3.
Q.39. There are _______ rational numbers between any two rational numbers.
Solution: There are infinitely many rational numbers between any two rational numbers.
Q.40. The rational numbers 1/3 and -1/3 are on the _______ sides of zero on the number line.
Solution: The rational numbers 1/3 and -1/3 are on the opposite sides of zero on the number line.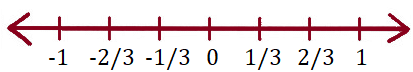
Q.41. The negative of a negative rational number is always a ________ rational number.
Solution: The negative of a negative rational number is always a positive rational number.
Example, let – a be a negative rational number.
Then, negative of a negative rational number = – (-a) = a positive rational number.
Q.42. Rational numbers can be added or multiplied in any _______.
Solution: Rational numbers can be added or multiplied in any order.
Q.43. The reciprocal of -5/7 is _______.
Solution: The reciprocal of -5/7 is -7/5.
Q.44. The multiplicative inverse of 4/3 is _______.
Solution: The multiplicative inverse of 4/3 is ¾.
Q.45. The rational number 10.11 in the from p/q is _______.
Solution: The rational number 10.11 in the from p/q is 1011/100.
Q.46. (1/5) × [(2/7) + (3/8)] = [(1/5) × (2/7)] + _______ x _______.
Solution: (1/5) × [(2/7) + (3/8)] = [(1/5) × (2/7)] + [(1/5) × (3/8)]
∵ From the rule of distributive law of multiplication [a × (b + c) = (a × b) + (a × c)]
Q.47. The two rational numbers lying between –2 and –5 with denominator as 1 are _________ and _________.
Solution: The two rational numbers lying between –2 and –5 with denominator as 1 are -3 and -4.
In each of the following, state whether the statements are true (T) or false (F).
Q.48. If x/y is a rational number, then y is always a whole number.
Solution: False.
If x/y is a rational numbers, then y is not equal to 0.
But 0 is a whole number.
Q.49. If p/q is a rational number, then p cannot be equal to zero.
Solution: False.
If p/q is a rational number, p can be equal to zero (0) or any integer.
Q.51. 5/6 lies between 2/3 and 1.
Solution: True.
Express each of the given rational numbers with 6 as the common denominator.
Now,
(2/3)= [(2×3)/ (2×2)] = (4/6)
(1)= [(1×6)/ (1×6)] = (6/6)
Then,
= 4/6 < 5/6 < 6/6
= 2/3 < 5/6 < 1
So, 5/6 lies between 2/3 and 1.
Q.52. 5/10 lies between ½ and 1.
Solution: False.
Express each of the given rational numbers with 10 as the common denominator.
Now,
½ = [(1×5)/ (2×5)] = (5/10)
(1)= [(1×10)/ (1×10)] = (10/10)
Then,
½ is equal to 5/10
So, 5/6 does not lies between ½ and 1.
Q.53. -7/2 lies between -3 and -4.
Solution: True.
Express each of the given rational numbers with 2 as the common denominator.
Now,
-3/1 = [(-3×2)/ (1×2)] = (-6/2)
-4/1 = [(-4×2)/ (1×2)] = (-8/2)
Then,
-8/2 > -7/2 > -6/2
-4 > -7/2 > -3
So, -7/2 is lies between -3 and -4.
Q.54. 9/6 lies between 1 and 2.
Solution: True.
Express each of the given rational numbers with 6 as the common denominator.
Now,
1/1 = [(1×6)/ (1×6)] = (6/6)
2/1 = [(2×6)/ (1×6)] = (12/6)
Then,
6/6 < 9/6 < 12/6
1 < 9/6 < 2
So, 9/6 is lies between 1 and 2.
Q.55. If a ≠ 0, the multiplicative inverse of a/b is b/a.
Solution: True.
Q.56. The multiplicative inverse of -3/5 is 5/3
Solution: False.
Because, the correct answer is reciprocal of a negative rational number is negative rational number. i.e. reciprocal of -3/5 is -5/3.
Q.57. The additive inverse of ½ is -2.
Solution: False.
The additive inverse of ½ is -½.
Q.58. If x/y is the additive inverse of c/d, then (x/y) + (c/d) = 0
Solution: True.
Let x/y = ½ and its additive inverse c/d = -1/2
Then, (x/y) + (c/d)
= ½ + (-½ )
= ½ – ½
= 0
Q.59. For every rational number x, x + 1 = x.
Solution: False.
Let x = 3
Then, 3 + 1 = 4
3 ≠ 4
So, it is clear that x + 1 ≠ x
Q.60. If x/y is the additive inverse of c/d, then, (x/y) – (c/d) = 0
Solution: False.
Let x/y = 2/3 and its additive inverse c/d = -2/3
Then, (x/y) – (c/d)
= (2/3) – (-2/3)
= (2/3) + (2/3)
= 4/3
Q.61. The reciprocal of a non-zero rational number q/p is the rational number q/p.
Solution: False.
Reciprocal of non-zero rational number q/p is p/q.
Q.62. If x + y = 0, then –y is known as the negative of x, where x and y are rational numbers.
Solution: False.
If x and y are rational numbers, then y is known as the negative of x
Q.63. The negative of the negative of any rational number is the number itself.
Solution: True.
Let y be a positive rational number.
Then,
The negative of the negative of y is = – (- y)
= y
Q.64. The negative of 0 does not exist.
Solution: True.
Q.65. The negative of 1 is 1 itself.
Solution: False.
The negative of 1 = -1
Q.66. For all rational numbers x and y, x – y = y – x.
Solution: False.
Let x = 2, y = 3
Then,
LHS = x – y
= 2 – 3
= -1
RHS = y – x
= 3 – 2
= 1
By comparing LHS and RHS
-1 ≠ 1
LHS ≠ RHS
Q.67. For all rational numbers x and y, (x) × (y) = (y) × (x)
Solution: True.
Let x = 2, y = 3
Then,
LHS = 2 × 3
= 6
RHS = 3 × 2
= 6
By comparing LHS and RHS
6 = 6
LHS = RHS
Q.68. For every rational number x, x × 0 = x.
Solution: False.
Let x = 2
Then,
For every rational number x
(x) × (0) = 0
2 × 0 = 0
Q.69. For every rational numbers x, y and z, x + (y × z) = (x + y) × (x + z).
Solution: False.
For every rational numbers a, b and c, [a × (b + c) = (a × b) + (a × c)]
Q.70. For all rational numbers a, b and c, a (b + c) = ab + bc.
Solution: False.
Because, for every rational numbers a, b and c, [a × (b + c) = (a × b) + (a × c)]
Q.71. 1 is the only number which is its own reciprocal.
Solution: False.
Because, the reciprocal of -1 is -1 and reciprocal of 1 is 1.
Q.72. –1 is not the reciprocal of any rational number.
Solution: False.
The reciprocal of-1 is -1.
73. For any rational number x, x + (–1) = –x.
Solution: False.
The correct form is for any rational number x, (x) × (-1) = – x.
Q.74. For rational numbers x and y, if x < y then x – y is a positive rational number.
Solution: False.
Because, for rational numbers x and y, if x < y then x – y is a negative rational number.
Example, let x = 2 and y = 3
Then,
= X – y
= 2 – 3
= -1
Q.75. If x and y are negative rational numbers, then so is x + y.
Solution: True.
For example,
Let x = – 1/3 and y = -2/3
Then,
= x + y
= (-1/3) + (-2/3)
= -1/3 – 2/3
= -3/3
= – 1
Q.76. Between any two rational numbers there are exactly ten rational numbers.
Solution: False.
Between any two rational numbers there are infinite rational numbers.
Q.77. Rational numbers are closed under addition and multiplication but not under subtraction.
Solution: False.
Rational numbers are closed under addition, subtraction and multiplication.
Q.78. Subtraction of rational number is commutative.
Solution: False.
Subtraction of rational number is not commutative.
Let x and y are any two rational number,
Then, x – y ≠ y – x
Q.80. 0 is a rational number.
Solution: True.
Because, 0/1 is a rational number.
Q.81. All positive rational numbers lie between 0 and 1000.
Solution: False.
There are infinite positive rational number on the right side of 0 on the number line.
Q.82. The population of India in 2004 – 05 is a rational number.
Solution: True.
The population of India can always be a whole number. Hence, it is also a rational number.
Q.83. There are countless rational numbers between 5/6 and 8/9.
Solution: True.
Q.84. The reciprocal of x-1 is 1/x.
Solution: False.
X-1 = 1/x
Then, reciprocal of 1/x = x/1 = x
Q.85. The rational number 57/23 lies to the left of zero on the number line.
Solution: False.
The given rational number is positive so it is lies to the right side of 0 on the number line.
Q.86. The rational number 7/-4 is lies to the right side zero on the number line.
Solution: False.
The given rational number is negative so it is lies to the left side of 0 on the number line.
Q.87. The rational number -8/-3 lies neither to the right nor to the left of zero on the number line.
Solution: False.
-8/-3 is written as 8/3 it is a positive rational number. So it is lies to the right side of 0 on the number line.
Q88. The rational numbers ½ and –1 are on the opposite sides of zero on the number line.
Solution: True.
½ is positive rational number so it is lies to the right side of 0 on the number line.
-1 is negative rational number so it is lies to the left side of 0 on the number line.
Q.89. Every fraction is a rational number.
Solution: True.
Because rational numbers can be expressed in the p/q form and fraction is also a part of whole which can be expressed in the form of p/q.
Q.90. Every integer is a rational number.
Solution: True.
In integer denominator remain 1. So, every integer is a rational number.
Q.91. The rational numbers can be represented on the number line.
Solution: True.
Q.92. The negative of a negative rational number is a positive rational number.
Solution: True.
Example, let us take -½ is a negative rational number.
Then negative of negative rational number = – (-½)
= ½ (positive rational number)
Q.93. If x and y are two rational numbers such that x > y, then x – y is always a positive rational number.
Solution:
True.
Let x = 4, y = 2
Then,
= x – y
= 4 – 2
= 2
Q.94. 0 is the smallest rational number
Solution: False.
Negative rational number below 0 is infinite. So, the smallest rational number does not exist.
Q.95. Every whole number is an integer.
Solution: True.
Every whole number is an integer but, every integer is not whole number.
Q.96. Every whole number is a rational number.
Solution: True.
Q.97. 0 is whole number but it is not a rational number.
Solution: False.
0 is whole number and also a rational number.
Q.98. The rational numbers ½ and -5/2 are on the opposite sides of 0 on the number line.
Solution:
True.
½ is positive rational number so it is lies to the right side of 0 on the number line.
-5/2 is negative rational number so it is lies to the left side of 0 on the number line.
Q.99. Rational numbers can be added (or multiplied) in any order
(-4/5) × (-6/5) = (-6/5) × (-4/5)
Solution: True.
The arrangements of given rational number is as per the commutative law under multiplication. i.e. a × b = b × c
Q.100. Solve the following: Select the rational numbers from the list which are also the integers.
9/4, 8/4, 7/4, 6/4, 9/3, 8/3, 7/3, 6/3, 5/2, 4/2, 3/1, 3/2, 1/1, 0/1, -1/1, -2/1, -3/2, -4/2, -5/2, -6/2
Solution: The rational number from the given list which also the integers are,
8/4 = 2, 9/3 = 3, 6/3 = 2, 4/2 = 2, 3/1 = 3, 1/1 = 1, 0/1 = 0, -1/1 = -1, -2/1 = -2, -4/2 = -2, -6/2 = -3
|
81 videos|423 docs|31 tests
|
FAQs on NCERT Exemplar Solutions: Rational Numbers- 1 - Mathematics (Maths) Class 8
| 1. What are rational numbers? |  |
| 2. How do you add and subtract rational numbers? |  |
| 3. Can rational numbers be negative? |  |
| 4. How do you multiply and divide rational numbers? |  |
| 5. Are all integers rational numbers? |  |