RS Aggarwal Sol:s: Real Numbers - 1 - Mathematics (Maths) Class 10 PDF Download

Q1. What do you mean by Euclid's division lemma?
Sol: For any two given positive integers a and b (with b > 0) there exist unique integers q and r such that
a = bq + r, when 0 ≤ r < b.
Here, a is called the dividend, b is divisor, q is quotient and r is the remainder.
Thus, Dividend = (Divisor × Quotient) + Remainder.
Uniqueness: For fixed a and b the numbers q and r are unique - there cannot be two different pairs of integers (q, r) satisfying the relation for the same a and b.
Example: Let a = 17 and b = 5.
17 = 5 × 3 + 2, so q = 3 and r = 2.

Q2. A number when divided by 61 gives 27 as quotient and 32 as remainder. Find the number.
Sol: By Euclid's division lemma,
Dividend = (Divisor × Quotient) + Remainder
= (61 × 27) + 32
= 1647 + 32
= 1679
Required number = 1679

Q3. By what number should 1365 be divided to get 31 as the quotient and 32 as the remainder?
Sol: Let the required divisor be d. By the division relation,
1365 = (d × 31) + 32
⇒ 1365 - 32 = 31d
⇒ 1333 = 31d
⇒ d = 1333 ÷ 31 = 43
Therefore, the divisor is 43.

Q4. Using Euclid's algorithm, find the HCF of:
(i) 405 and 2520
(ii) 504 and 1188
(iii) 960 and 1575
Sol:

(i) 

• On dividing 2520 by 405, we get
• Quotient = 6, remainder = 90
• Therefore, 2520 = 405 × 6 + 90
• Dividing 405 by 90, we get
• Quotient = 4, remainder = 45
• Therefore, 405 = 90 × 4 + 45
• Dividing 90 by 45,
• Quotient = 2, remainder = 0
• Therefore, 90 = 45 × 2
• H.C.F. of 405 and 2520 is 45

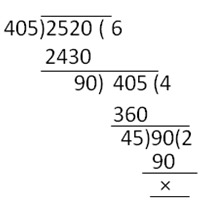
(ii) 

• Dividing 1188 by 504, we get
• Quotient = 2, remainder = 180
• Therefore, 1188 = 504 × 2 + 180
• Dividing 504 by 180,
• Quotient = 2, remainder = 144
• Therefore, 504 = 180 × 2 + 144
• Dividing 180 by 144, we get
• Quotient = 1, remainder = 36
• Dividing 144 by 36,
• Quotient = 4, remainder = 0
• Therefore, H.C.F. of 1188 and 504 is 36

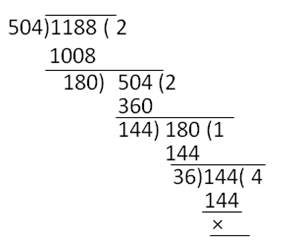
(iii) 

• Dividing 1575 by 960, we get
• Quotient = 1, remainder = 615
• 1575 = 960 × 1 + 615
• Dividing 960 by 615, we get Quotient = 1, remainder = 345
• 960 = 615 × 1 + 345
• Dividing 615 by 345, Quotient = 1, remainder = 270
• 615 = 345 × 1 + 270
• Dividing 345 by 270, we get Quotient = 1, remainder = 75
• 345 = 270 × 1 + 75
• Dividing 270 by 75, we get Quotient = 3, remainder = 45
• 270 = 75 × 3 + 45
• Dividing 75 by 45, we get Quotient = 1, remainder = 30
• 75 = 45 × 1 + 30
• Dividing 45 by 30, we get Quotient = 1, remainder = 15
• 45 = 30 × 1 + 15
• Dividing 30 by 15, we get Quotient = 2, remainder = 0
• H.C.F. of 1575 and 960 is 15

Q5. Show that every positive integer is either even or odd.
Sol: Let a be any positive integer.
On dividing a by 2, let q be the quotient and r be the remainder.
By Euclid's division lemma, a = 2q + r, where 0 ≤ r < 2
Hence r can be 0 or 1.
If r = 0, then a = 2q, so a is even.
If r = 1, then a = 2q + 1, so a is odd.
Therefore, every positive integer is either even or odd.

Q6. Show that any positive odd integer is of the form (6m + 1), (6m + 3) or (6m + 5), where m is some integer.
Sol: Let a be any positive integer.
On dividing a by 6, let m be the quotient and r be the remainder.
By Euclid's division lemma, a = 6m + r, where 0 ≤ r < 6
So r can be 0, 1, 2, 3, 4 or 5.
If r = 0, 2 or 4 then a is even (6m, 6m + 2, 6m + 4 are even).
If a is odd, r must be 1, 3 or 5.
Therefore any positive odd integer is of the form 6m + 1, 6m + 3 or 6m + 5 for some integer m.

Q7. Show that any positive odd integer is of the form (4m + 1) or (4m + 3), wherein is some integer.
Sol: Let a be a given positive odd integer.
On dividing a by 4, let m be the quotient and r be the remainder.
By Euclid's division lemma, a = 4m + r, where 0 ≤ r < 4
So r can be 0, 1, 2 or 3.
If r = 0 or r = 2 then a is even (4m or 4m + 2).
Since a is odd, r must be 1 or 3.
Thus a = 4m + 1 or a = 4m + 3 for some integer m.