Perimeter & Area of Circles | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Area of a Circle
- The area of a circle refers to the space covered by the circle in a two-dimensional plane. It is the space enclosed within the boundary or circumference of the circle. The formula to calculate the area of a circle is A = πr², where r is the radius of the circle. The unit of area is expressed in square units, such as m², cm², in², and so on.
- The area of a circle can also be calculated using the diameter (d) with the formula A = πd²/4. In these formulas, π (Pi) is a mathematical constant approximately equal to 22/7 or 3.14. Pi represents the ratio of the circumference to the diameter of any circle.
- Understanding the area of a circle is practical in various scenarios. For instance, it helps in determining the amount of cloth needed to cover a circular table or in measuring the region occupied by a circular field or plot. The area formula is also related to the circumference, which is the boundary length of the circle.
- It's important to note that a circle, being a two-dimensional shape, does not have volume. It only has area and perimeter, which is the same as its circumference. Now, let’s explore the concepts of area, surface area, and circumference of a circle in detail with examples.
Circle and Parts of a Circle
A circle is a collection of points that are at a fixed distance from the center of the circle. A circle is a closed geometric shape. We see circles in everyday life such as a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed inside the circle is known as the area of the circle.
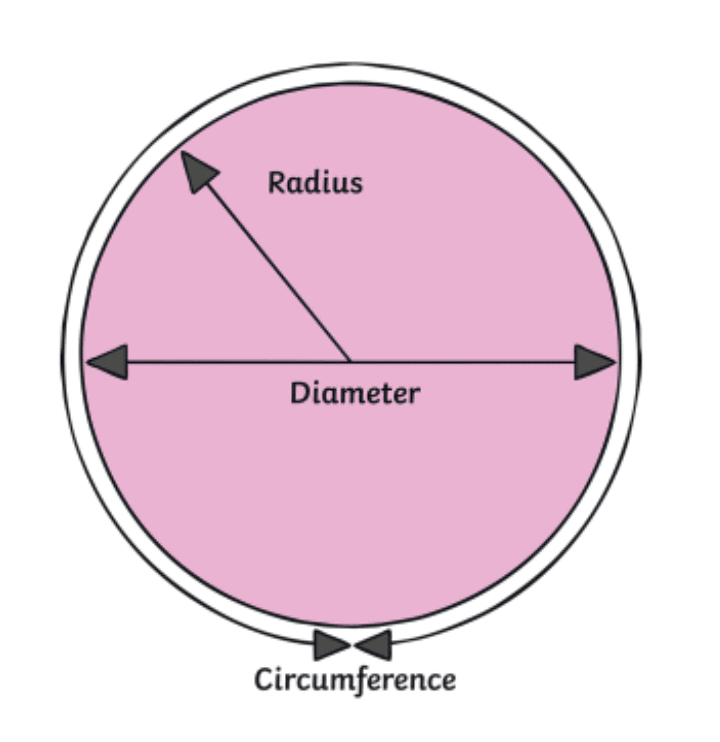
- Radius:The distance from the centre to a point on the boundary is called the radius of a circle. It is represented by the letter 'r' or 'R'. Radius plays an important role in the formula for area and circumference of a circle, which we will learn later.
- Diameter: A line that passes through the centre and its endpoints lie on the circle is called the diameter of a circle. It is represented by the letter 'd' or 'D'.
The diameter of a circle is twice its radius. Diameter = 2 × Radius
d = 2r or D = 2R
If the diameter of a circle is known, its radius can be calculated as:
r = d/2 or R = D/2 - Circumference:The circumference of the circle is equal to the length of its boundary. This means that perimeter of a circle is equal to its circumference. The length of rope that wraps around circle's boundary perfectly will be equal to its circumference. The below-given figure help you visualize the same. Circumference can be measured by using the given formula:
Circumference of a Circle = 2πR = πD
where 'r' is the radius of the circle and π is the mathematical constant whose value is approximated to 3.14 or 22/7. The circumference of a circle can be used to find the area of that circle.
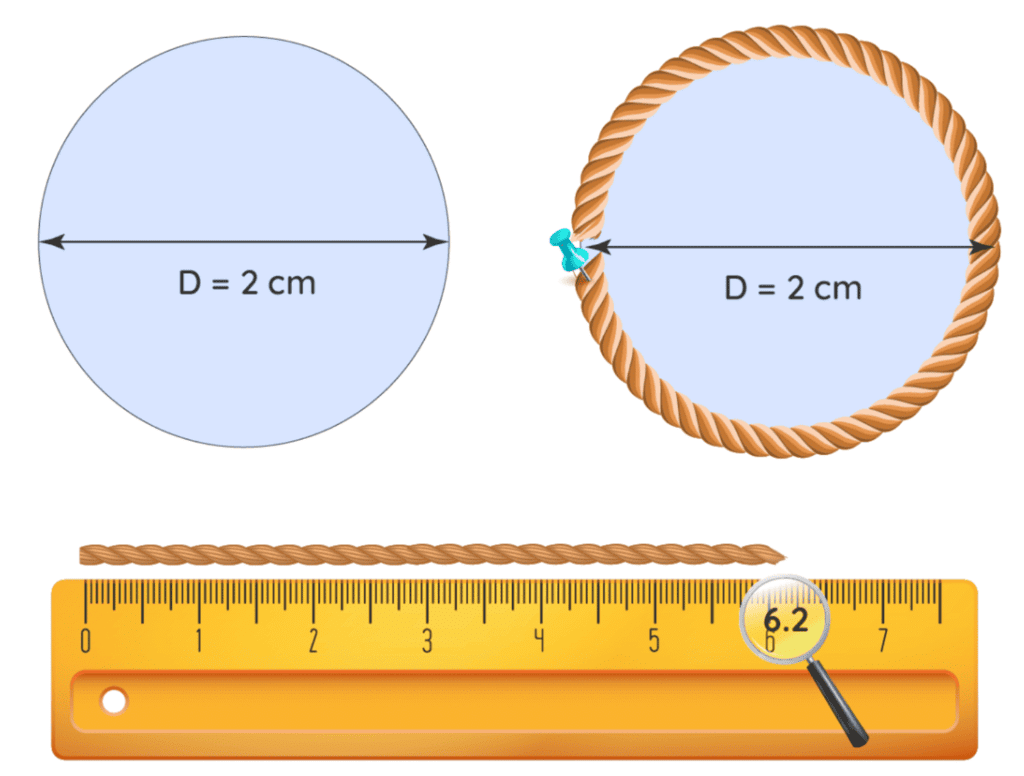 Measuring circumference with help of rope
Measuring circumference with help of rope
For a circle with radius ‘r’ and circumference ‘C’:
π = Circumference/Diameter
π = C/2r = C/d
C = 2πr
Example 1 : What is the circumference of a circle of diameter 10 cm (Take π = 3.14)?
Solution: Diameter of the circle (d) = 10 cm
Circumference of circle = πd= 3.14×10cm = 31.4cm
So, the circumference of the circle of diameter 10 cm is 31.4 cm.
Let us understand the different parts of a circle using the following real-life example.
Consider a circular-shaped park as shown in the figure below. We can identify the various parts of a circle with the help of the figure and table given below.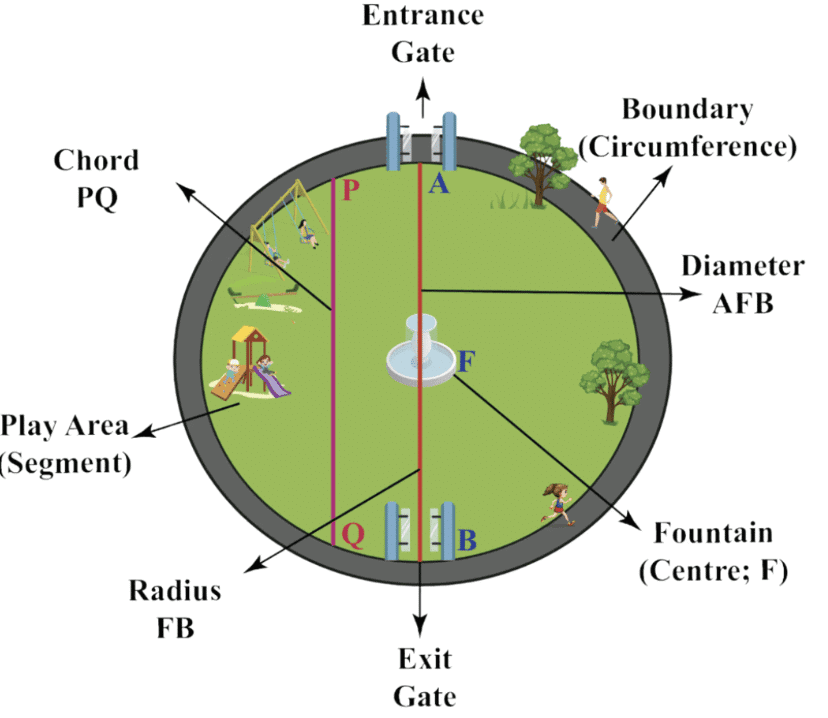
What Is the Area of Circle?
The area of a circle is the amount of space enclosed within the boundary of a circle. The region within the boundary of the circle is the area occupied by the circle. It may also be referred to as the total number of square units inside that circle. 
Area of Circle Formulas
The area of a circle can be calculated in intermediate steps from the diameter, and the circumference of a circle. From the diameter and the circumference, we can find the radius and then find the area of a circle. But these above formulae provide the shortest method to find the area of a circle. Suppose a circle has a radius 'r' then the area of circle = πr2 or πd2/4 in square units, where π = 22/7 or 3.14, and d is the diameter.
Area of a circle, A = πr2 square units
Circumference / Perimeter = 2πr units
Area of circle can be calculated by using the formulas:
- Area = π x r2, where 'r' is the radius.
- Area = (π/4) x d2, where 'd' is the diameter.
- Area = C2/4π, where 'C' is the circumference.
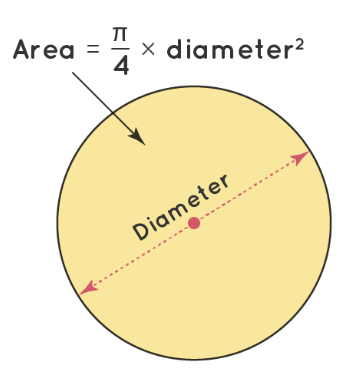
Area of a Circle Using Diameter
The Area of the circle in terms of the diameter is: Area of a Circle = πd2/4. Here 'd' is the diameter of the circle. The diameter of the circle is twice the radius of the circle. d = 2r. Generally from the diameter, we need to first find the radius of the circle and then find the area of the circle. With this formula, we can directly find the area of the circle, from the measure of the diameter of the circle.
Area of a Circle Using Circumference
The area of a circle in terms of the circumference is given by the formula. (Circumference of a Circle)2/4π. There are two simple steps to find the area of a circle from the given circumference of a circle. The circumference of a circle is first used to find the radius of the circle. This radius is further helpful to find the area of a circle. But in this formulae, we will be able to directly find the area of a circle from the circumference of the circle.
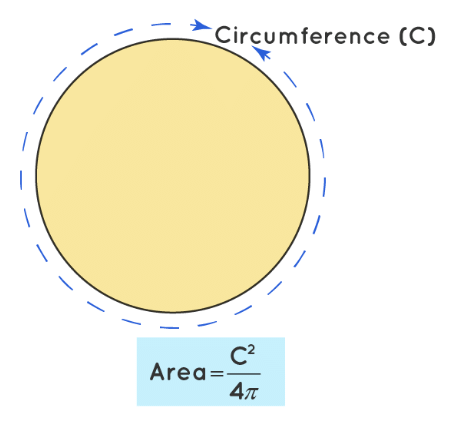
Area of a Circle-Calculation
The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle.

Derivation of Area of a Circle
Why is the area of the circle is πr2? To understand this, let's first understand how the formula for the area of a circle is derived.
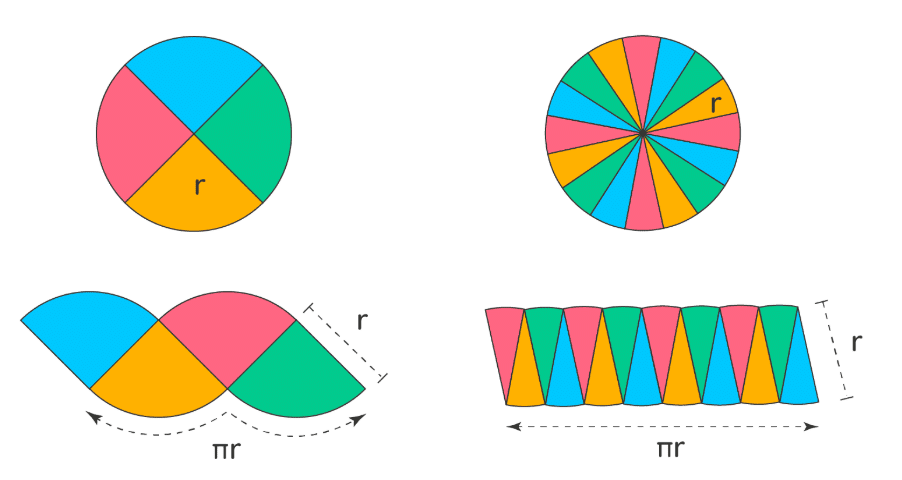
The circle can be cut into a triangle with the radius being the height of the triangle and the perimeter as its base which is 2πr. We know that the area of the triangle is found by multiplying its base by the height, and then dividing by 2, which is 1/2 x 2πr x r = πr2. Therefore, the area of the circle is πr2, where r, is the radius of the circle and the value of π is 22/7 or 3.14.
Surface area of a circle is the same as the area of a circle. In fact, when we say the area of a circle, we mean nothing but its total surface area. Surface area is the area occupied by the surface of a 3-D shape. The surface of a sphere will be spherical in shape but a circle is a simple plane 2-dimensional shape.
Example 3 :
Diameter of a circular garden is 9.8 m. Find its area.
Solution : Diameter, d=9.8m. Therefore, radius r = 9.8 ÷ 2 = 4.9m.
Area of the circle = .
|
76 videos|452 docs|39 tests
|
FAQs on Perimeter & Area of Circles - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What is the formula for calculating the area of a circle? |  |
| 2. How do you find the circumference (perimeter) of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. Can I calculate the area of a circle if I only know the circumference? |  |
| 5. Why is the value of \( \pi \) important in calculating the area and circumference of a circle? |  |
















