In questions 1 to 16, there are four options out of which one is correct. Write the correct answer.
Q.1. Both u and v vary directly with each other. When u is 10, v is 15, which of the following is not a possible pair of corresponding values of u and v?
(a) 2 and 3
(b) 8 and 12
(c) 15 and 20
(d) 25 and 37.5
Ans: c
Solution: u and v vary directly, hence,
u/v = k (constant)
Hence, u/v = 10/15 = 2/3
Now if we observe the options given,
Option (a) – 2/3
Option (b) – 8/12 = 2/3
Option (c) – 15/20 = ¾
Option (d) – 25/37.5 = 2/3
Therefore, option (c) is not the possible pair of corresponding values of u and v
Q.2. Both x and y vary inversely with each other. When x is 10, y is 6, which of the following is not a possible pair of corresponding values of x and y?
(a) 12 and 5
(b) 15 and 4
(c) 25 and 2.4
(d) 45 and 1.3
Ans: d
Solution: Since x and y vary inversely, so
xy = k (constant)
Putting the value of x and y, we get;
10×6 = 60
Now if we observe the options available;
Option (a) – 12 and 5 – 12×5 = 60
Option (b) – 15 and 4 – 15×4 = 60
Option (c) – 25 and 2.4 – 25×2.4 = 60
Option (d) – 45 and 1.3 = 45×1.3 = 58.3
Therefore, option (d) is not a possible pair of corresponding values of x and y
Q.3. Assuming land to be uniformly fertile, the area of land and the yield on it vary
(a) directly with each other.
(b) inversely with each other.
(c) neither directly nor inversely with each other.
(d) sometimes directly and sometimes inversely with each other.
Ans: a
Q.4. The number of teeth and the age of a person vary
(a) directly with each other.
(b) inversely with each other.
(c) neither directly nor inversely with each other.
(d) sometimes directly and sometimes inversely with each other
Ans: d
Q.5. A truck needs 54 litres of diesel for covering a distance of 297 km. The diesel required by the truck to cover a distance of 550 km is
(a) 100 litres
(b) 50 litres
(c) 25.16 litres
(d) 25 litres
Ans: a
Solution: Distance covered by truck using 54 litres diesel = 297 km
Distance covered by truck using 1 litre diesel = 297/54 = 5.5 km
Hence, for 550 km, diesel required = 550/5.5 = 100 litres
Q.6. By travelling at a speed of 48 kilometres per hour, a car can finish a certain journey in 10 hours. To cover the same distance in 8 hours, the speed of the car should be
(a) 60 km/h
(b) 80 km/h
(c) 30 km/h
(d) 40 km/h
Ans: a
Solution: Speed of car = 48 km/hr
Time taken = 10 hr
As we know,
Distance = speed × time = 48 × 10 = 480 km
Speed required by car to cover 480 km in 8 hours = 480/8 = 60 km/hr.
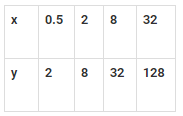
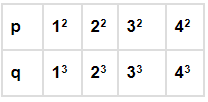
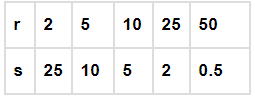
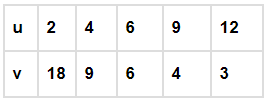
Q.7. In which of the following case, do the quantities vary directly with each other?
(a) 
(b) 
(c) 
(d) 
Ans: a
Solution: In option (a), the values of x is directly proportional to values of y, such as;
y = 4x
If we put the values of x = 0.5, 2, 8 and 32, we get the values of y as 2, 8, 32 and 128 respectively.
Q.8. Which quantities in the previous question vary inversely with each other?
(a) x and y
(b) p and q
(c) r and s
(d) u and v
Ans: d
Solution: In option (d), we can see when the value of u is increasing, the value of v is decreasing. Hence, u and v are inversely proportional.
Q.9. Which of the following vary inversely with each other?
(a) speed and distance covered.
(b) distance covered and taxi fare.
(c) distance travelled and time taken.
(d) speed and time taken.
Ans: d
Solution: By the formula of speed we know;
Speed = distance/time
As we can see here, when the time decreases, the speed increases. Hence, they inversely proportional.
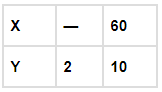
Q.10. Both x and y are in direct proportion, then 1/x and 1/y are:
(a) in indirect proportion.
(b) in inverse proportion.
(c) neither in direct nor in inverse proportion.
(d) sometimes in direct and sometimes in inverse proportion.
Ans: b
Q.11. Meenakshee cycles to her school at an average speed of 12 km/h and takes 20 minutes to reach her school. If she wants to reach her school in 12 minutes, her average speed should be
(a) 20/3 km/h
(b) 16 km/h
(c) 20 km/h
(d) 15 km/h
Ans: c
Solution: Speed = 12km/h
Time taken = 20 minutes = 20/60 hr = 1/3 hr
Distance covered = S × T = 12 × 1/3 = 4km
Speed required to cover 4km in 12 minutes = (4/12)×60 = 20 km/hr
Q.12. 100 persons had food provision for 24 days. If 20 persons left the place, the provision will last for
(a) 30 days
(b) 96/5 days
(c) 120 days
(d) 40 days
Ans: a
Solution: 100 persons have food provision for = 24 days
1 person will have food provision for = 24×100 = 2500 days
If 20 persons left the place, then total left = 100-20 = 80 persons
Hence, 80 persons have food provision for = 2400/80 = 30 days
Q.13. If two quantities x and y vary directly with each other, then
(a) x/y remains constant.
(b) x – y remains constant.
(c) x + y remains constant.
(d) x × y remains constant.
Ans: a
Solution: If x and y vary directly, then x/y = k
Q.14. If two quantities p and q vary inversely with each other, then:
(a) p/q remains constant.
(b) p + q remains constant.
(c) p × q remains constant.
(d) p – q remains constant.
Ans: c
Solution: If p and q vary inversely, then p×q = k (constant)
Q.15. If the distance travelled by a rickshaw in one hour is 10 km, then the distance travelled by the same rickshaw with the same speed in one minute is:
(a) 250/9 m
(b) 500/9 m
(c) 1000 m
(d) 500/3 m
Ans: d
Solution: Distance travelled = 10km
Time taken = 1 hr
In one minute, distance covered = 10/60 km = (10×1000)/60 m
= 500/3 m
Q.16. Both x and y vary directly with each other and when x is 10, y is 14, which of the following is not a possible pair of corresponding values of x and y?
(a) 25 and 35
(b) 35 and 25
(c) 35 and 49
(d) 15 and 21
Ans: b
Solution: x and y are directly proportional.
x ∝ y
If x = 10 and y = 14, then;
10 ∝ 14 or 5 ∝ 7
Now, if we compare,
(a) 25 ∝ 35 = 5∝7
(b) 35 ∝ 25 = 7 ∝ 5
(c) 35 ∝ 49 = 5 ∝ 7
(d) 15 ∝ 21 = 5 ∝ 7
Therefore, option (b) is not a possible pair of corresponding values of x and y.
In questions 17 to 42, fill in the blanks to make the statements true:
Q.17. If x = 5y, then x and y vary directly with each other.
Q.18. If xy = 10, then x and y vary inversely with each other.
Q.19. When two quantities x and y are in direct proportion or vary directly they are written as x ∝ y.
Q.20. When two quantities x and y are in inverse proportion or vary inversely they are written as x ∝ 1/y.
Q.21. Both x and y are said to vary inversely with each other if for some positive number k, xy = k.
Q.22. x and y are said to vary directly with each other if for some positive number k, x/y =k.
Q.23. Two quantities are said to vary directly with each other if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant.
Q.24. Two quantities are said to vary inversely with each other if an increase in one causes a decrease in the other in such a manner that the product of their corresponding values remains constant.
Q.25. If 12 pumps can empty a reservoir in 20 hours, then time required by 45 such pumps to empty the same reservoir is ______ hours.
Ans: Time taken by 12 pumps to empty a reservoir = 20 hr
Time taken by 1 pump to empty the reservoir = 20 × 12 = 240 hr
Hence, time taken by 45 pumps to empty the reservoir = 240/45 = (240×60)/45
= 14400/45 = 320 min
= 5×69 + 20 min
= 5 hour 20 min
Q.26. If x varies inversely as y, then

Ans: If x varies inversely as y, then;
x×y = k
If x = 60 and y = 10
Then, x×y = 60×10 = 600 = k
Hence, x×2 = 600
x = 600/2 = 300
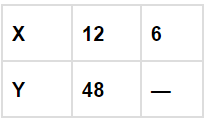
Q.27. If x varies directly as y, then

Ans: If x and y varies directly, then;
x/y = k
If x=12 and y = 48, then
k = 12/48 = ¼
Now, if x=6, and k = 1/4, then y will be;
6/y = ¼
y = 6×4=24
Q.28. When the speed remains constant, the distance travelled is directly proportional to the time.
Q.29. On increasing a, b increases in such a manner that a/b remains constant and positive, then a and b are said to vary directly with each other
Q.30. If on increasing a, b decreases in such a manner that ab remains constant and positive, then a and b are said to vary inversely with each other.
Q.31. If two quantities x and y vary directly with each other, then ratio of their corresponding values remains constant.
Q.32. If two quantities p and q vary inversely with each other then product of their corresponding values remains constant.
Q.33. The perimeter of a circle and its diameter vary directly with each other.
Q.34. A car is travelling 48 km in one hour. The distance travelled by the car in 12 minutes is _________.
Ans: Distance travelled by car in one hour = 48km
Distance travelled in one minute = 48/60 km
Distance travelled in 12 minute = (48/60)×12 = 48/5 = 9.6km
Q.35. An auto rickshaw takes 3 hours to cover a distance of 36 km. If its speed is increased by 4 km/h, the time taken by it to cover the same distance is _______.
Ans: Distance covered by auto rickshaw in 3 hours = 36km
Speed = 36/3 = 12 km/hr
If we increase the speed by 4km/hr, then the total speed becomes = 12+4 = 16km/hr
Now, the time taken by auto rickshaw will be = 36/16 = (36×60)/16 = 135 min
= 120 + 15
= 2 hour 15min
Q.36. If the thickness of a pile of 12 cardboard sheets is 45 mm, then the thickness of a pile of 240 sheets is _______ cm.
Ans: Thickness of pile of 12 cardboard sheets = 45mm
Thickness of 1 cardboard sheet = 45/12 mm
Hence, thickness of a pile of 240 sheets = (45/12)×240
= 45 × 20 = 900mm
= 900/10 cm = 90cm
Q.37. If x varies inversely as y and x = 4 when y = 6, then when x = 3 the value of y is _______.
Ans: If x varies inversely as y, then
x×y = k
4×6 = k
k=24
Now, if x = 3, then y is;
y = k/x = 24/3 = 8
Q.38. In direct proportion, a1/b1 = a2/b2
a1/b1 = a2/b2 = k
Q.39. In case of inverse proportion, a2/a1= b2/b1
Q.40. If the area occupied by 15 postal stamps is 60 cm2, then the area occupied by 120 such postal stamps will be _______.
Ans: Area occupied by 15 postal stamps = 60cm2
Area occupied by 1 postal stamps = 60/15 = 4 cm2
Area occupied by 120 such postal stamps = 4×120 = 480 cm2
Q.41. If 45 persons can complete a work in 20 days, then the time taken by 75 persons will be ______ hours.
Ans: 45 persons complete a work in 20 days
1 person can complete work in = 45 × 20 = 900 days
Time taken by 75 persons = 900/75 = 12 days = 12×24 = 288 hr
Q.42. Devangi travels 50 m distance in 75 steps, then the distance travelled in 375 steps is _______ km.
Ans: Distance travelled in 75 steps = 50m
Distance covered in 1 step = 50/75m
Distance covered in 375 steps = (50/75)×375 = 18750/75
= 250m
=250/1000 km
= 0.25km
In questions from 43 to 59, state whether the statements are true (T) or false (F).
Q.43. Two quantities x and y are said to vary directly with each other if for some rational number k, xy = k.
Ans: False
Q.44. When the speed is kept fixed, time and distance vary inversely with each other.
Ans: False
Q.45. When the distance is kept fixed, speed and time vary directly with each other.
Ans: False
Q.46. Length of a side of a square and its area vary directly with each other.
Ans: False
Q.47. Length of a side of an equilateral triangle and its perimeter vary inversely with each other.
Ans: False
Q.48. If d varies directly as t2, then we can write dt2 = k, where k is some constant.
Ans: False
Q.49. If a tree 24 m high casts a shadow of 15 m, then the height of a pole that casts a shadow of 6 m under similar conditions is 9.6 m.
Ans: True
Height of tree = 24m
Length of shadow of tree = 15m
Let height of pole = x
Length of shadow of pole = 6m
Now,
24/15 = x/6
x = (24×6)/15
x = 9.6m
Q.50. If x and y are in direct proportion, then (x – 1) and (y – 1) are also in direct proportion.
Ans: False
x and y are in direct proportion, then;
x/y = k
if x = 3 and y = 5, then
k = 3/5
Now, x-1 = 2 and y-1 = 4
(x-1)/(y-1) = 2/4 = 1/2