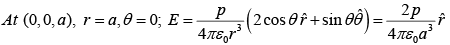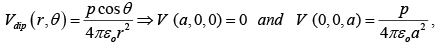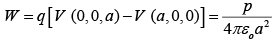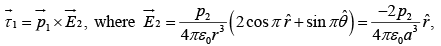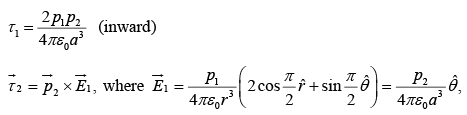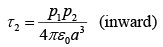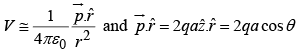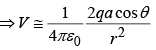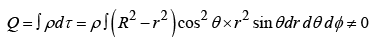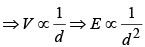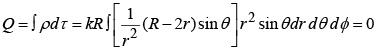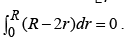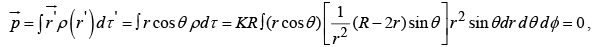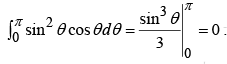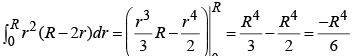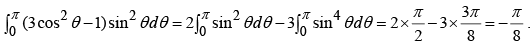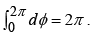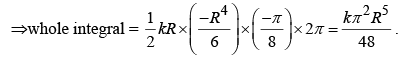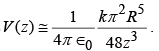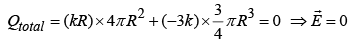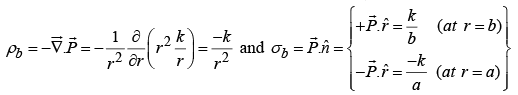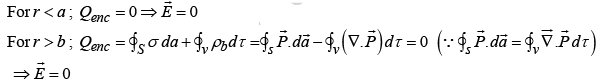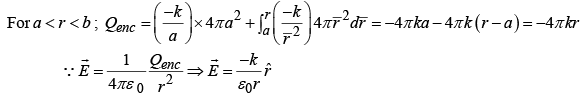Electric Dipole, Multipole Expansions & Polarisation | Electricity & Magnetism - Physics PDF Download
| Table of contents |

|
| Electric Dipole |

|
| Electric Potential and Field of a Dipole |

|
| Approximate potential at large distances |

|
| The Monopole and Dipole Terms |

|
| Polarization |

|
Electric Dipole
An electric dipole is composed of two charges, each with a magnitude of ±q, separated by a distance d. Its dipole moment is given by p = qd, with the direction extending from the -q to the +q charge.
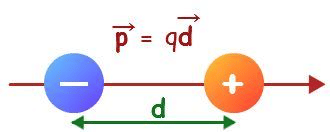 Electric Dipole
Electric Dipole
Electric Potential and Field of a Dipole
If we choose coordinates so that 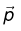 (dipole moment) lies at the origin and points in the z direction, then the potential at (r,θ ) is:
(dipole moment) lies at the origin and points in the z direction, then the potential at (r,θ ) is: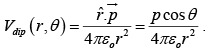
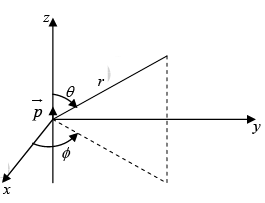
Since,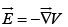
 The electric field of a dipole:
The electric field of a dipole:
We can express
Note:
(a) A dipole is placed in a uniform electric field  experiences a net force on the dipole that is zero but it experiences a torque
experiences a net force on the dipole that is zero but it experiences a torque 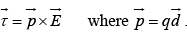
(b) In a non-uniform field, dipoles have a net force, 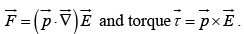
(c) Energy of an ideal dipole 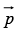 in an electric field
in an electric field 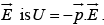 (d) Interaction energy of two dipoles separated by a distance
(d) Interaction energy of two dipoles separated by a distance 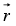 is
is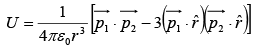
Example 1: A “pure” dipole 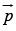 is situated at the origin, pointing in the z-direction(a) What is the force on a point charge q at ( a,0,0 ) ?(b) What is the force on q at ( 0, 0, a)?
is situated at the origin, pointing in the z-direction(a) What is the force on a point charge q at ( a,0,0 ) ?(b) What is the force on q at ( 0, 0, a)?
(c) How much work does it take to move q from ( a,0,0 ) to ( 0, 0, a )?
(a)
(b)
(c)
Example 2: In figure 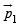 and
and 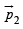 are (perfect) dipoles a distance r apart. What is the torque on
are (perfect) dipoles a distance r apart. What is the torque on 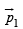 due to
due to 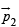 ? What is the torque on
? What is the torque on 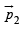 due to
due to  ?
?

Approximate potential at large distances
Approximate potential at large distances due to arbitrary localized charge distribution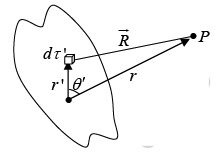
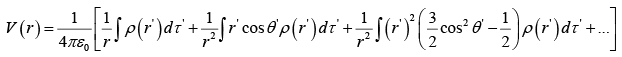
The first term ( n = 0) is the monopole contribution (it goes like 1/r). The second term ( n = 1) is the dipole term (it goes like 1/r2. The third term is quadrupole; the fourth is octopole and so on.
The lowest nonzero term in the expansion provides the approximate potential at large r and the successive terms tell us how to improve the approximation if greater precision is required.
The Monopole and Dipole Terms
Ordinarily, the multipole expansion is dominated (at large r) by the monopole term: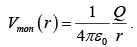
where 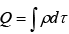 is the total charge of the configuration? If the total charge is zero, the dominant term in the potential will be the dipole (unless, of course, it also vanishes):
is the total charge of the configuration? If the total charge is zero, the dominant term in the potential will be the dipole (unless, of course, it also vanishes):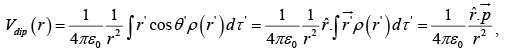
where dipole moment 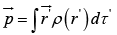 The dipole moment is determined by the geometry (size, shape, and density) of the charge distribution. The dipole moment of a collection of point charges is
The dipole moment is determined by the geometry (size, shape, and density) of the charge distribution. The dipole moment of a collection of point charges is
Note: Ordinarily, the dipole moment does change when we shift the origin, but there is an important exception: If the total charge is zero, then the dipole moment is independent of the choice of origin.
Example 3: Find the approximate potential for points on the z–axis, far from the sphere. Four particles of charges q , 3q , −2q and −2q are placed as shown in the figure, each a distance a from the origin. Find a simple approximate formula for the potential, valid at points far from the origin.
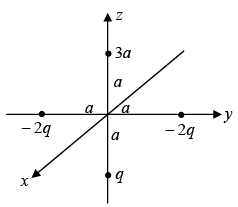
Net dipole moment
Therefore
Example 4: An insulating sphere of radius R carries a charge density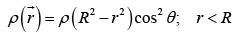 Find the leading order term for the electric field at a distance d , far away from the charge distribution.
Find the leading order term for the electric field at a distance d , far away from the charge distribution.
Example 5: A sphere of radius R, centered at the origin, carries charge density  where k is a constant, and r , θ are the usual spherical coordinates.
where k is a constant, and r , θ are the usual spherical coordinates.
Monopole term:
Since the r integral is
Dipole term:
Since the integral is
Quadrupole term: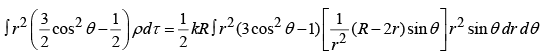
r integral :θ integral:
φ integral:
For point P on the z –axis ( r →z) the approximate potential is
Polarization
When a dielectric material is placed in an external field, neutral atoms in the substance will develop a small induced dipole moment aligned with the field. If the material consists of polar molecules, each permanent dipole will experience a torque that aligns it along the field direction. However, random thermal motions interfere with this alignment process, so complete alignment is never achieved, especially at higher temperatures, and the alignment disappears almost immediately when the field is removed.
(Polarization) ≡ dipole moment per unit volume.
The Field of a Polarized Object (Bound Charges)
Suppose we have a piece of polarized material with a polarization vector  containing a lot of microscopic dipoles lined up.
containing a lot of microscopic dipoles lined up.
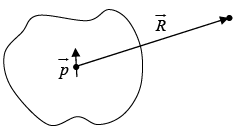
For a single dipole of dipole moment 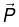 we have
we have  where
where  is the vector from the dipole to the point at which we are evaluating the potential.
is the vector from the dipole to the point at which we are evaluating the potential.
Thus,
By solving the above equation, we get
The first term looks like the potential of a surface-bound charge  (where
(where
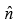 is the normal unit vector)
is the normal unit vector)
The second term looks like the potential for a volume-bound charge 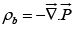
Thus the potential (and hence also the field) of a polarized object is the same as that produced by a volume charge density 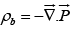 plus a surface charge density
plus a surface charge density
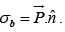
Example 6: A sphere of radius R carries a polarization 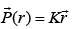 where K is a constant and
where K is a constant and 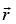 is the vector from the center.
is the vector from the center.
(a) Calculate the bound charges σb and ρb.
(b) Find the field inside and outside the sphere.
(a)
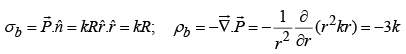
(b) For r <R ;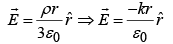
For r >R ; same as if all charge at center; but
Example 7: Consider a sphere of radius R with a polarization P=Kr2, where K is a constant and r is the vector from the center of the sphere. (a) Calculate the bound surface charge density (σb) and volume charge density (ρb). (b) Determine the electric field both inside and outside the sphere.
Solution:
(a) Bound charge densities:
The bound surface charge density σb is given by:
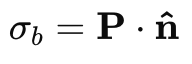
where n^ is the unit normal vector to the surface. Since P=Kr2 and r points outward from the center, we have n^=r^. Therefore,
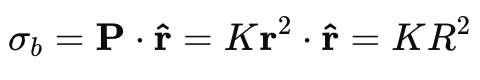
The bound volume charge density ρb is given by:
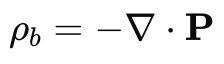
Since P=Kr2, the divergence of P is:
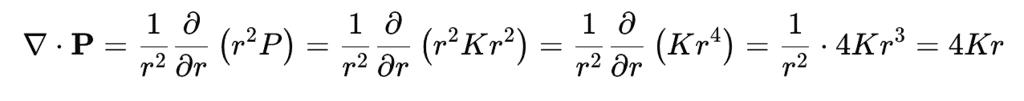 So, inside the sphere, the electric field is
So, inside the sphere, the electric field is  in the radial direction.
in the radial direction.
Outside the sphere (r>R), the electric field is the same as if the sphere were uniformly charged, which is:
where Q is the total charge enclosed by the sphere. Since the polarization is P=Kr2, the total charge Q is given by the volume integral of ∇⋅P over the sphere, which equals the volume integral of 4Kr over the sphere, and this equals 4KR3. Therefore, 
 where k is a constant and r is the distance from the center. Find the electric field in all three regions.
where k is a constant and r is the distance from the center. Find the electric field in all three regions. 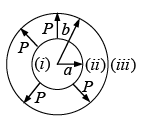
Solution:
|
82 videos|32 docs|22 tests
|
FAQs on Electric Dipole, Multipole Expansions & Polarisation - Electricity & Magnetism - Physics
| 1. How are multipole expansions used in physics and engineering? |  |
| 2. What are the different types of multipole expansions? |  |
| 3. How do you calculate the coefficients in a multipole expansion? |  |
| 4. What is the physical significance of the multipole moments in a multipole expansion? |  |
| 5. How accurate are multipole expansions in approximating complex fields or functions? |  |