Free Electron Theory of Metals | Solid State Physics, Devices & Electronics PDF Download
Free Electron Theory of Metals
The classical, Einstein, and Debye theories of specific heats of solids apply with equal degrees of success to both metals and nonmetals, which is strange because they ignore the presence of free electrons in metals.
In a typical metal each atom contributes one electron to the common “electron gas,” so in 1 kilomole of the metal there are N0 free electrons. If these electrons behave like the molecules of an ideal gas, each would have 3/2 kBT of kinetic energy on the average. The metal would then have
of internal energy per kilomole due to the electrons. The molar specific heat due to the electrons should therefore be 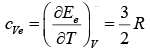
and the total specific heat of the metal should be 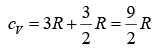
at high temperature where a classical analysis is valid. Actually, of course, the Dulong-Petit value of 3R holds at high temperatures, from which we conclude that the free electrons do not in fact contribute to the specific heat.
Electrons are fermions and obey Fermi-Dirac statistics with average energies  per degree of freedom at “high” temperature, how high is high enough for classical behaviour is not necessarily the same for the two kinds of systems in a metal.
per degree of freedom at “high” temperature, how high is high enough for classical behaviour is not necessarily the same for the two kinds of systems in a metal.
The distribution function that gives the average occupancy of a state of energy ∈ in a system of fermions is  (i)
(i)
where 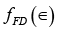 is average occupancy per state.
is average occupancy per state.
What we also need is an expression for g (∈)d ∈ , the number of quantum states available to electrons with energies between ∈ and ∈ + d∈ .
The number of standing waves in a cubical cavity L on a side is
g(f)dj = πj2dj (ii)
where j = 2 L / λ and λ is its de Broglie wavelength of λ = h/p. Electrons in a metal have nonrelativistic velocities. 
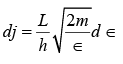
Using these expressions for j and dj in equation (ii) gives 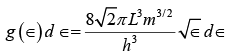
As in the case of standing waves in a cavity the exact shape of the metal sample does not matter, so we can substitute its volume V for L3 to give 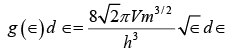 (iii)
(iii)
where g (∈)d∈ is the number of energy states in energy range ∈ and ∈ + d∈ .
Fermi Energy
We can find Fermi energy ∈F by filling up the energy states in the metal sample at T = 0 with the N free electrons it contains in order of increasing energy starting from∈= 0 . The highest state to be filled will then have the energy ∈=∈F by definition. The number of electrons that can have the same energy ∈ is equal to the number of state that have this energy, since each state is limited to one electron. Hence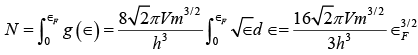
and so 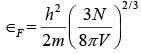 (iv)
(iv)
The number of electrons in an electron gas that have energies between ∈ and ∈+ d ∈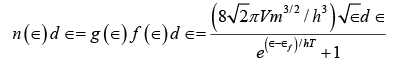 (v)
(v)
If we express the numerator of equation (v) in terms of the Fermi energy ∈F we get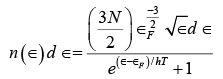 (vi)
(vi)
It is interesting to determine the average electron energy at 0 K . To do this, we first find the total energy E0 at 0 K , which is  since at T = 0K all the electrons have energies less than or equal to the Fermi energy ∈F ,
since at T = 0K all the electrons have energies less than or equal to the Fermi energy ∈F , ∵ e(∈−∈F ) / kT =e−∞= 0
∵ e(∈−∈F ) / kT =e−∞= 0
The average electron energy 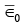 is this total energy divided by the number N of electrons present, which gives
is this total energy divided by the number N of electrons present, which gives 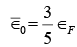 (vii)
(vii)
Since Fermi energies for metals are usually several electron volts, the average electron energy in them at 0K will also be of this order of magnitude. The temperature of an ideal gas whose molecules have an average kinetic energy of 1 eV is11, 600 K . If free electrons behaved classically, a sample of copper would have to be at a temperature of about 50,000K for its electrons to have the same average energy they actually have at 0 K.
The failure of the free electrons in a metal to contribute appreciably to its specific heat follows directly from their energy distribution-those within about kT of the Fermi energy-are because the states above them are already filled. It is unlikely that an electron with, say, an energy ∈ that is 0.5eV below ∈F can leapfrog the filled states above it to the nearest vacant state when kT at room temperature is 0.025 eV and even at 500 K is only 0.043 eV.
The specific heat of the electron gas in a metal is given by 
The coefficient of R is very much smaller than the classical figure of 3/2. The dominance of the atomic specific heat cV in a metal over the electronic specific heat is pronounced over a wide temperature range. However, at very low temperature cVe becomes significant because cV is then approximately proportional to T3 whereas cVe is proportional to T . At very high temperature cV has leveled out at about 3R while cVe has continued to increase, and the contribution of cVe to the total specific heat is then detectable.
Example 1: Find the Fermi energy in copper on the assumption that each copper atom contributes one free electron to the electron gas. (This is a reasonable assumption sice, a copper atom has a single 4s electron outside closed inner shells). The density of copper is 8.94 ×103 kg / m3 and its atomic mass is 63.5 u.
The electron density N/V in copper is equal to the number of copper atoms per unit volume. Since1u =1.66×10−27kg ,

= 8.48×1028 atoms/m3 = 8.48×1028 electrons/m3
The corresponding Fermi energy is,
= 1.13×10−18 J = 7.04eV
Density of States
The density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied.
➤ Density of states in 1-Dimension
Consider a particle of mass m confined to a line of length L . The energy levels are labeled according to the quantum number n which gives the number of half wavelength in the wavefunction.
For nth mole the wavelength is λn = 2L/n.
This can be expressed in term of wave vector K = 2π/λ
∴ Kn = nπ/L n = 1,2,3, ...
The number of K - states in interval K and K +dK is 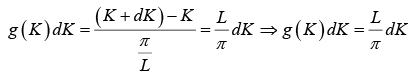
The density of state is 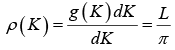
➤ Second Method
The wave function of trapped in one dimensional unbounded medium of periodic boundary condition with period ψ(x) = Aeikx
Since wave function is periodic ∴ ψ ( x ) =ψ (x+L)
⇒ Aeikx = Aeik(x + L) ⇒ eikL = 1
⇒ eikL =ei2nπ where n = 0,±1, ±2, ±3....
∴ 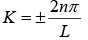 where n = 0,1, 2, 3....
where n = 0,1, 2, 3....
The number of K -states in range K and K +dK is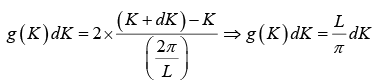
The density of state is 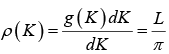
➤ Density of States in 2-Dimension
The wave function of particle trapped in two dimensional unbounded medium of periodic boundary conditions with period of L in both x and y dimensions is 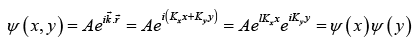
where 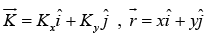 and ψ (x) = A1eikx and ψ (y) = A2eik y.
and ψ (x) = A1eikx and ψ (y) = A2eik y.
Since wave function is periodic in x & y direction
∴ ψ (x) =ψ (x+L) and ψ (y) =ψ (y + L)
This gives 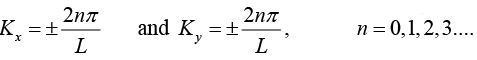
The possible values of K - states in 2 -dimensional K -space can be represented as The number of K -states in range K and K + dK 
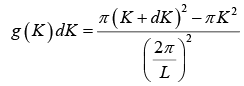
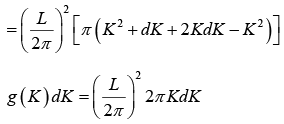
The density of state is 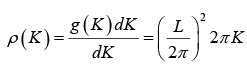
➤ Density of States in 3-Dimension
The wavefunction of particle trapped in 3 -dimensional unbounded medium of periodic boundary conditions with period L is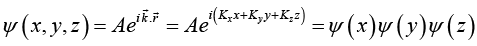
where 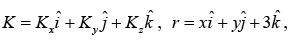 ψ (x) = A1eikx , ψ ( y) = A2eiky and ψ( z) =A3 eikz
ψ (x) = A1eikx , ψ ( y) = A2eiky and ψ( z) =A3 eikz
For periodicity
ψ (x) =ψ (x+L), ψ (y) =ψ (y + L)&ψ (z) =ψ (z + L)
This gives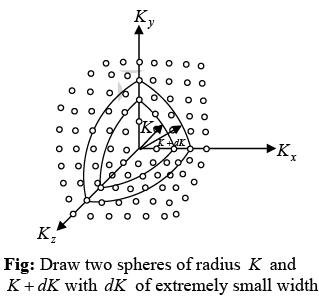
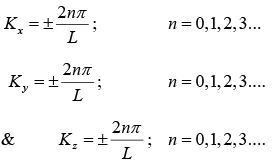
There values can be represented as in figure.
The number of K -states in range K and K + dK is
The density of state is ρ(K)dK = 
|
91 videos|21 docs|25 tests
|
FAQs on Free Electron Theory of Metals - Solid State Physics, Devices & Electronics
| 1. What is the Free Electron Theory of Metals? |  |
| 2. How does the Free Electron Theory explain electrical conductivity in metals? |  |
| 3. What is the significance of the Fermi Level in the Free Electron Theory of Metals? |  |
| 4. How does the Free Electron Theory explain thermal conductivity in metals? |  |
| 5. Can the Free Electron Theory explain all properties of metals? |  |
|
91 videos|21 docs|25 tests
|

|
Explore Courses for Physics exam
|

|



















