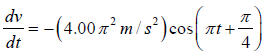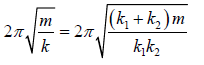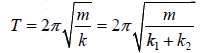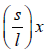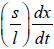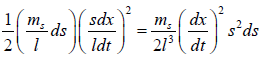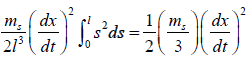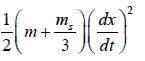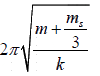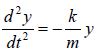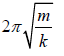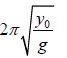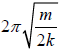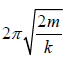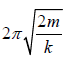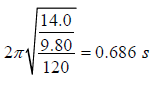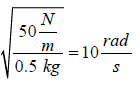Differential Equation for Simple Harmonic Oscillator | Oscillations, Waves & Optics - Physics PDF Download
| Table of contents |

|
| Simple Harmonic Oscillation |

|
| Equations of Motion (Hooke's Law) |

|
| Simple Pendulum |

|
| Compound Pendulum |

|
| The Torsional Pendulum |

|
Simple Harmonic Oscillation
Periodic motion: A motion said to be periodic if, after some set amount of time it returns
to its starting point and begins to repeat its motion.
Example: Earth rotation around sun, Movement of Clock Arm, Electron motion around
nucleus, simple pendulum, and spring loaded mass etc.
Simple Harmonic Motion: Simple harmonic motion is the motion of a mass when it is
subject to the linear restoring force which is proportional but opposite to the displacement
of the mass.
Example: Motion of spring loaded mass, simple pendulum, atomic vibration etc.
Important Terms
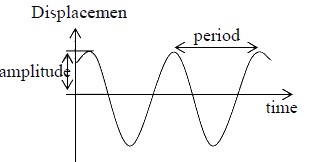
Cycle: The motion of the object from a starting position back to its starting position is called a cycle
Time Period: The time it takes to complete one cycle is called the time period(T ).
Frequency: The frequency ( f ) is the number of cycles per unit time.
Amplitude: The maximum displacement of the mass from its equilibrium position is
called the amplitude ( A) .
Phase: how much of a cycle the system completed (system that begins is in phase zero,
system which completed half a cycle is in phaseπ ).
Equilibrium position: The position about which an object in harmonic motion oscillates;
the center of vibration.
Hooke’s law: law that states that the restoring force applied by a spring is proportional to
the displacement of the spring and opposite in direction.
Restoring force: The force acting on an oscillating object which is proportional to the
displacement and always points toward the equilibrium position.
Equations of Motion (Hooke's Law)
Consider a mass m is attached to the spring, and the other end of the spring is connected
to a rigid support such as a wall. If the system is left at rest at the equilibrium position (x = 0) then there is no net force acting on the mass. However, if the mass is displaced from the equilibrium position, a restoring elastic force opposite to the displacement is exerted by the spring. The equations of motion for a mass on a spring, using Hooke's law is
F = −kx
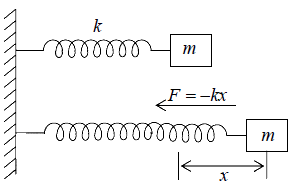
where F is the restoring elastic force exerted by the spring, k is the spring constant, and
x is the displacement from the equilibrium position.
The equation of motion is a second-order linear ordinary differential equation obtained by
means of Newton's second law.
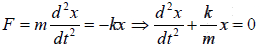
⇒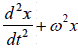 = 0 where ω = √k/m is the Angular frequency of the oscillator.
= 0 where ω = √k/m is the Angular frequency of the oscillator.
We see from this equation that the higher the spring constant k , the stiffer the spring, and the greater the angular frequency of oscillation. A smaller mass will also increase the angular frequency for a particular spring. Solving the differential equation above, a solution which is a sinusoidal function is obtained.
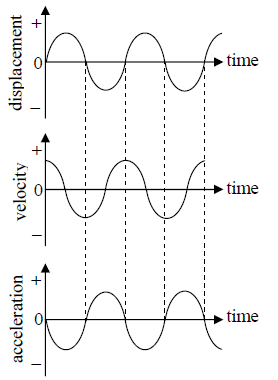
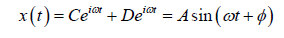
The velocity and acceleration is
v (t) = dx/dt = Aωcos(ωt + φ) = ω√A2 - x2 and a (t) = 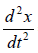 = - Aω2cos(ωt + φ) = -ω2x
= - Aω2cos(ωt + φ) = -ω2x
Then sinceω = 2π f , f = 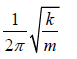
and since T = 1/f where T is the time period, T = 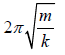
Example 1: An object oscillates with simple harmonic motion along the x - axis. Its
position varies with time according to the equation
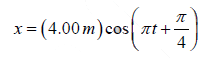
where t is in seconds and the angles in the parentheses are in radians.
(a) Determine the amplitude, frequency, and period of the motion.
(b) Calculate the velocity and acceleration of the object at any time t.
(c) Using the results of part (b), determine the position, velocity, and acceleration of the object at t =1.00 s .
(d) Determine the maximum speed and maximum acceleration of the object.
(e) Find the displacement of the object between t = 0 and t =1.00 s.
(a) Since x = Acos (ωt +φ ) , we see that A = 4.00m andω =π rad / s .
Therefore, f =ω / 2π =π / 2π = 0.500Hz and T =1/ f = 2.00 s .
(b) Differentiating x to find v to find a , we obtain
and a =
(c) At t =1.00 s ,
x =
=
= ( = 4.00m)(−0.707) = −2.83m
v =
= −(4.00π m/ s)(−0.707) = 8.89m/ s
a = −(4.00π2 m/ s2 )(−0.707) = 27.9m/ s2
(d) Since maximum values of the sine and cosine functions are unity. Therefore, v varies between ±4.00π m/ s and a varies between ±4.00π2 m/ s2 .
Thus, vmax = 4.00π m/ s =12.6m/ s and amax = 4.00π2 m/ s2 = 39.5m/ s2
We obtain the same results using the relations vmax =ωA and amax =ω2A where A = 4.00m and ω =π rad / s
(e) The position at t = 0 is
xi =
= (4.00m)(0.707) = 2.83m
In part (c), we found that the position at t =1.00 s is −2.83m; therefore, the displacement between t = 0 and t =1.00s is
Δx = xf − xi = −2.83m −2.83m = − 5.66m
Because the object’s velocity changes sign during the first second, the magnitude of Δx
is not the same as the distance traveled in the first second. (By the time the first second is over, the object has been through the point x = −2.83m once, traveled to x = −4.00 m and come back to x = −2.83m)
Energy of Simple Harmonic Motion
As an object vibrates in harmonic motion, energy is transferred between potential energy
and kinetic energy. If we stretch a spring from its equilibrium (unstretched) position to a certain displacement the work done is equal to the stored potential energy in the spring. If
we release the mass and allow it to begin moving back toward the equilibrium position, the potential energy begins changing into kinetic energy. As the mass passes through the equilibrium position, all of the potential energy has been converted into kinetic energy, and the speed of the mass is maximum. The kinetic energy in turn begins changing into potential energy, until all of the kinetic energy is converted into potential energy at
maximum compression. The compressed spring then accelerates the mass back through
the equilibrium to the original starting position, and the entire process repeats itself. The
total energy of the system remains constant, that is,
Total Energy = Potential Energy + Kinetic Energy = a constant
The kinetic energy K of the system at time t is
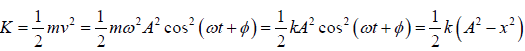
The potential energy is U = 1/2kx2 = 
The total mechanical energy of the system therefore has the constant value
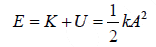
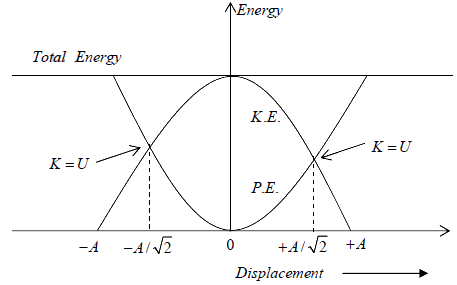
The total energy is constant and has the value is 1/2kA2 . This is also the maximum value
of the potential or the kinetic energy. Thus at the time when P.E. is zero the K.E. is
maximum or vice versa.
Energy vs Position Graph
Energy vs Time Graph
The distribution of energy versus time for S.H.M. is shown in the figure. The P.E.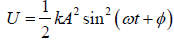 and K.E. is
and K.E. is 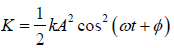 variation with time is shown
variation with time is shown
in figure below.
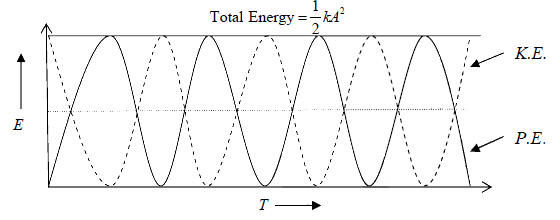
Frequency of energy change in S.H.M.
The energy of the particle in S.H.M. changes periodically from P.E. to K.E. Both U and
K depends upon the square of the displacement x , i.e. each acquires same value twice in
each oscillation. Thus the frequency of energy change is twice the frequency of
oscillation.
Time average of kinetic and potential energy
Time average of kinetic energy 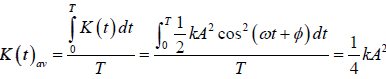
Time average of potential energy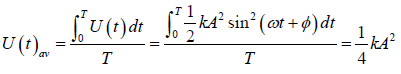
Thus the time average of kinetic energy is equal to the time average of the potential
energy which is half the total energy.
Position average of kinetic and potential energy
Position average of kinetic energy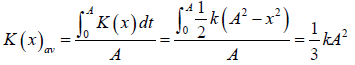
Position average of potential energy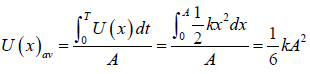
Thus the position average of kinetic energy is equal to the twice of the position average
of the potential energy.
Mass Loaded Spring System
Example 2: Find the time period for the arrangement for the following mass loaded spring having spring constant k1 and k2 .
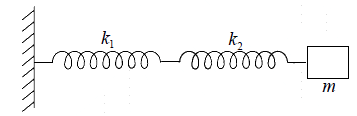
Let x be the displacement of m from its equilibrium position at an instant, and
x1, x2 is extension in the length of springs k1 and k2 respectively.
Thus x = x1 + x2
The restoring force in k1 and k2 will be the same. By Hooke’s law we have
F = -k1x1 = -k2x2
x =
⇒ F =
= -kx
Thus the force constant of the system is k =
.
Hence the time period is T =
Example 3: Find the time period for the arrangement for the following mass loaded spring having spring constant k1 and k2 .
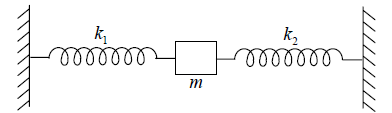
During oscillation one spring stretched and other compressed and vice versa.
Let x be the displacement of mass m from its equilibrium distance, and this is also the
compression and expansion in the springs k1 and k2 . The restoring force developed in the two springs is F1 = −k1x and F2 = −k2x . F1 and F2 act on the mass in the same direction
F = F1 + F2 = −k1x − k2x = − (k1 + k2)x = −kx
Thus the force constant of the system is (k1 + k2), and the time period is
Example 4: Determine the time period of the system of mass m attached with spring of mass ms (ms << m) and spring constant k .
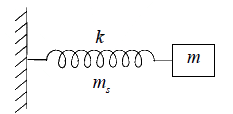
If ms << m , then the spring will stretch uniformly along its length. Let l be the
length of the spring, its mass per unit length will be ms/l. Let us consider an element of
length ds at a distance s from the fixed end of the string. The mass of this element
is
. Let x be the instantaneous displacement of m .
The displacement of a element of spring =
The instantaneous velocity of element =
The instantaneous kinetic energy of element =
The total kinetic energy of the uniform spring
The total kinetic energy of the whole system is K =
This shows the effective mass of the system is
.
Hence the time period is T =
Example 5: Find the time period for the arrangement for the following mass loaded
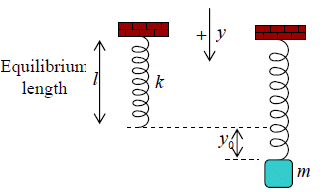
vertical spring having spring constant k .
Consider l be the length of the spring hanging vertically. When mass m attached to the lower end, it’s length extended by y0 . By Hooke’s law the restoring
force is F = −ky0 .
The other force acting on the mass is its weight +mg (downward). Thus the total force on m is 0 −ky + mg .
Since mass has no acceleration, the total force on mass m is zero,
−ky0 + mg = 0 ⇒ y0 = mg / k
When the body is pulled through a small distance y from the equilibrium position and
released, it start oscillating with SHM, since the restoring force is F = −ky , imparting an acceleration of
is given by
Which is a equation of SHM whose time period is T =
It can also be written as T =
Example 6: Find the time period of the following sets of mass loaded springs hanged vertically.
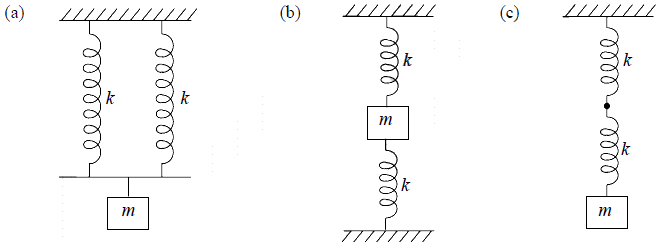
(a) Since both springs are in parallel combination. The resultant spring constant of the
system is k′ = k + k = 2k . Thus the time period is T =
(b) Since both springs are in series. The resultant spring constant of the system is
. Thus the time period is T =
(c) In this case also springs are in series. Thus time period of the system is T =
Example 7: A block weighing14.0 N , which can slide without friction on an incline at
angle θ = 40.00 , is connected to the top of the incline by a massless spring of unstretched length 0.450 m and spring constant120 N/m.
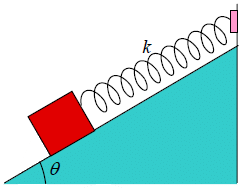
(a) How far from the top of the incline is the block's equilibrium point?
(b) If the block is pulled slightly down the incline and released, what is the period of the resulting oscillations?
(a) The equilibrium position when the block is gently lowered until forces balance. If the
amount spring is stretched is x , then we examine force-components along the incline
surface and find
kx = mg sinθ ⇒ x =
= 0.0750 m
At equilibrium, the distance from the top of the incline is therefore
(0.450 + 0.075)m = 0.525 m.
(b) Just as with a vertical spring, the effect of gravity (or one of its components) is simply to shift the equilibrium position; it does not change the characteristics (such as the period) of simple harmonic motion.
T =
Example 8: A spring of constant k = 100 N/m hangs at its natural length from a fixed stand. A mass of 3 kg is hung on the end of the spring, and slowly let down until the spring and mass hang at their new equilibrium position.
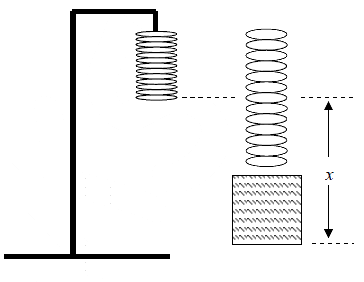
(a) Find the value of the quantity x in the figure above. The spring is now pulled down an additional distance x and released from rest.
(b) What is the potential energy in the spring at this distance?
(c) What is the speed of the mass as it passes the equilibrium position?
(d) How high above the point of release will the mass rise?
(e) What is the period of oscillation for the mass?
(a) As it hangs in equilibrium, the upward spring force must be equal and opposite to the downward weight of the block.
Fs = mg and kx = mg ⇒ x = mg/k =
= 0.3 m
(b) The potential energy in the spring is related to the displacement from equilibrium
position by the equation
U = 1/2kx2 =
= 4.5J
(c) Since energy is conserved during the oscillation of the mass, the kinetic energy of the mass as it passes through the equilibrium position is equal to the potential energy at the amplitude. Thus,
K = U = 1/2mv2 ⇒ v =
= 1.7 m/s
(d) Since the amplitude of the oscillation is 0.3 m , it will rise to 0.3 m above the
equilibrium position.
(e) T =
=
= 1.1s
Example 9: A mass of 0.5 kg oscillates on the end of a spring on a horizontal surface with negligible friction according to the equation x = Acos(ω t). The graph of F vs x for this motion is shown below.
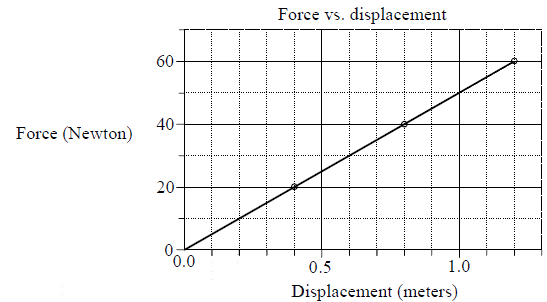
The last data point corresponds to the maximum displacement of the mass.
Determine the
(a) Angular frequency ω of the oscillation,
(b) Frequency f of oscillation,
(c) Amplitude of oscillation,
(d) Displacement from equilibrium position (x = 0) at a time of 2s .
(a) When we looked at this graph k =
⇒ω =
=
(b) f =
= 1.6 Hz
(c) The amplitude corresponds to the last displacement on the graph, A =1.2 m.
(d) x = Acos(ωt ) = (1.2 m)cos [(10 rad / s)(2 s)] = 0.5m
Simple Pendulum
A simple pendulum is an idealized system containing of a massless inextensible string,
fixed rigidly at one end, having a point mass at the other end.
A mass m suspended by a light string of length L from a fixed point. When the mass is displaced slightly from its equilibrium position and released, it oscillates in a vertical plane under gravity. Let θ be the angular displacement of the pendulum. The force acting on m is mg . This force can be resolved into two components, a radial component mg cosθ along the string and tangential component mg sinθ at right angle to it. The tangential component is the restoring force.
Thus F = −mg sinθ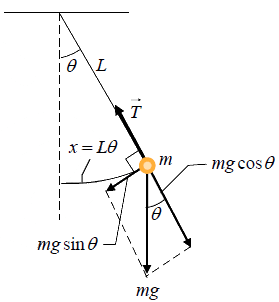
Using Newton’s law, we get 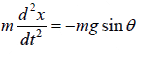
For small angles of oscillations sinθ = x/L, is governed by 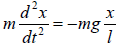
The frequency ( f ) and the period(T ) of the pendulum in this case are given by:
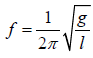 and
and 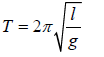
Therefore, the simple pendulum has the following properties
(i) The period of a pendulum is independent of its own mass and the amplitude of the
oscillation.
(ii) The period of the pendulum is depends on its length.
Large Amplitude: When the amplitude of motion of the simple pendulum is large, the
approximation sinq = q does not hold and the pendulum deviates from the simple
harmonic behavior. Then the time period T = 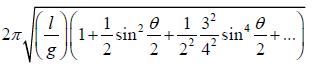
Thus with increasing amplitude the time period increases.
Compound Pendulum
A compound pendulum is a rigid body, of any shape, capable of oscillating about a horizontal axis passing through it.
Let m be the mass of the body and l be the distance of C from O. When body displaced by an angle θ with the vertical, at this instant the moment of its weight mg about the axis of oscillation through O is mg (l sinθ ) .
This is the restoring torque which brings the body to its equilibrium position.
Thus τ = −mgl sinθ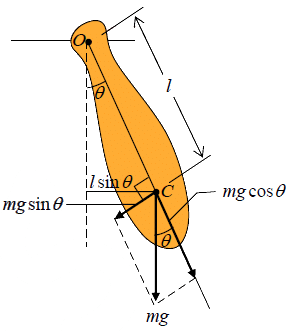
For small angle, we have; τ = −mglθ
If I is the moment of inertia of the pendulum about the axis of suspensionO, the torque
is also equal to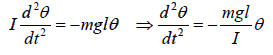
Thus the time period is T = 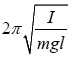
It is sometime more useful to write the time period in term of radius of gyration of
pendulum. If we write the moment of inertia about a parallel axis through C , then
I = mk2 +ml2 = m(k2 + l2 )
Thus the time period is
T = 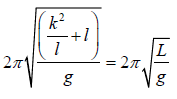
Here L is called the “length of the equivalent simple pendulum.”
The Torsional Pendulum
A torsional pendulum consist of a heavy body such as disc or cylinder be hung by a long
and thin vertical wire from a rigid support. If the disc is turned in the horizontal plane and
then released, due to wire elasticity, it executes a torsional oscillation about the wire as a
axis.
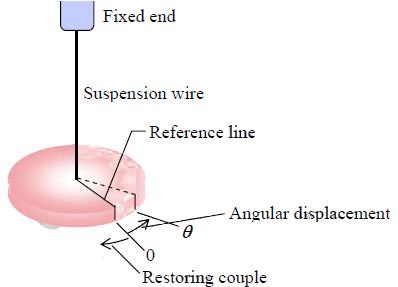
If the disc is turned by an angleθ , the wire is also twisted by same angle. A restoring
torque (−τθ ) produced which brings the pendulum back to its original position. If I is
the moment of inertia of the disc about the wire, then the torque acting on the disc must
be equal to the product of the moment of inertia I and the angular acceleration.
Thus
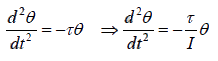
The time period of the oscillation is T = 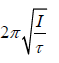
|
54 videos|22 docs|14 tests
|
FAQs on Differential Equation for Simple Harmonic Oscillator - Oscillations, Waves & Optics - Physics
| 1. What is a simple harmonic oscillator? |  |
| 2. How can the equations of motion be derived using Hooke's Law? |  |
| 3. What is a simple pendulum? |  |
| 4. How does a compound pendulum differ from a simple pendulum? |  |
| 5. What is a torsional pendulum? |  |