Blackbody Radiation, Photoelectric Effect & Compton Effect | Modern Physics PDF Download
Black Body Radiation
A black body is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence.
A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black body radiation.
When an object is heated, it radiated electromagnetic energy as result of thermal agitation of electrons in its surface .the intensity of radiation depends on its frequency and on the temperature, the light it emits ranges over the entire spectrum.
An object in thermal equilibrium with its surrounding radiates as much energy it absorbers. A Black body is perfect absorber as well perfect emitter of radiation.
Wien’s Distribution Law
Wien's approximation (also sometimes called Wien's law or the Wien distribution law) is a law of used to describe the spectrum of thermal radiation (frequently called the blackbody function). The equation does accurately describe the short wavelength (high frequency) spectrum of thermal emission from objects, but it fails to accurately fit the experimental data for long wavelengths (low frequency) emission.
The law may be written as
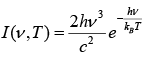
where I (v, T) is the amount of energy per unit surface area per unit time per unit solid angle per unit frequency emitted at a frequency v.
T is the temperature of the black body, h is planks constant, c is the speed of light, kB is Boltzmann’s constant.
This equation may also be written as
Where I (λ, T) is the amount of energy per unit surface area per unit time per unit solid angle per unit wavelength emitted at a wavelength λ.
Rayleigh’s Energy Density Distribution
Total energy per unit volume in the cavity in the frequency interval from v to v + dv is given by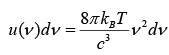
But above relation does not describe the experimental trend at higher frequency. The equation does accurately describe the long wavelength (short frequency) spectrum of thermal emission from objects, but it fails to accurately fit the experimental data for short wavelengths (high frequency) emission.
In term of wavelength the energy density is given by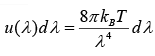
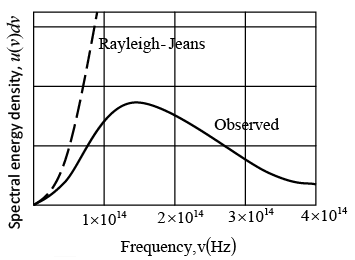 Comparison of the Rayleigh-Jeans formula for the spectrum of the radiation from a blackbody at 1500 K with the observed spectrum. The discrepancy is known as the ultraviolet catastrophe because it increases with increase frequency. This failure of classical physics led Planck to the discovery that radiation is emitted in quanta whose energy is hv.
Comparison of the Rayleigh-Jeans formula for the spectrum of the radiation from a blackbody at 1500 K with the observed spectrum. The discrepancy is known as the ultraviolet catastrophe because it increases with increase frequency. This failure of classical physics led Planck to the discovery that radiation is emitted in quanta whose energy is hv.
Planks Radiation Formula
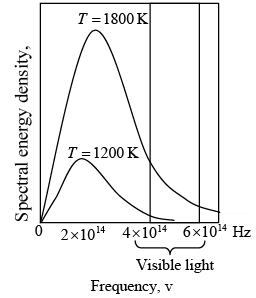 Blackbody spectra. The spectral distribution of energy in the radiation depends only on the temperature of the body.
Blackbody spectra. The spectral distribution of energy in the radiation depends only on the temperature of the body.
With assumption that radiation has discrete energy analogous to oscillator which is given by En = nhv where n = 0,1, 2...
Total energy per unit volume in the cavity in the frequency interval from v to v + dv is given by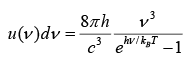
where for high frequency (low wavelength) ii will approach to Wien’s distribution and for low frequency(high wavelength) it will approach to Raleigh- Jeans formula.
Photo Electric Effect
In the photoelectric effect, electrons are emitted from solids, liquids or gases when they absorb energy from light. Electrons emitted in this manner may be called photoelectrons.
The photoelectric effect requires photons with energies from a few electron volts to over 1MeV in high atomic number elements. Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons and influenced the formation of the concept of wave-particle duality. It also led to Max Planck's discovery of quantized energy and the Planck Relation (E = hv), which links a photon's frequency with its energy. The factor h is known as the Planck constant.
Experimental observation
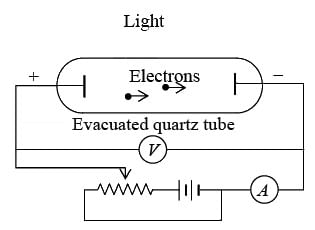 Experimental observation of the photoelectric effect
Experimental observation of the photoelectric effect
- Because electromagnetic wave is concentrated in photons and not spread out, there should be no delay in the emission of photoelectron as light falls on the matter.
- All photons of frequency v have the same energy so changing the intensity of monochromatic light beam will change the number of photoelectrons not their energies.
- The higher the frequency v, the greater the photon energy (E = hv) and so the more energy the photoelectron have.
Threshold Frequency and Work Function
For a given metal, there exists a certain minimum frequency of incident radiation below which no photoelectrons are emitted. This frequency is called the threshold frequency or critical frequency (v0). There must be minimum energy ϕ for an electron to escape from a particular metal surface; this energy is known as work function which is given by ϕ = hv0.
Einstein equation of photoelectric effect
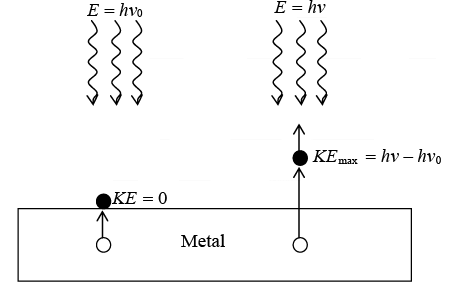 If the energy hv0 (the work function of the surface) is needed to remove an electron from a metal surface, the maximum electron kinetic energy will be hv - hv0 when light of frequency v is directed at the surface.
If the energy hv0 (the work function of the surface) is needed to remove an electron from a metal surface, the maximum electron kinetic energy will be hv - hv0 when light of frequency v is directed at the surface.
When a metal is irradiated with light, electron may get emitted. Kinetic energy of photoelectron observed when irradiated with a light of frequency v > vo, where vo is threshold frequency is given by KEmax where KEmax = hv - hv0
This maximum kinetic energy is equivalent to Stopping potential Vs which is energy required to stop electron which contain maximum kinetic energy.
Then eVs = hv0 which is known as Einstein equation.
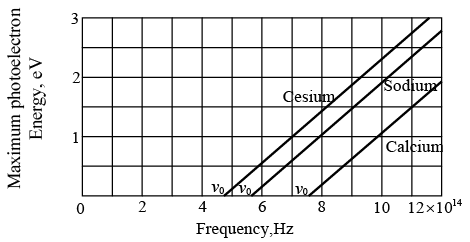 Maximum photoelectron kinetic energy KEmax versus frequency of incident light for three metal surfaces.
Maximum photoelectron kinetic energy KEmax versus frequency of incident light for three metal surfaces.
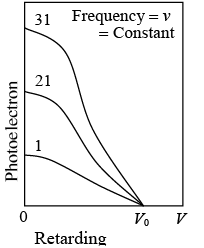 Photoelectron current is proportional to light intensity I for all retarding voltages. The extinction voltage v0 which corresponds to the maximum photoelectron energy, is the same for all intensities of light of the same frequency v.
Photoelectron current is proportional to light intensity I for all retarding voltages. The extinction voltage v0 which corresponds to the maximum photoelectron energy, is the same for all intensities of light of the same frequency v.
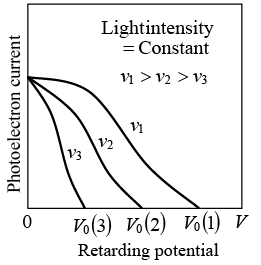 The extinction voltage V0, and hence the maximum photoelectron energy, depends on the frequency of the light. When the retarding potential is V = 0, the photoelectron current is the same for light of a given intensity regardless of its frequency.
The extinction voltage V0, and hence the maximum photoelectron energy, depends on the frequency of the light. When the retarding potential is V = 0, the photoelectron current is the same for light of a given intensity regardless of its frequency.
Example 1: When light of a given wavelength is incident on metallic surface ,the stopping potential for the photoelectrons is 3.2V. if a second light source whose wavelength is double that of the first is used , the stopping potential drop to 0.8V.
(a) Calculate the wavelength of first radiation
(b) The work function and the cutoff frequency of the metal.
Let us assume work function of metal is given by ϕ.
For wavelength λ1 and λ2 stopping potential is given by Vs1 = 3.2V and Vs2 = 0.8 where λ2 = 2λ1.
Solving equation (i) and (ii)
(b) Eliminating λ1 from (i) and (ii) ϕ = e(Vs1 - 2Vs2) = 3.84 x 10-19 J
Cutoff frequency v = ϕ/h = 5.8 x 1014
Example 2: Ultraviolet light of wavelength 350 nm and intensity 1 W /m2 is directed at potassium surface.
(a) Find the maximum kinetic of photoelectrons
(b) If 0.5% of incident photons produce photoelectrons, how many are emitted per second if the potassium surface has area of 1cm2
It is given hc = 1.24 x 10-6 eV .m and work function of potassium is 2.2eV
(a) Energy of photon is
Maximum kinetic energy is given by
(b) No. of photon that reach the surface per second is given by
No of photo electron is ne = np x 0.005 = 8.8 x 1011 photo electrons/second.
Example 3: In a photoelectric experiment, it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300 nm to 400 nm. Calculate the value of the Planck constant from these data.
The maximum kinetic energy of a photoelectron is
and the stopping potential is
If V1 ,V2 are the stopping potentials at wavelengths λ1 and λ2 respectively,
Example 4: A monochromatic light of wavelength λ is incident on an isolated metallic sphere of radius a . The threshold wavelength is λ0 which is larger than λ. Find the number of photoelectrons emitted before the emission of photoelectrons will stop.
As the metallic sphere is isolated, it becomes positively charged when electrons are ejected from it. There is an extra attractive force on the photoelectrons. If the potential of the sphere is raised to V, the electrons should have a minimum energy φ + eV to be able to come out. Thus, emission of photoelectrons will stop when
The charge on the sphere needed to take its potential to V is Q = (4πε0a)V.
The number of electrons emitted is, therefore,
Compton Scattering
Compton scattering is an inelastic scattering of a photon by a free charged particle, usually an electron. It results in a decrease in energy (increase in wavelength) of the photon (which may be an X-ray or gamma ray photon), called the Compton Effect. Part of the energy of the photon is transferred to the scattering electron. Inverse Compton scattering also exists, in which a charged particle transfers part of its energy to a photon. This experiment give experimental prove of particle aspect of photon (light).
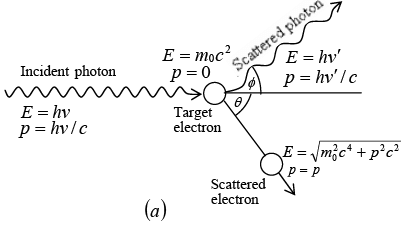
The scattering of photon of energy hv by an electron rest mass m0. After scattering photon scattered at angle ϕ and electron scattered at angle θ. The scattered photon have energy hv' and electron have energy E.
The vector diagram of the momenta and their components of the incident and scattered photon and scattered electron shown in vector diagram From the conservation of energy
loss in photon energy = gain in electron energy hv - hv' = KE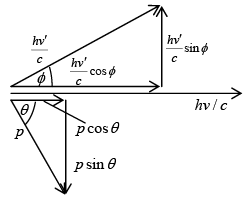 The momentum of photon is given p = E/c = hv/c
The momentum of photon is given p = E/c = hv/c
From conservation of momentum in x direction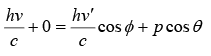
Conservation of momentum in y direction
From above two equation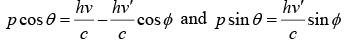
Squaring and adding one will get p2c2 = (hv)2 - 2(hv)(hv')cosϕ + (hv')2 …….(i)
Kinetic energy of electron is given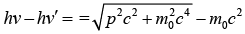
p2 c2 = (hv)2 - 2(hv)(hv') + (hv')2 + 2m0c2 (hv - hv')…….(ii)
Equating equation (i) and (ii) 2m0c2(hv - hv') = 2 (hv)(hv')(1 - cos ϕ)

Value of Δλ = λ' - λ for different scattering angle ϕ shown in figure
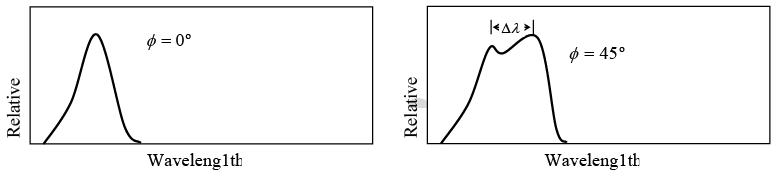
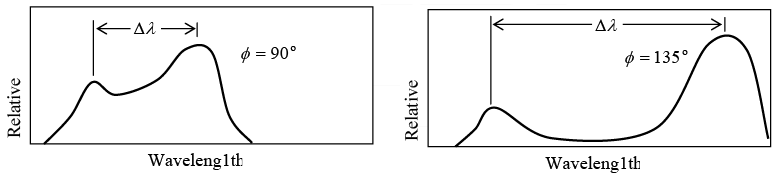
Example 5: X-ray of wavelength10.0 pm are scattered from a target
(a) Find the wavelength of the X-rays scattered through 450
(b) Find the maximum wavelength present in the scattered X-rays
(c) Find the maximum kinetic energy of the recoil electrons.
It is given that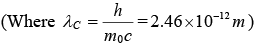
(a) λ' - λ = λc (1 - cos(ϕ) λ' = λ + λc(1 - cosϕ) =10.7pm
(b) λ' = λ + λc (1 - cos (ϕ) is maximum for ϕ = π λ'max = λ + 2λc = 14.9pm
(c) Kinetic energy of electron is given by
For maximum kinetic energy
Example 6: In a Compton scattering prove that 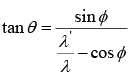 where θ and ϕ are the angle of recoil of electron and scattering angle of photon.
where θ and ϕ are the angle of recoil of electron and scattering angle of photon.
From conservation of momentum
We will get
Example 7: Show that the maximum kinetic energy transferred to proton when hit by photon of energy hv is 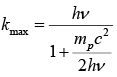
Kinetic energy KE = hv - hv'
For maximum kinetic energy
Example 8: High energy photons (γ - rays) are scattered from electrons initially at rest. Assume the photons are backscattered and their energies are much larger than the electron’s restmass energy, E ≫ mec2.
(a) Calculate the wavelength shift
(b) Show that the energy of the scattered photons is half the rest mass energy of the electron, regardless of the energy of the incident photons.
(c) Calculate the electron’s recoil kinetic energy if the energy of the incident photons is 150 MeV.
(a) In the case where the photons backscatter (i.e., θ = π), the wave length shift becomes
The numerical value of Δλ is easy to obtain by making use of hc = 197.33 x 10-15 MeV m and mec2 = 0.511 MeV:
(b) Since the energy of the scattered photons E' is related to the wavelength λ' by E' = hc/λ' , equation) yields
whereis the energy of the incident photons. If E ≫ mec2 we can approximate by
(c) If E = 15 MeV the kinetic energy of the recoiling electrons can be obtained from the conservation of energy
Ke = E - E' ≈ 150 MeV - 0.25 MeV = 149.75 MeV
|
37 videos|16 docs|19 tests
|
FAQs on Blackbody Radiation, Photoelectric Effect & Compton Effect - Modern Physics
| 1. What is black body radiation? |  |
| 2. What is the photoelectric effect? |  |
| 3. How does black body radiation relate to the photoelectric effect? |  |
| 4. What is the Compton effect? |  |
| 5. How are black body radiation, the photoelectric effect, and the Compton effect relevant to the IIT JAM exam? |  |

|
Explore Courses for Physics exam
|

|























 is the energy of the incident photons. If E ≫ mec2 we can approximate by
is the energy of the incident photons. If E ≫ mec2 we can approximate by 

















