Sorting Algorithms- 3 | Algorithms - Computer Science Engineering (CSE) PDF Download
Insertion Sort
Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
Algorithm
To sort an array of size n in ascending order:
- Iterate from arr[1] to arr[n] over the array.
- Compare the current element (key) to its predecessor.
- If the key element is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.
Example: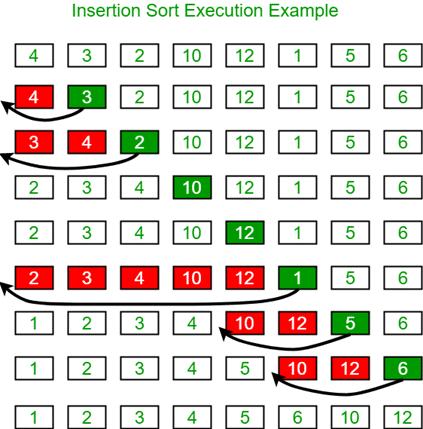
Another Example:
12, 11, 13, 5, 6
Let us loop for i = 1 (second element of the array) to 4 (last element of the array)
i = 1. Since 11 is smaller than 12, move 12 and insert 11 before 12
11, 12, 13, 5, 6
i = 2. 13 will remain at its position as all elements in A[0..I-1] are smaller than 13
11, 12, 13, 5, 6
i = 3. 5 will move to the beginning and all other elements from 11 to 13 will move one position ahead of their current position.
5, 11, 12, 13, 6
i = 4. 6 will move to position after 5, and elements from 11 to 13 will move one position ahead of their current position.
5, 6, 11, 12, 13
- C++
// C++ program for insertion sort
#include <bits/stdc++.h>
using namespace std;
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
/* Driver code */
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}
// This is code is contributed by rathbhupendra - C
// C program for insertion sort
#include <math.h>
#include <stdio.h>
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)
{
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
void printArray(int arr[], int n)
{
int i;
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
/* Driver program to test insertion sort */
int main()
{
int arr[] = { 12, 11, 13, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
} - Java
// Java program for implementation of Insertion Sort
class InsertionSort {
/*Function to sort array using insertion sort*/
void sort(int arr[])
{
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
/* A utility function to print array of size n*/
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver method
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6 };
InsertionSort ob = new InsertionSort();
ob.sort(arr);
printArray(arr);
}
} /* This code is contributed by Rajat Mishra. */ - Python
# Python program for implementation of Insertion Sort
# Function to do insertion sort
def insertionSort(arr):
# Traverse through 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
# Move elements of arr[0..i-1], that are
# greater than key, to one position ahead
# of their current position
j = i-1
while j >= 0 and key < arr[j] :
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Driver code to test above
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
for i in range(len(arr)):
print ("% d" % arr[i])
# This code is contributed by Mohit Kumra - C#
// C# program for implementation of Insertion Sort
using System;
class InsertionSort {
// Function to sort array
// using insertion sort
void sort(int[] arr)
{
int n = arr.Length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
// Move elements of arr[0..i-1],
// that are greater than key,
// to one position ahead of
// their current position
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print
// array of size n
static void printArray(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.Write("\n");
}
// Driver Code
public static void Main()
{
int[] arr = { 12, 11, 13, 5, 6 };
InsertionSort ob = new InsertionSort();
ob.sort(arr);
printArray(arr);
}
}
// This code is contributed by ChitraNayal. - PHP
<?php
// PHP program for insertion sort
// Function to sort an array
// using insertion sort
function insertionSort(&$arr, $n)
{
for ($i = 1; $i < $n; $i++)
{
$key = $arr[$i];
$j = $i-1;
// Move elements of arr[0..i-1],
// that are greater than key, to
// one position ahead of their
// current position
while ($j >= 0 && $arr[$j] > $key)
{
$arr[$j + 1] = $arr[$j];
$j = $j - 1;
}
$arr[$j + 1] = $key;
}
}
// A utility function to
// print an array of size n
function printArray(&$arr, $n)
{
for ($i = 0; $i < $n; $i++)
echo $arr[$i]." ";
echo "\n";
}
// Driver Code
$arr = array(12, 11, 13, 5, 6);
$n = sizeof($arr);
insertionSort($arr, $n);
printArray($arr, $n);
// This code is contributed by ChitraNayal.
?> - Javascript
<script>
// Javascript program for insertion sort
// Function to sort an array using insertion sort
function insertionSort(arr, n)
{
let i, key, j;
for (i = 1; i < n; i++)
{
key = arr[i];
j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// A utility function to print an array of size n
function printArray(arr, n)
{
let i;
for (i = 0; i < n; i++)
document.write(arr[i] + " ");
document.write("<br>");
}
// Driver code
let arr = [12, 11, 13, 5, 6 ];
let n = arr.length;
insertionSort(arr, n);
printArray(arr, n);
// This code is contributed by Mayank Tyagi
</script>
Output:
5 6 11 12 13
Time Complexity: O(n^2)
Auxiliary Space: O(1)
Boundary Cases: Insertion sort takes maximum time to sort if elements are sorted in reverse order. And it takes minimum time (Order of n) when elements are already sorted.
Algorithmic Paradigm: Incremental Approach
Sorting In Place: Yes
Stable: Yes
Online: Yes
Uses: Insertion sort is used when number of elements is small. It can also be useful when input array is almost sorted, only few elements are misplaced in complete big array.
What is Binary Insertion Sort?
We can use binary search to reduce the number of comparisons in normal insertion sort. Binary Insertion Sort uses binary search to find the proper location to insert the selected item at each iteration. In normal insertion, sorting takes O(i) (at ith iteration) in worst case. We can reduce it to O(logi) by using binary search. The algorithm, as a whole, still has a running worst case running time of O(n^2) because of the series of swaps required for each insertion. Refer this for implementation.
How to implement Insertion Sort for Linked List?
Below is simple insertion sort algorithm for linked list.
- Create an empty sorted (or result) list
- Traverse the given list, do following for every node.
......a) Insert current node in sorted way in sorted or result list. - Change head of given linked list to head of sorted (or result) list.
|
81 videos|113 docs|34 tests
|
















