Sorting Algorithms- 5 | Algorithms - Computer Science Engineering (CSE) PDF Download

Counting Sort

Counting sort is a sorting technique based on keys between a specific range. It works by counting the number of objects having distinct key values (kind of hashing). Then doing some arithmetic to calculate the position of each object in the output sequence.
Let us understand it with the help of an example.
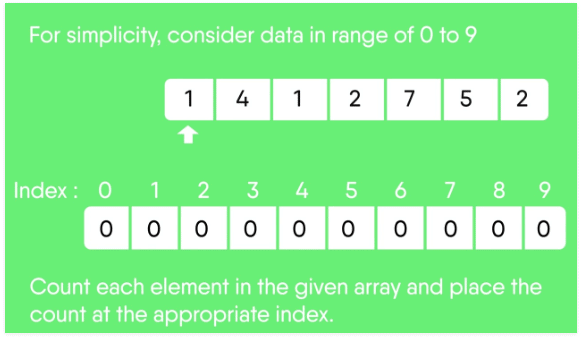
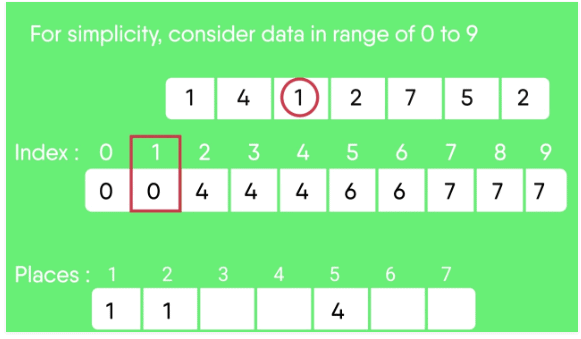
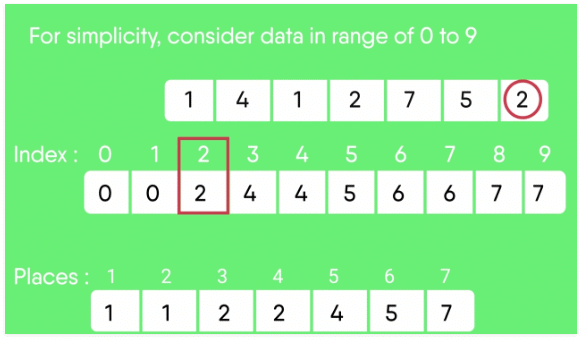
For simplicity, consider the data in the range 0 to 9.
Input data: 1, 4, 1, 2, 7, 5, 2
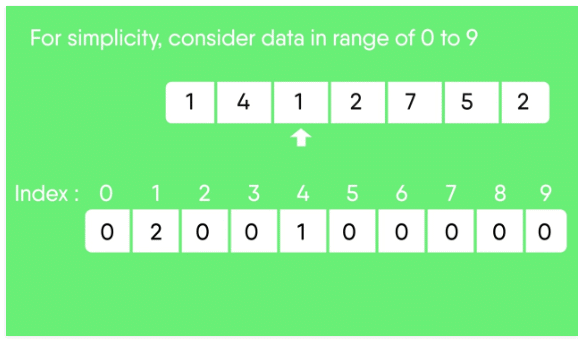
1. Take a count array to store the count of each unique object.
  Index:     0  1  2  3  4  5  6  7  8  9
  Count:     0  2  2  0   1  1  0  1  0  0
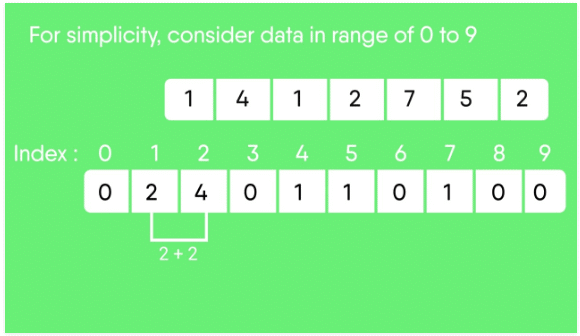
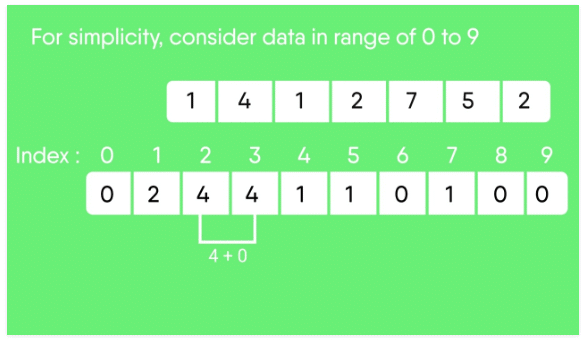
2. Modify the count array such that each element at each index stores the sum of previous counts.
  Index:     0  1  2  3  4  5  6  7  8  9
  Count:     0  2  4  4  5  6  6  7  7  7
The modified count array indicates the position of each object in the output sequence.
3. Output each object from the input sequence followed by decreasing its count by 1.
  Process the input data: 1, 4, 1, 2, 7, 5, 2. Position of 1 is 2.
  Put data 1 at index 2 in output. Decrease count by 1 to place
  next data 1 at an index 1 smaller than this index.

Following is implementation of counting sort:

• C++
  // C++ Program for counting sort
  #include <bits/stdc++.h>
  #include <string.h>
  using namespace std;
  #define RANGE 255
  // The main function that sort
  // the given string arr[] in
  // alphabetical order
  void countSort(char arr[])
  {
      // The output character array
      // that will have sorted arr
      char output[strlen(arr)];
      // Create a count array to store count of individual
      // characters and initialize count array as 0
      int count[RANGE + 1], i;
      memset(count, 0, sizeof(count));
      // Store count of each character
      for (i = 0; arr[i]; ++i)
          ++count[arr[i]];
      // Change count[i] so that count[i] now contains actual
      // position of this character in output array
      for (i = 1; i <= RANGE; ++i)
          count[i] += count[i - 1];
      // Build the output character array
      for (i = 0; arr[i]; ++i) {
          output[count[arr[i]] - 1] = arr[i];
          --count[arr[i]];
      }
      /*
      For Stable algorithm
      for (i = sizeof(arr)-1; i>=0; --i)
      {
          output[count[arr[i]]-1] = arr[i];
          --count[arr[i]];
      }
      For Logic : See implementation
      */
      // Copy the output array to arr, so that arr now
      // contains sorted characters
      for (i = 0; arr[i]; ++i)
          arr[i] = output[i];
  }
  // Driver  code
  int main()
  {
      char arr[] = "geeksforgeeks";
      countSort(arr);
      cout << "Sorted character array is " << arr;
      return 0;
  }
  // This code is contributed by rathbhupendra
• C
  // C Program for counting sort
  #include <stdio.h>
  #include <string.h>
  #define RANGE 255
  // The main function that sort the given string arr[] in
  // alphabatical order
  void countSort(char arr[])
  {
      // The output character array that will have sorted arr
      char output[strlen(arr)];
      // Create a count array to store count of inidividul
      // characters and initialize count array as 0
      int count[RANGE + 1], i;    memset(count, 0, sizeof(count));
      // Store count of each character
      for (i = 0; arr[i]; ++i)
          ++count[arr[i]];
      // Change count[i] so that count[i] now contains actual
      // position of this character in output array
      for (i = 1; i <= RANGE; ++i)
          count[i] += count[i - 1];
      // Build the output character array
      for (i = 0; arr[i]; ++i) {
          output[count[arr[i]] - 1] = arr[i];
          --count[arr[i]];
      }
      /*
       For Stable algorithm
       for (i = sizeof(arr)-1; i>=0; --i)
      {
          output[count[arr[i]]-1] = arr[i];
          --count[arr[i]];
      }
      For Logic : See implementation
      */
      // Copy the output array to arr, so that arr now
      // contains sorted characters
      for (i = 0; arr[i]; ++i)
          arr[i] = output[i];
  }
  // Driver program to test above function
  int main()
  {
      char arr[] = "geeksforgeeks"; //"applepp";
      countSort(arr);
      printf("Sorted character array is %sn", arr);
      return 0;
  }
• Java
  // Java implementation of Counting Sort
  class CountingSort {
      void sort(char arr[])
      {
          int n = arr.length;
          // The output character array that will have sorted arr
          char output[] = new char[n];
         // Create a count array to store count of inidividul
          // characters and initialize count array as 0
          int count[] = new int[256];
          for (int i = 0; i < 256; ++i)
              count[i] = 0;
          // store count of each character
          for (int i = 0; i < n; ++i)
              ++count[arr[i]];
          // Change count[i] so that count[i] now contains actual
          // position of this character in output array
          for (int i = 1; i <= 255; ++i)
              count[i] += count[i - 1];
          // Build the output character array
          // To make it stable we are operating in reverse order.
          for (int i = n - 1; i >= 0; i--) {
              output[count[arr[i]] - 1] = arr[i];
              --count[arr[i]];
          }
          // Copy the output array to arr, so that arr now
          // contains sorted characters
          for (int i = 0; i < n; ++i)
              arr[i] = output[i];
      }
      // Driver method
      public static void main(String args[])
      {
          CountingSort ob = new CountingSort();
          char arr[] = { 'g', 'e', 'e', 'k', 's', 'f', 'o',
                         'r', 'g', 'e', 'e', 'k', 's' };
          ob.sort(arr);
          System.out.print("Sorted character array is ");
          for (int i = 0; i < arr.length; ++i)
              System.out.print(arr[i]);
      }
  }
  /*This code is contributed by Rajat Mishra */
• Python3
  # Python program for counting sort
  # The main function that sort the given string arr[] in
  # alphabetical order
  def countSort(arr):
      # The output character array that will have sorted arr
      output = [0 for i in range(len(arr))]
      # Create a count array to store count of inidividul
      # characters and initialize count array as 0
      count = [0 for i in range(256)]
      # For storing the resulting answer since the
      # string is immutable
      ans = ["" for _ in arr]
      # Store count of each character
      for i in arr:
          count[ord(i)] += 1
      # Change count[i] so that count[i] now contains actual
      # position of this character in output array
      for i in range(256):
          count[i] += count[i-1]
      # Build the output character array
      for i in range(len(arr)):
          output[count[ord(arr[i])]-1] = arr[i]
          count[ord(arr[i])] -= 1
      # Copy the output array to arr, so that arr now
      # contains sorted characters
      for i in range(len(arr)):
          ans[i] = output[i]
      return ans
  # Driver program to test above function
  arr = "geeksforgeeks"
  ans = countSort(arr)
  print("Sorted character array is % s" %("".join(ans)))
  # This code is contributed by Nikhil Kumar Singh
• C#
  // C# implementation of Counting Sort
  using System;
  class GFG {
      static void countsort(char[] arr)
      {
          int n = arr.Length;
          // The output character array that
          // will have sorted arr
          char[] output = new char[n];
          // Create a count array to store
          // count of inidividul characters
          // and initialize count array as 0
          int[] count = new int[256];
          for (int i = 0; i < 256; ++i)
              count[i] = 0;
          // store count of each character
          for (int i = 0; i < n; ++i)
              ++count[arr[i]];
          // Change count[i] so that count[i]
          // now contains actual position of
          // this character in output array
          for (int i = 1; i <= 255; ++i)
              count[i] += count[i - 1];
          // Build the output character array
          // To make it stable we are operating in reverse order.
          for (int i = n - 1; i >= 0; i--) {
              output[count[arr[i]] - 1] = arr[i];
              --count[arr[i]];
          }
           // Copy the output array to arr, so
          // that arr now contains sorted
          // characters
          for (int i = 0; i < n; ++i)
              arr[i] = output[i];
      }
      // Driver method
      public static void Main()
      {
          char[] arr = { 'g', 'e', 'e', 'k', 's', 'f', 'o',
                         'r', 'g', 'e', 'e', 'k', 's' };
          countsort(arr);
          Console.Write("Sorted character array is ");
          for (int i = 0; i < arr.Length; ++i)
              Console.Write(arr[i]);
      }
  }
  // This code is contributed by Sam007.
• PHP
  <?php
  // PHP Program for counting sort
  $RANGE = 255;
  // The main function that sort
  // the given string arr[] in
  // alphabatical order
  function countSort($arr)
  {
      global $RANGE;
      // The output character array
      // that will have sorted arr
      $output = array(strlen($arr));
      $len = strlen($arr);
      // Create a count array to
      // store count of inidividul
      // characters and initialize
      // count array as 0
      $count = array_fill(0, $RANGE + 1, 0);
      // Store count of
      // each character
      for($i = 0; $i < $len; ++$i)
          ++$count[ord($arr[$i])];
      // Change count[i] so that
      // count[i] now contains
      // actual position of this
      // character in output array
      for ($i = 1; $i <= $RANGE; ++$i)
          $count[$i] += $count[$i - 1];
      // Build the output
      // character array
      // To make it stable we are operating
      // in reverse order.
      for ($i = $len-1; $i >= 0 ; $i--)
      {
          $output[$count[ord($arr[$i])] - 1] = $arr[$i];
          --$count[ord($arr[$i])];
      }
      // Copy the output array to
      // arr, so that arr now
      // contains sorted characters
      for ($i = 0; $i < $len; ++$i)
          $arr[$i] = $output[$i];
  return $arr;
  }
  // Driver Code
  $arr = "geeksforgeeks"; //"applepp";
  $arr = countSort($arr);
  echo "Sorted character array is " . $arr;
  // This code is contributed by mits
  ?>
• Javascript
  Javas<script>
  // Javascript implementation of Counting Sort
  function sort(arr)
  {
      var n = arr.length;
      // The output character array that will have sorted arr
      var output = Array.from({length: n}, (_, i) => 0);
      // Create a count array to store count of inidividul
      // characters and initialize count array as 0
      var count = Array.from({length: 256}, (_, i) => 0);
      // store count of each character
      for (var i = 0; i < n; ++i)
          ++count[arr[i].charCodeAt(0)];
      // Change count[i] so that count[i] now contains actual
      // position of this character in output array
      for (var i = 1; i <= 255; ++i)
          count[i] += count[i - 1];
      // Build the output character array
      // To make it stable we are operating in reverse order.
      for (var i = n - 1; i >= 0; i--) {
          output[count[arr[i].charCodeAt(0)] - 1] = arr[i];
          --count[arr[i].charCodeAt(0)];
      }
      // Copy the output array to arr, so that arr now
      // contains sorted characters
      for (var i = 0; i < n; ++i)
          arr[i] = output[i];
       return arr;
  }
  // Driver method
      var arr = [ 'g', 'e', 'e', 'k', 's', 'f', 'o',
                     'r', 'g', 'e', 'e', 'k', 's' ];
      arr = sort(arr);
      document.write("Sorted character array is ");
      for (var i = 0; i < arr.length; ++i)
          document.write(arr[i]);
  // This code is contributed by shikhasingrajput
  </script>
  cript

Output:
Sorted character array is eeeefggkkorss

Time Complexity: O(n+k) where n is the number of elements in input array and k is the range of input. 

Auxiliary Space: O(n+k)
The problem with the previous counting sort was that we could not sort the elements if we have negative numbers in it. Because there are no negative array indices. So what we do is, we find the minimum element and we will store count of that minimum element at zero index.

• C++
  // Counting sort which takes negative numbers as well
  #include <algorithm>
  #include <iostream>
  #include <vector>
  using namespace std;
  void countSort(vector<int>& arr)
  {
      int max = *max_element(arr.begin(), arr.end());
      int min = *min_element(arr.begin(), arr.end());
      int range = max - min + 1;
      vector<int> count(range), output(arr.size());
      for (int i = 0; i < arr.size(); i++)
          count[arr[i] - min]++;
      for (int i = 1; i < count.size(); i++)
          count[i] += count[i - 1];
      for (int i = arr.size() - 1; i >= 0; i--) {
          output[count[arr[i] - min] - 1] = arr[i];
          count[arr[i] - min]--;
      }
      for (int i = 0; i < arr.size(); i++)
          arr[i] = output[i];
  }
  void printArray(vector<int>& arr)
  {
      for (int i = 0; i < arr.size(); i++)
          cout << arr[i] << " ";
      cout << "\n";
  }
  int main()
  {
      vector<int> arr = { -5, -10, 0, -3, 8, 5, -1, 10 };
      countSort(arr);
      printArray(arr);
      return 0;
  }
• Java
  // Counting sort which takes negative numbers as well
  import java.util.*;
  class GFG {
      static void countSort(int[] arr)
      {
          int max = Arrays.stream(arr).max().getAsInt();
          int min = Arrays.stream(arr).min().getAsInt();
          int range = max - min + 1;
          int count[] = new int[range];
          int output[] = new int[arr.length];
          for (int i = 0; i < arr.length; i++) {
              count[arr[i] - min]++;
          }
          for (int i = 1; i < count.length; i++) {
              count[i] += count[i - 1];
          }
          for (int i = arr.length - 1; i >= 0; i--) {
              output[count[arr[i] - min] - 1] = arr[i];
              count[arr[i] - min]--;
          }
          for (int i = 0; i < arr.length; i++) {
              arr[i] = output[i];
          }
      }
      static void printArray(int[] arr)
      {
          for (int i = 0; i < arr.length; i++) {
              System.out.print(arr[i] + " ");
          }
          System.out.println("");
      }
       // Driver code
      public static void main(String[] args)
      {
          int[] arr = { -5, -10, 0, -3, 8, 5, -1, 10 };
          countSort(arr);
          printArray(arr);
      }
  }
  // This code is contributed by princiRaj1992
• Python3
  # Python program for counting sort
  # which takes negative numbers as well
  # The function that sorts the given arr[]
  def count_sort(arr):
      max_element = int(max(arr))
      min_element = int(min(arr))
      range_of_elements = max_element - min_element + 1
      # Create a count array to store count of individual
      # elements and initialize count array as 0
      count_arr = [0 for _ in range(range_of_elements)]
      output_arr = [0 for _ in range(len(arr))]
      # Store count of each character
      for i in range(0, len(arr)):
          count_arr[arr[i]-min_element] += 1
      # Change count_arr[i] so that count_arr[i] now contains actual
      # position of this element in output array
      for i in range(1, len(count_arr)):
          count_arr[i] += count_arr[i-1]
      # Build the output character array
      for i in range(len(arr)-1, -1, -1):
          output_arr[count_arr[arr[i] - min_element] - 1] = arr[i]
          count_arr[arr[i] - min_element] -= 1
      # Copy the output array to arr, so that arr now
      # contains sorted characters
      for i in range(0, len(arr)):
          arr[i] = output_arr[i]
      return arr
  # Driver program to test above function
  arr = [-5, -10, 0, -3, 8, 5, -1, 10]
  ans = count_sort(arr)
  print("Sorted character array is " + str(ans))
• C#
  // Counting sort which takes negative numbers as well
  using System;
  using System.Collections.Generic;
  using System.Linq;
  class GFG
  {
    static void countSort(int[] arr)
    {
      int max = arr.Max();
      int min = arr.Min();
      int range = max - min + 1;
      int []count = new int[range];
      int []output = new int[arr.Length];
      for (int i = 0; i < arr.Length; i++) {
        count[arr[i] - min]++;
      }
      for (int i = 1; i < count.Length; i++) {
        count[i] += count[i - 1];
      }
      for (int i = arr.Length - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
      }
      for (int i = 0; i < arr.Length; i++) {
        arr[i] = output[i];
      }
    }
    static void printArray(int[] arr)
    {
      for (int i = 0; i < arr.Length; i++)
      {
        Console.Write(arr[i] + " ");
      }
      Console.WriteLine("");
    }
     // Driver code
    public static void Main(string[] args)
    {
      int[] arr = { -5, -10, 0, -3, 8, 5, -1, 10 };
      countSort(arr);
      printArray(arr);
    }
  }
  // This code is contributed by rutvik_56.
• Javascript
  <script>
  // Counting sort which takes negative numbers as well
      function countSort(arr)
      {
      var max = Math.max.apply(Math, arr);
      var min = Math.min.apply(Math, arr);
      var range = max - min + 1;
      var count = Array.from({length: range}, (_, i) => 0);
      var output = Array.from({length: arr.length}, (_, i) => 0);
      for (i = 0; i < arr.length; i++) {
          count[arr[i] - min]++;
      }
      for (i = 1; i < count.length; i++) {
          count[i] += count[i - 1];
      }
      for (i = arr.length - 1; i >= 0; i--) {
          output[count[arr[i] - min] - 1] = arr[i];
          count[arr[i] - min]--;
      }
      for (i = 0; i < arr.length; i++) {
          arr[i] = output[i];
      }
  }
  function printArray(arr)
  {
      for (i = 0; i < arr.length; i++)
      {
          document.write(arr[i] + " ");
      }
  document.write('<br>');
  }
  // Driver code
  var arr = [ -5, -10, 0, -3, 8, 5, -1, 10 ];
  countSort(arr);
  printArray(arr);
  // This code is contributed by Amit Katiyar
  </script>

Output:
-10 -5 -3 -1 0 5 8 10 

Points to be noted:

1. Counting sort is efficient if the range of input data is not significantly greater than the number of objects to be sorted. Consider the situation where the input sequence is between range 1 to 10K and the data is 10, 5, 10K, 5K.
2. It is not a comparison based sorting. It running time complexity is O(n) with space proportional to the range of data.
3. It is often used as a sub-routine to another sorting algorithm like radix sort.
4. Counting sort uses a partial hashing to count the occurrence of the data object in O(1).
5. Counting sort can be extended to work for negative inputs also.

Exercise: 

1. Modify above code to sort the input data in the range from M to N.
2. Is counting sort stable and online?
3. Thoughts on parallelizing the counting sort algorithm.

Snapshots: