Sorting Algorithms- 6 | Algorithms - Computer Science Engineering (CSE) PDF Download

Radix Sort

The lower bound for Comparison based sorting algorithm (Merge Sort, Heap Sort, Quick-Sort .. etc) is Ω(nLogn), i.e., they cannot do better than nLogn.
Counting sort is a linear time sorting algorithm that sort in O(n+k) time when elements are in the range from 1 to k.

What if the elements are in the range from 1 to n²?
We can’t use counting sort because counting sort will take O(n2) which is worse than comparison-based sorting algorithms. Can we sort such an array in linear time?
Radix Sort is the answer. The idea of Radix Sort is to do digit by digit sort starting from least significant digit to most significant digit. Radix sort uses counting sort as a subroutine to sort.

The Radix Sort Algorithm

1. Do following for each digit i where i varies from least significant digit to the most significant digit.

• Sort input array using counting sort (or any stable sort) according to the i’th digit.

Example:
Original, unsorted list:
170, 45, 75, 90, 802, 24, 2, 66
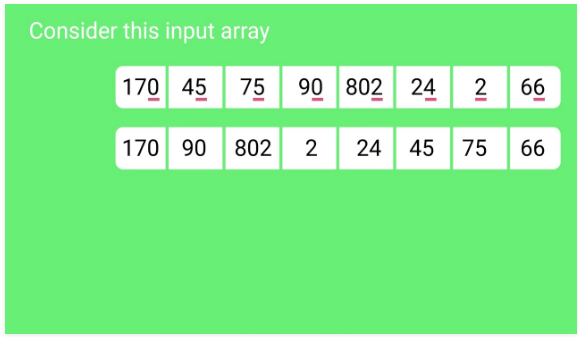
Sorting by least significant digit (1s place) gives:
[*Notice that we keep 802 before 2, because 802 occurred
before 2 in the original list, and similarly for pairs
170 & 90 and 45 & 75.]
170, 90, 802, 2, 24, 45, 75, 66
Sorting by next digit (10s place) gives:
[*Notice that 802 again comes before 2 as 802 comes before
2 in the previous list.]
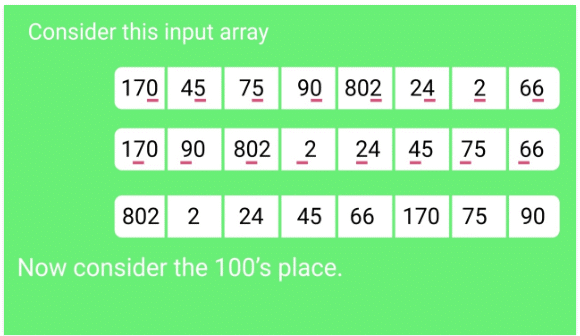
802, 2, 24, 45, 66, 170, 75, 90
Sorting by the most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802

What is the running time of Radix Sort? 

Let there be d digits in input integers. Radix Sort takes O(d*(n+b)) time where b is the base for representing numbers, for example, for the decimal system, b is 10. What is the value of d? If k is the maximum possible value, then d would be O(log_b(k)). So overall time complexity is O((n+b) * log_b(k)). Which looks more than the time complexity of comparison-based sorting algorithms for a large k. Let us first limit k. Let k <= nc where c is a constant. In that case, the complexity becomes O(nLog_b(n)). But it still doesn’t beat comparison-based sorting algorithms. 

What if we make the value of b larger?. What should be the value of b to make the time complexity linear? If we set b as n, we get the time complexity as O(n). In other words, we can sort an array of integers with a range from 1 to n^c if the numbers are represented in base n (or every digit takes log₂(n) bits).

Is Radix Sort preferable to Comparison based sorting algorithms like Quick-Sort?
If we have log₂n bits for every digit, the running time of Radix appears to be better than Quick Sort for a wide range of input numbers. The constant factors hidden in asymptotic notation are higher for Radix Sort and Quick-Sort uses hardware caches more effectively. Also, Radix sort uses counting sort as a subroutine and counting sort takes extra space to sort numbers.

Implementation of Radix Sort
Following is a simple implementation of Radix Sort. For simplicity, the value of d is assumed to be 10. We recommend you to see Counting Sort for details of countSort() function in below code.

• C++
  // C++ implementation of Radix Sort
  #include <iostream>
  using namespace std;
  // A utility function to get maximum value in arr[]
  int getMax(int arr[], int n)
  {
      int mx = arr[0];
      for (int i = 1; i < n; i++)
          if (arr[i] > mx)
              mx = arr[i];
      return mx;
  }
  // A function to do counting sort of arr[] according to
  // the digit represented by exp.
  void countSort(int arr[], int n, int exp)
  {
      int output[n]; // output array
      int i, count[10] = { 0 };
      // Store count of occurrences in count[]
      for (i = 0; i < n; i++)
          count[(arr[i] / exp) % 10]++;
      // Change count[i] so that count[i] now contains actual
      //  position of this digit in output[]
      for (i = 1; i < 10; i++)
          count[i] += count[i - 1];
      // Build the output array
      for (i = n - 1; i >= 0; i--) {
          output[count[(arr[i] / exp) % 10] - 1] = arr[i];
          count[(arr[i] / exp) % 10]--;
      }
      // Copy the output array to arr[], so that arr[] now
      // contains sorted numbers according to current digit
      for (i = 0; i < n; i++)
          arr[i] = output[i];
  }
  // The main function to that sorts arr[] of size n using
  // Radix Sort
  void radixsort(int arr[], int n)
  {
      // Find the maximum number to know number of digits
      int m = getMax(arr, n);
      // Do counting sort for every digit. Note that instead
      // of passing digit number, exp is passed. exp is 10^i
      // where i is current digit number
      for (int exp = 1; m / exp > 0; exp *= 10)
          countSort(arr, n, exp);
  }
  // A utility function to print an array
  void print(int arr[], int n)
  {
      for (int i = 0; i < n; i++)
          cout << arr[i] << " ";
  }
  // Driver Code
  int main()
  {
      int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
      int n = sizeof(arr) / sizeof(arr[0]);
        // Function Call
        radixsort(arr, n);
      print(arr, n);
      return 0;
  }
• Java
  // Radix sort Java implementation
  import java.io.*;
  import java.util.*;
  class Radix {
      // A utility function to get maximum value in arr[]
      static int getMax(int arr[], int n)
      {
          int mx = arr[0];
          for (int i = 1; i < n; i++)
              if (arr[i] > mx)
                  mx = arr[i];
          return mx;
      }
      // A function to do counting sort of arr[] according to
      // the digit represented by exp.
      static void countSort(int arr[], int n, int exp)
      {
          int output[] = new int[n]; // output array
          int i;
          int count[] = new int[10];
          Arrays.fill(count, 0);
          // Store count of occurrences in count[]
          for (i = 0; i < n; i++)
              count[(arr[i] / exp) % 10]++;
          // Change count[i] so that count[i] now contains
          // actual position of this digit in output[]
          for (i = 1; i < 10; i++)
              count[i] += count[i - 1];
          // Build the output array
          for (i = n - 1; i >= 0; i--) {
              output[count[(arr[i] / exp) % 10] - 1] = arr[i];
              count[(arr[i] / exp) % 10]--;
          }
          // Copy the output array to arr[], so that arr[] now
          // contains sorted numbers according to current digit
          for (i = 0; i < n; i++)
              arr[i] = output[i];
      }
      // The main function to that sorts arr[] of size n using
      // Radix Sort
      static void radixsort(int arr[], int n)
      {
          // Find the maximum number to know number of digits
          int m = getMax(arr, n);
         // Do counting sort for every digit. Note that
          // instead of passing digit number, exp is passed.
         // exp is 10^i where i is current digit number
          for (int exp = 1; m / exp > 0; exp *= 10)
              countSort(arr, n, exp);
      }
      // A utility function to print an array
      static void print(int arr[], int n)
      {
          for (int i = 0; i < n; i++)
              System.out.print(arr[i] + " ");
      }
      /*Driver Code*/
      public static void main(String[] args)
      {
          int arr[] = { 170, 45, 75, 90, 802, 24, 2, 66 };
          int n = arr.length;
            // Function Call
          radixsort(arr, n);
          print(arr, n);
      }
  }
  /* This code is contributed by Devesh Agrawal */
• Python
  # Python program for implementation of Radix Sort
  # A function to do counting sort of arr[] according to
  # the digit represented by exp.
  def countingSort(arr, exp1):
      n = len(arr)
      # The output array elements that will have sorted arr
      output = [0] * (n)
      # initialize count array as 0
      count = [0] * (10)
      # Store count of occurrences in count[]
      for i in range(0, n):
          index = (arr[i] / exp1)
          count[int(index % 10)] += 1
      # Change count[i] so that count[i] now contains actual
      # position of this digit in output array
      for i in range(1, 10):
          count[i] += count[i - 1]
      # Build the output array
      i = n - 1
      while i >= 0:
          index = (arr[i] / exp1)
          output[count[int(index % 10)] - 1] = arr[i]
          count[int(index % 10)] -= 1
          i -= 1
      # Copying the output array to arr[],
      # so that arr now contains sorted numbers
      i = 0
      for i in range(0, len(arr)):
          arr[i] = output[i]
  # Method to do Radix Sort
  def radixSort(arr):
      # Find the maximum number to know number of digits
      max1 = max(arr)
      # Do counting sort for every digit. Note that instead
      # of passing digit number, exp is passed. exp is 10^i
      # where i is current digit number
      exp = 1
      while max1 / exp > 0:
          countingSort(arr, exp)
          exp *= 10
  # Driver code
  arr = [170, 45, 75, 90, 802, 24, 2, 66]
  # Function Call
  radixSort(arr)
  for i in range(len(arr)):
      print(arr[i])
  # This code is contributed by Mohit Kumra
  # Edited by Patrick Gallagher
• C#
  // C# implementation of Radix Sort
  using System;
  class GFG {
      public static int getMax(int[] arr, int n)
      {
          int mx = arr[0];
          for (int i = 1; i < n; i++)
              if (arr[i] > mx)
                  mx = arr[i];
          return mx;
      }
      // A function to do counting sort of arr[] according to
      // the digit represented by exp.
      public static void countSort(int[] arr, int n, int exp)
      {
          int[] output = new int[n]; // output array
          int i;
          int[] count = new int[10];
          // initializing all elements of count to 0
          for (i = 0; i < 10; i++)
              count[i] = 0;
          // Store count of occurrences in count[]
          for (i = 0; i < n; i++)
              count[(arr[i] / exp) % 10]++;
          // Change count[i] so that count[i] now contains
          // actual
          //  position of this digit in output[]
          for (i = 1; i < 10; i++)
              count[i] += count[i - 1];
          // Build the output array
          for (i = n - 1; i >= 0; i--) {
              output[count[(arr[i] / exp) % 10] - 1] = arr[i];
              count[(arr[i] / exp) % 10]--;
          }
          // Copy the output array to arr[], so that arr[] now
          // contains sorted numbers according to current
          // digit
          for (i = 0; i < n; i++)
              arr[i] = output[i];
      }
      // The main function to that sorts arr[] of size n using
      // Radix Sort
      public static void radixsort(int[] arr, int n)
      {
          // Find the maximum number to know number of digits
          int m = getMax(arr, n);
          // Do counting sort for every digit. Note that
          // instead of passing digit number, exp is passed.
          // exp is 10^i where i is current digit number
          for (int exp = 1; m / exp > 0; exp *= 10)
              countSort(arr, n, exp);
      }
      // A utility function to print an array
      public static void print(int[] arr, int n)
      {
          for (int i = 0; i < n; i++)
              Console.Write(arr[i] + " ");
      }
      // Driver Code
      public static void Main()
      {
          int[] arr = { 170, 45, 75, 90, 802, 24, 2, 66 };
          int n = arr.Length;
          // Function Call
          radixsort(arr, n);
          print(arr, n);
      }
      // This code is contributed by DrRoot_
  }
• PHP
  <?php
  // PHP implementation of Radix Sort
  // A function to do counting sort of arr[]
  // according to the digit represented by exp.
  function countSort(&$arr, $n, $exp)
  {
      $output = array_fill(0, $n, 0); // output array
      $count = array_fill(0, 10, 0);
      // Store count of occurrences in count[]
      for ($i = 0; $i < $n; $i++)
          $count[ ($arr[$i] / $exp) % 10 ]++;
      // Change count[i] so that count[i]
      // now contains actual position of
      // this digit in output[]
      for ($i = 1; $i < 10; $i++)
          $count[$i] += $count[$i - 1];
      // Build the output array
      for ($i = $n - 1; $i >= 0; $i--)
      {
          $output[$count[ ($arr[$i] /
                           $exp) % 10 ] - 1] = $arr[$i];
          $count[ ($arr[$i] / $exp) % 10 ]--;
      }
      // Copy the output array to arr[], so
      // that arr[] now contains sorted numbers
      // according to current digit
      for ($i = 0; $i < $n; $i++)
          $arr[$i] = $output[$i];
  }
  // The main function to that sorts arr[]
  // of size n using Radix Sort
  function radixsort(&$arr, $n)
  {
      // Find the maximum number to know
      // number of digits
      $m = max($arr);
      // Do counting sort for every digit. Note
      // that instead of passing digit number,
      // exp is passed. exp is 10^i where i is
      // current digit number
      for ($exp = 1; $m / $exp > 0; $exp *= 10)
          countSort($arr, $n, $exp);
  }
  // A utility function to print an array
  function PrintArray(&$arr,$n)
  {
      for ($i = 0; $i < $n; $i++)
          echo $arr[$i] . " ";
  }
  // Driver Code
  $arr = array(170, 45, 75, 90, 802, 24, 2, 66);
  $n = count($arr);
  // Function Call
  radixsort($arr, $n);
  PrintArray($arr, $n);
  // This code is contributed by rathbhupendra
  ?>

Output
2 24 45 66 75 90 170 802
Following is the another way of the implementation of the radix sort while using bucket sort technique, it might not look simple while having a look at code but if you give  a shot it’s quite easy, to know more about the bucket sort and understand the logic behind the technique.

• C++
  // implementation of radix sort using bin/bucket sort
  #include <bits/stdc++.h>
  using namespace std;
  // structure for a single linked list to help further in the
  // sorting
  struct node {
      int data;
      node* next;
  };
  // function for creating a new node in the linked list
  struct node* create(int x)
  {
      node* temp = new node();
      temp->data = x;
      temp->next = NULL;
      return temp;
  }
  // utility function to append node in the linked list
  // here head is passed by reference, to know more about this
  // search pass by reference
  void insert(node*& head, int n)
  {
      if (head == NULL) {
          head = create(n);
          return;
      }
      node* t = head;
      while (t->next != NULL)
          t = t->next;
      t->next = create(n);
  }
  // utility function to pop an element from front in the list
  // for the sake of stability in sorting
  int del(node*& head)
  {
      if (head == NULL)
          return 0;
      node* temp = head;
      // storing the value of head before updating
      int val = head->data;
      // updation of head to next node
      head = head->next;
      delete temp;
      return val;
  }
  // utility function to get the number of digits in the
  // max_element
  int digits(int n)
  {
      int i = 1;
      if (n < 10)
          return 1;
      while (n > (int)pow(10, i))
          i++;
      return i;
  }
  void radix_sort(vector<int>& arr)
  {
      // size of the array to be sorted
      int sz = arr.size();
      // getting the maximum element in the array
      int max_val = *max_element(arr.begin(), arr.end());
      // getting digits in the maximum element
      int d = digits(max_val);
      // creating buckets to store the pointers
      node** bins;
      // array of pointers to linked list of size 10 as
      // integers are decimal numbers so they can hold numbers
      // from 0-9 only, that's why size of 10
      bins = new node*[10];
      // intializing the hash array with null to all
      for (int i = 0; i < 10; i++)
          bins[i] = NULL;
      // first loop working for a constan time only and inner
      // loop is iterating through the array to store elements
      // of array in the linked list by their digits value
      for (int i = 0; i < d; i++) {
          for (int j = 0; j < sz; j++) // bins updation
              insert(bins[(arr[j] / (int)pow(10, i)) % 10],
                     arr[j]);
          int x = 0, y = 0;
          // write back to the array after each pass
          while (x < 10) {
              while (bins[x] != NULL)
                  arr[y++] = del(bins[x]);
              x++;
          }
      }
  }
  // a utility function to print the sorted array
  void print(vector<int> arr)
  {
      for (int i = 0; i < arr.size(); i++)
          cout << arr[i] << " ";
      cout << endl;
  }
  int main()
  {
      vector<int> arr = { 573, 25, 415, 12, 161, 6 };
      // function call
      radix_sort(arr);
      print(arr);
      return 0;
  }

Output
6 12 25 161 415 573
Time complexities remains same as in the first method, it’s just the implementation through another method.

Snapshots: