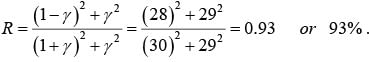Applications of Electromagnetic Waves | Electricity & Magnetism - Physics PDF Download
Reflection and Refraction at Dielectric Interface
Normal Incidence
Suppose xy plane forms the boundary between two linear media. A plane wave of frequency ω , traveling in the z-direction and polarized in the x direction, approaches the interface from the left then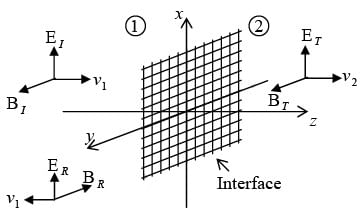
Incident Wave 
Reflected Wave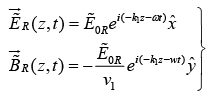
Transmitted Wave
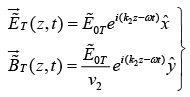
At z = 0 , the combined field on the left 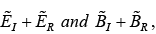 must join the fields on the right
must join the fields on the right 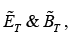 in accordance with the boundary conditions
in accordance with the boundary conditions
(i) 
(ii) 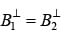
(iii) 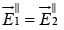
(iv) 
In this case there are no electric component perpendicular to the surface, so (i) & (ii) are trivial. However (iii) gives
While (iv) gives,
where
Solving above two equations we get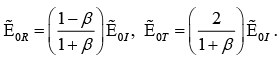
if 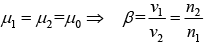 (For non-magnetic medium)
(For non-magnetic medium)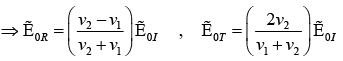
Note: Reflected wave is in phase if v2 >v1 or n2< n1 and out of phase if v2 <v1 or n2> n1.
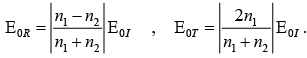
Since Intensity 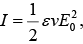 then the ratio of the reflected intensity to the incident intensity is the Reflection coefficient
then the ratio of the reflected intensity to the incident intensity is the Reflection coefficient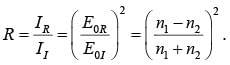
The ratio of the transmitted intensity to the incident intensity is the Transmission coefficient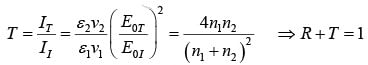
Example 1: Calculate the reflection coefficient for light at an air-to-dielectric interface
(μ1 =μ2= μ0 , n1 =1,n2 = 1.5) at optical frequencyω = 4×1015 s−1.
Reflection coefficient
Thus only 4% of light is reflected and 96% is transmitted.
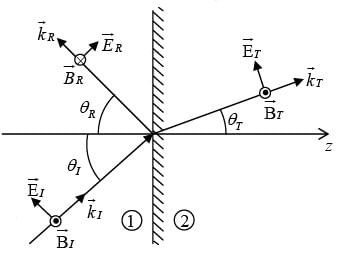
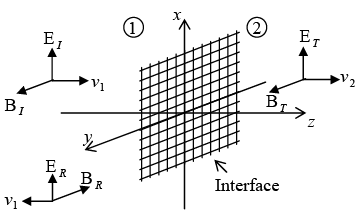
Oblique Incidence
In oblique incidence an incoming wave meets the boundary at an arbitrary angle θI . Of course, normal incidence is really just a special case of oblique incidence with θI = 0 . Suppose that a monochromatic plane wave of frequency ω , approaches the interface from the left then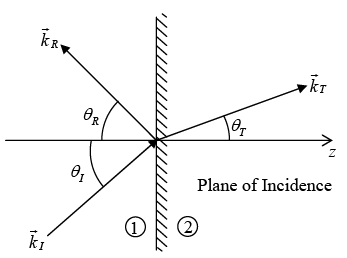
Incident Wave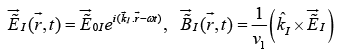
Reflected Wave
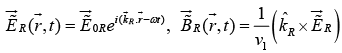
Transmitted Wave
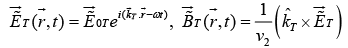
All three waves have the same frequencyω . The three wave numbers are related by (ω = kv ) as
The combined field in medium (1), 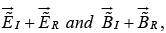 must join the fields
must join the fields 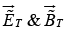 in medium (2), using the boundary conditions.
in medium (2), using the boundary conditions.
(i) 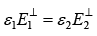
(ii) 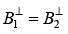
(iii) 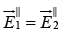
(iv) 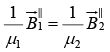
First Law (Plane of Incidence)
The incident, reflected and transmitted wave vectors form a plane (called the plane of incidence), which also includes normal to the surface.
Second law (Law of Reflection)
The angle of incidence is equal to the angle of reflection i.e.
θI= θR
Third Law: (Law of Refraction, or Snell’s law)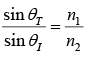
Fresnel’s Relation (Parallel and Perpendicular Polarization) Case-I: (Polarization in the Plane of Incidence) Applying Boundary conditions, we get Reflected and transmitted amplitudes
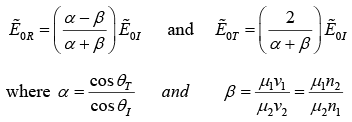
These are known as Fresnel’s equations.
Notice that transmitted wave is always in phase with the incident one; the reflected wave is either in phase, if α > β , or 1800 out phase if α < β .
The amplitudes of the transmitted and reflected waves depend on the angle of incidence, because α is a function of θI :
Brewster’s Angle
At Brewster’s angle (θB ) reflected light is completely extinguished whenα = β , or
For non-magnetic medium and hence
and hence
Thus at Brewster angle  reflected and transmitted rays are perpendicular to each other.
reflected and transmitted rays are perpendicular to each other.
Critical Angle
When light enters from denser to rarer medium ( n1 > n2 ) then after a critical angle (θC ) there is total internal reflection.
Reflection and Transmission Coefficient
The power per unit are striking the interface is 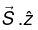 Thus the incident intensity is
Thus the incident intensity is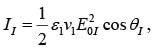
while reflected and transmitted intensities are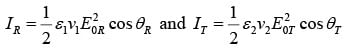
Reflection coefficient
Transmission coefficient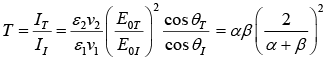
⇒ R+T = 1
Case-II: (Polarization Perpendicular to plane of Incidence)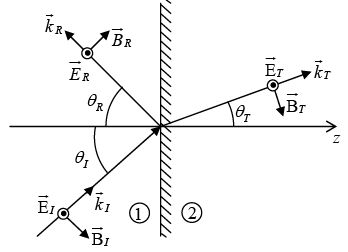
Applying Boundary conditions, we get Reflected and transmitted amplitudes
In this case Brewster’s angle (θB ) is not possible i.e reflected light is never completely extinguished (since αβ = 1 is not possible).
Reflection and Transmission coefficient
The power per unit are striking the interface is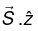 . Thus the incident intensity is
. Thus the incident intensity is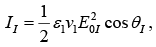
while reflected and transmitted intensities are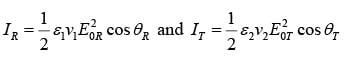
Reflection coefficient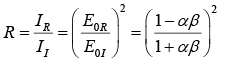
Transmission coefficient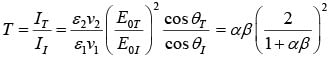
⇒ R+T = 1
Reflection at Conducting Surface (Normal Incidence)
Suppose xy plane forms the boundary between a non-conducting linear medium (1) and a conductor (2). A plane wave of frequencyω , traveling in the z-direction and polarized in the x direction, approaches the interface from the left then
Incident Wave
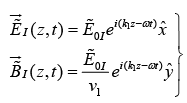
Reflected Wave
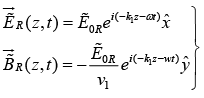
Transmitted Wave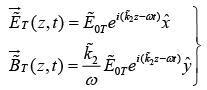
where 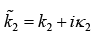 where k2 and κ2 are real and imaginary part of
where k2 and κ2 are real and imaginary part of 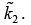
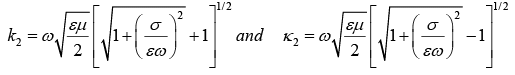
At z = 0 , the combined field on the left 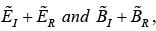 must join the fields on the right
must join the fields on the right 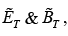 in accordance with the boundary conditions
in accordance with the boundary conditions
(i) 
(ii) 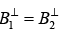
(iii) 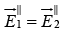
(iv) 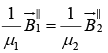
In this case there are no electric component perpendicular to the surface, so (i) & (ii) are trivial.
However (iii) gives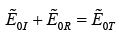
While (iv) gives,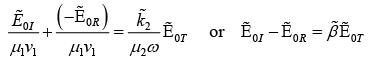
where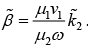
Solving above two equations we get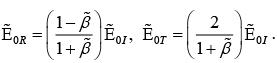
Note:
(i) For a perfect conductor 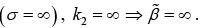 Thus
Thus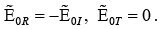
In this case wave is totally reflected, with a 1800 phase shift.
(ii) For good conductor
Reflection Coefficient
Example 2: Calculate the reflection coefficient for light at an air-to-silver interface μ1=μ2= μ0 , ε1 = ε0, σ = 6 ×107 Ω−1 m− at optical frequency ω = 4×1015 s−1 .
Reflection coefficient
Thus 93% of light is reflected and only 7% is transmitted.
|
82 videos|32 docs|22 tests
|
FAQs on Applications of Electromagnetic Waves - Electricity & Magnetism - Physics
| 1. What are some common applications of electromagnetic waves? |  |
| 2. How are electromagnetic waves used in wireless communication? |  |
| 3. How do electromagnetic waves contribute to medical imaging? |  |
| 4. How are electromagnetic waves used in remote sensing? |  |
| 5. How do electromagnetic waves contribute to radar systems? |  |