Elementary Ideas about Dia-, Para- & Ferromagnetism | Solid State Physics, Devices & Electronics PDF Download
Elementary Ideas about Dia-, Para- and Ferromagnetism
Materials which look permanent magnetic dipole are called diamagnetic if there are permanent magnetic dipoles associated with the atoms in a material such a material may be paramagnetic ferromagnetic, anti-ferromagnetic, depending on the interaction between the individual dipoles. Thus if the interaction between the atomic permanent dipole moment is zero (or negligible), a material will be paramagnetic. If the dipoles interact in such a manner that they tend to line up in parallel, the material will be ferromagnetic, if the neighbouring dipoles tend to line up so that they are anti-parallel the material is anti-ferromagnetic or ferromagnetic, depending on the magnitudes of the dipoles on the two “sub lattice” as indicated schematically for a one-dimensional model in figure shows:
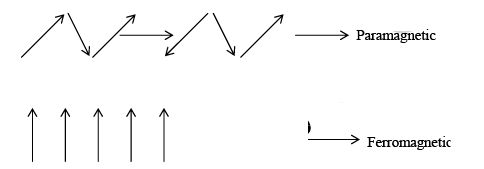
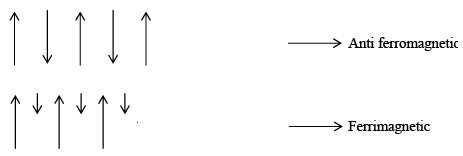
In case of antiferromagnetic configuration that net magnetic moment is zero, because the spins of neigbhouring dipoles are equal and opposite whereas in ferrimagnetic the spins of neighbouring dipoles are opposite and unequal in magnitude, thus in this case there may be relatively large net magnetization.
The magnetic materials can also be classified on the basis of the behaviour when these materials are placed in a magnetic field.
➤ Magnetic Properties
There are two fields to consider:
The magnetic field 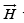 which is generated by currents according to Ampere’s law.
which is generated by currents according to Ampere’s law.
 is measured in Am−1 (Oersteds in old units)
is measured in Am−1 (Oersteds in old units)
The magnetic induction, or magnetic flux density, 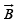 which gives the energy of a dipole in a field,
which gives the energy of a dipole in a field, 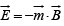 and the torque experienced by a dipole moment
and the torque experienced by a dipole moment 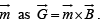
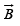 is measured in Wb m−2 or T (Gauss in old units).
is measured in Wb m−2 or T (Gauss in old units).
In free space, 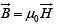
In a meterial 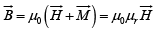
where μr is the relative permeability, χ is the magnetic susceptibility, which is a dimensionless quantity
Note, through that χ is sometimes tabulated as the molar susceptibility χm = Vmχ
where Vm is the volume occupted by one mole, or as the mass susceptibility 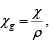 where ρ is the density.
where ρ is the density.
M , the magnetisation, is the dipole moment per unit volume.
M = χ H
In general μr (and hence χ ) will depend on position and will be tensors (so that B is not necessarily parrallel to H )
Diamagnetism
Classically, we have Lenz’s law, which states that the action of a magnetic field on the orbital motion of an electron causes a back-emf which opposes the magnetic field which causes it.
Frankly, this is an unsatisfactory explanation, but we cannot do better until we have studied the inclusion of magnetic fields into quantum mechanics using magnetic vector potentials.
Imagine an electron in an atom as a charge e moving clockwise in the x-y plane in a circle of radius a , area A , with angular velocity ω .
This is equivalent to a current I = charge/time=eω / ( 2π ) ,
so there is a magnetic moment μ = IA= eωa2/2
The electron is kept in this orbit by a central force F =meω2a
Now if a flux density B is applied in the z - direction there will be a Lorentz force giving an additional force along a radius
ΔF = evB= eωaB
If we assume the charge keeps moving in a circle of the same radius it will have a new angular velocity ω ′ ,
meω′2a = F− ΔF so meω'2a = meω2a-eωaB, or ω'2 = ω2 = -(eωB/me)
If there change in frequency is small we have ω ′2 −ω2 ≈ 2ωΔω where Δω= ω′ −ω.
Thus 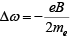 where eB/2m0 is called the Larmor frequency.
where eB/2m0 is called the Larmor frequency.
Substituting back into μ = IA= eωa2/2,
we find a change in magnetic moment 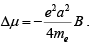
Recall that a was the radius of a ring of current perpendicular to the field: if we average over a spherical atom 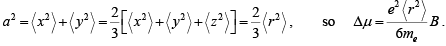
If we have n atoms per volume, each with p electrons in the outer shells, the magnetisation will be 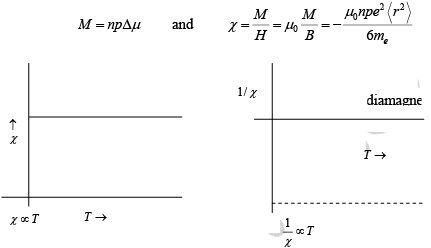
Range: −1≤ χ ≤0 ≈ −10−5 ( −ve)
Note: χ = 0 only for vacuum.
Diamagnetic susceptibility:
- Negative
- Typically −10−6 to− 10−5
- Independent of temperature
- Always present, even when there are no permanent dipole moments on the atoms.
Paramagnetism
Paramagnetism occurs when the material contains permanent magnetic moments. If the magnetic moments do not interact with each other, they will be randomly arranged in the absence of a magnetic field.
When a field is applied, there is a balance between the internal energy trying to arrange the moments parallel to the field and entropy trying to randomize them.
The magnetic moments arise from electrons, but if we they are localized at atomic sites we can regard them as distinguishable, and use Boltzmann statistics.
➤ Paramagnetism of spin -1/2 ions:
The spin is either up or down relative to the field, and so the magnetic moment is either +μB or −μB , where μB = 
The corresponding energies in a flux density B are −μBB and μBB, so the average magnetic moment per atom is 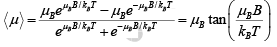
For small z , tanh z ≈z, so for small fields or high temperature 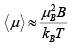
If there are n atoms per volume, then, 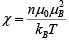
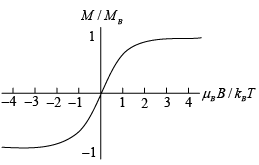
Clearly, though, for low T or large B the magnetic moment per atom saturates, as it must, as the largest magnetization possible saturation magnetization has all the spins aligned fully, MB = nμB
➤ Genral J ionic paramagnetism
An atomic angular momentum J made of spin S and orbital angular momentum quantum number L , will have a magnetic moment gJμBJ , where gJ is the Lande g - factor 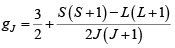
The average atomic magnetic moment will be 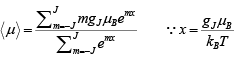
If we assume that T is large and / or B is small, we can expand the exponential, giving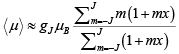
Note that 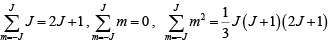
Then 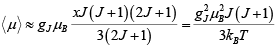
This leads to susceptibility 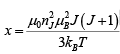
This is curie’s Law, often written X = C/T where C is curie’s constant. 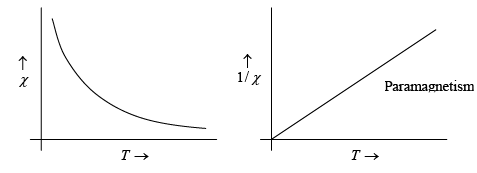
Ferromagnetism
Ferromagnetic materials are spontaneously magnetized even in the absence of external magnetic field. All ferromagnetic material becomes paramagnetic above a temperature called Curie temperature Tc ; Ferromagnetic is the property of materials to be strongly attracted to a magnetic field and to become a powerful magnet. The source of ferromagnetism namely.
- Electrons given ferromagnetism must originate from partly filled shells in the free atoms, in order that the energy bands formed from these shells have vacant quantum state available for occupation when the electrons align their spins.
- The density of state must be high so that the increase in kinetic energy due to the promotion of electrons when these align their spins, shall be smaller than the decrease in energy due to the exchange interaction.
For ferromagnetics the Curie temperature TC and the constant θ in the Curie-Weiss law are nearly identical. A small difference exists, however, because the transition from ferromagnetism to paramagnetism is gradual.
The most important ferromagnetic materials are Fe, CO, Ni, Gd the ferromagnetic properties of the transition elements Fe, CO and Ni are due to the spins of the inner unpaired electrons. In Fe,CO and Ni the unpaired inner 3d electrons are responsible for the ferromagnetism the spins of the 3d electrons of adjacent atoms align in a parallel direction by a phenomenon called spontaneous magnetization Ms. The parallel alignment of atomic magnetic domains. The parallel alignment of the magnetic dipoles of atoms of Fe,CO and Ni is due to the creator energy known as exchange interaction.
Using Heitler-London theory of chemical bonding, it can be shown that the total energy of a system of two atoms contains an exchange energy term given by Vij − 2 JeSiSj.
Where Si and Si represent the spins of the two atoms and Je is the exchange integral which is assumed to be the same for any pair of atoms.
Consider the Curie temperature; for T >Tc the spontaneous magnetization is zero and an external field will be have to be applied to produce some magnetization. This field should, however, be weak enough to avoid the saturation state. In such a state, we find equation 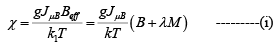
while 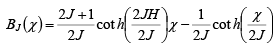
and Beff = B + BE = B + λ M where M = NgJμBBJ(χ) ----------(ii)
for that χ << 1, 
Therefore, the expression (ii) become (1) M = NgμB(J+1)X/3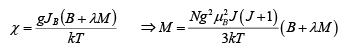
which gives 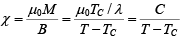
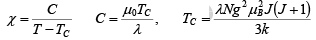
This expression is known as curie-weiss law. It is satisfactory explain the susceptibility and temperature dependence in paramagnetic region. 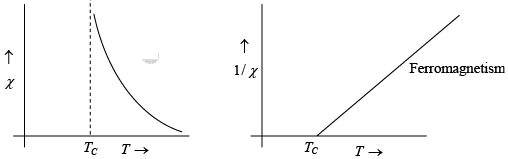
Range χ >> 1 ≈ very large and + ve .
|
91 videos|21 docs|25 tests
|
FAQs on Elementary Ideas about Dia-, Para- & Ferromagnetism - Solid State Physics, Devices & Electronics
| 1. What is dia-, para-, and ferromagnetism? |  |
| 2. How do diamagnetic materials behave in a magnetic field? |  |
| 3. What are examples of paramagnetic materials? |  |
| 4. Explain the behavior of ferromagnetic materials in a magnetic field. |  |
| 5. How can ferromagnetic materials be magnetized? |  |
|
91 videos|21 docs|25 tests
|

|
Explore Courses for Physics exam
|

|

















