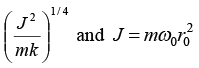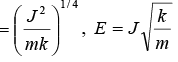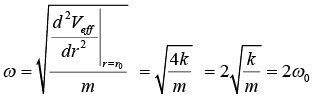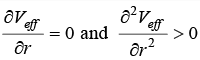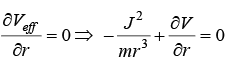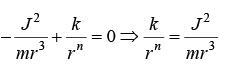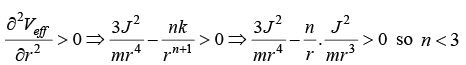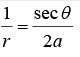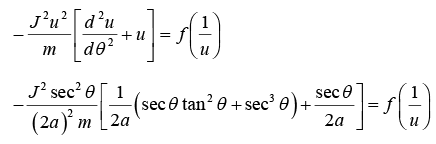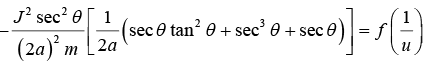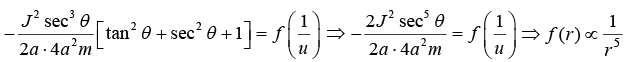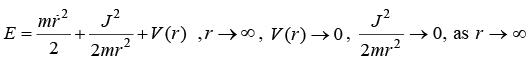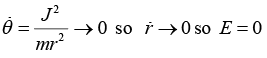Central Force | Mechanics & General Properties of Matter - Physics PDF Download
Central Force
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center.
In central force potential V is only function of r, a central force is always a conservative force; the magnitude F of a central force can always be expressed as the derivative of a time independent potential energy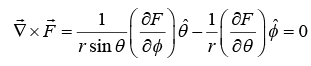
And the force F is defined as F = 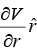 (force is only in radial direction)
(force is only in radial direction)
External torque and angular momentum of system
but for central force, 
External torque τ = 0 , so angular momentum 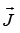 is conserved.
is conserved.
Now, if we calculate 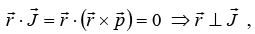 hence position vector
hence position vector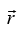 is perpendicular to angular momentum vector
is perpendicular to angular momentum vector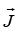 , hence
, hence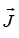 is conserved. Its magnitude and direction both are fixed, The central force
is conserved. Its magnitude and direction both are fixed, The central force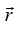 is along to r and can exert no torque on the mass m. Hence the angular momentum J of m is constant. However, J is fixed in space, and it follows that r can only move in the plane perpendicular to J through the origin.
is along to r and can exert no torque on the mass m. Hence the angular momentum J of m is constant. However, J is fixed in space, and it follows that r can only move in the plane perpendicular to J through the origin.
Equation of Motion for central force
The equation of motion in polar coordinate is given by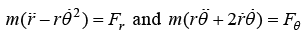
For central force problem F(r) = - ∂V/∂r and Fθ = 0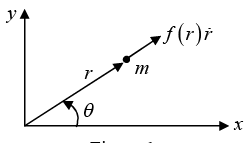
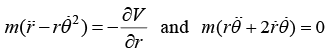
Equation of Motion and Condition for Circular Orbit Condition of circular orbit From equation of motion in radial part m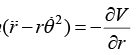
For circular orbit of radius r0, r = r0 and 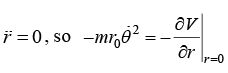
And 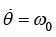 is identified as angular frequency in circular orbit.
is identified as angular frequency in circular orbit.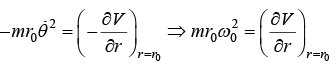
For circular orbit angular frequency ω0 is given by ω0 =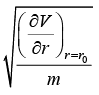
Conservation of Angular Momentum and Areal Velocity
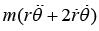 = F0, but for central force, Fθ = 0 ⇒
= F0, but for central force, Fθ = 0 ⇒ 
Angular momentum =  it is also seen
it is also seen
So motion due to central force is confine into a plane and angular momentum  is perpendicular to that plane.
is perpendicular to that plane.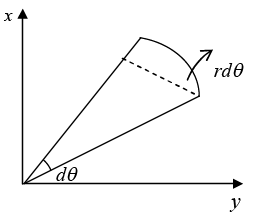 For the central force problem, now A = 1/2 r.rdθ
For the central force problem, now A = 1/2 r.rdθ
Areal velocity = 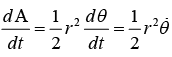
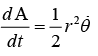 . It is given that
. It is given that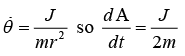
Which means equal area will swept in equal time
Total Energy of the System
Hence total energy is not explicitly function of time t so ∂E/∂r = 0. One can conclude that total energy in central potential is constant.
E = 1/2 mv2 + V(r) and Velocity 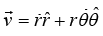
So total energy, E = 1/2 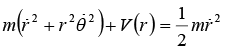
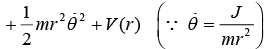
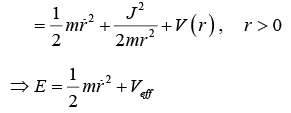
The sum rotational kinetic energy 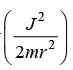 as a function of only r and potential energy as a function of only r i.e. V(r) are identified as effective potential
as a function of only r and potential energy as a function of only r i.e. V(r) are identified as effective potential 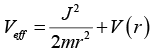
The concept of effective potential allow to two dimensional system in one system as Veffective is only function of r .
Analysis of effective potential
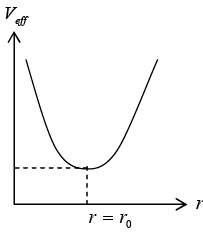
The effective potential is define as 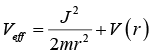 The nature of orbit will dependent on nature of effective potential and total energy of a system which is shown in figure.
The nature of orbit will dependent on nature of effective potential and total energy of a system which is shown in figure.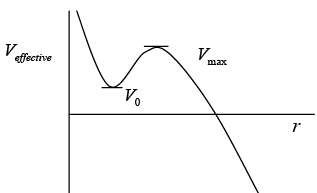 And lets discuss how variation of energy will leads to shape of orbit
And lets discuss how variation of energy will leads to shape of orbit
Case 1: if energy E < V0 there is turning point at r = a the classical region as r > a , the particle is unbounded so nature of orbit may be either parabolic or hyperbolic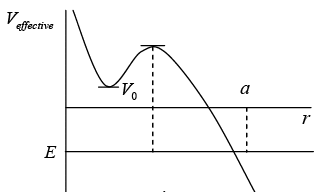
Case 2: If energy E = V0 there r = r0 is identified as stable equilibrium point because 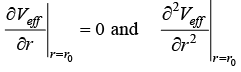 > 0 so possible orbit is Veffective circular in nature with radius r0 for region, the angular frequency in circular orbit is ω0 =
> 0 so possible orbit is Veffective circular in nature with radius r0 for region, the angular frequency in circular orbit is ω0 = 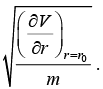
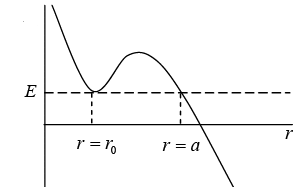 There is turning point at r = a. r > a is also identified as classical region. The particle is unbounded so nature of orbit may be either parabolic or hyperbolic
There is turning point at r = a. r > a is also identified as classical region. The particle is unbounded so nature of orbit may be either parabolic or hyperbolic
Case 3: If energy V0 < E < Vmax the particle is bounded between turning point a and b and shape of orbit is elliptical in region.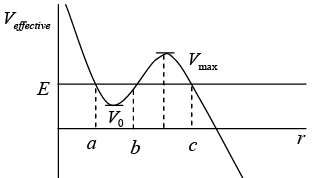 Radius r = r0 of circular orbit is also identified as stable equilibrium point, so
Radius r = r0 of circular orbit is also identified as stable equilibrium point, so 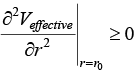 . Then new orbit is identified as elliptical orbit. The angular frequency in new elliptical orbit is identified as oscillatory motion so for small oscillation the angular frequency is
. Then new orbit is identified as elliptical orbit. The angular frequency in new elliptical orbit is identified as oscillatory motion so for small oscillation the angular frequency is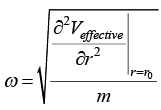 Another turning point is r = c , region r > c is identified as classical region the particle is unbounded so nature of orbit may be either parabolic or hyperbolic.
Another turning point is r = c , region r > c is identified as classical region the particle is unbounded so nature of orbit may be either parabolic or hyperbolic.
Case 4: E = Vmax hence r = b is unstable equilibrium point. , the orbit can be unstable circular of radius b .there is another possible shape as it is elliptical between turning point a and unstable equilibrium point b .unbounded orbit is also possible for r > b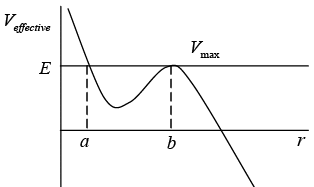 Case 5: E > Vmax there is only one turning point r = a and region r > a is identified as classical region the particle is unbounded so nature of orbit may be either parabolic or hyperbolic
Case 5: E > Vmax there is only one turning point r = a and region r > a is identified as classical region the particle is unbounded so nature of orbit may be either parabolic or hyperbolic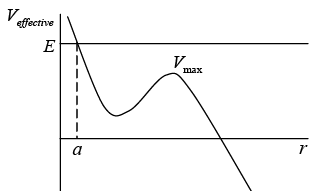
Differential Equation of Orbit
From equation of motion in radial part, 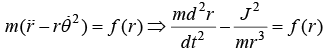
where J = mr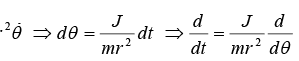
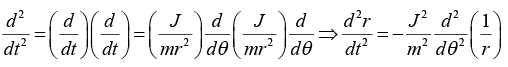
Example 1: Consider that the motion of a particle of mass m in the potential field V(r) = kr2/2 If l is angular momentum,
(a) What is effective potential (Veff) of the system. plot Veff vs r
(b) Find value of energy such that motion is circular in nature.
(c) If particle is slightly disturbed from circular orbit such that its angular remain constant. What will nature of new orbit? Find the angular frequency of new orbit in term of m, l, k.
(a)
(b)+ kr = 0 at r = r0 so r0 =
For circular motion, mω02r0 = kr0, where r0 is radius of circle ω0 =
Total energy, E =
(c) orbit is elliptical in nature
Example 2: A particle of mass m moves under the influence of an attractive central force f (r).
(a) What is condition that orbit is circular in nature if J is the angular momentum of particle
(b) If force is in form of f(r) = -k/rn determine the maximum value of n for which the circular orbit can be stable.
(a) if veff
, for circular stable orbit
(b) f(r) = -k/rn, for circular motion
It is given ∂V/∂r = - f(r) if f(r) = -k/rn ⇒ ∂V/∂r = k/rn
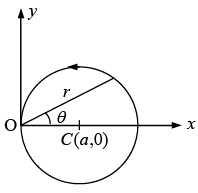
Example 3: A particle of mass m and angular momentum l is moving under the action of a central force f(r) along a circular path of radius a as shown in the figure. The force centre O lies on the orbit.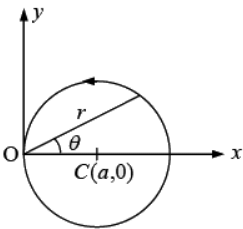 (a) Given the orbit equation in a central field motion.
(a) Given the orbit equation in a central field motion.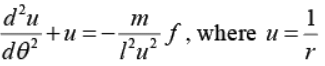
Determine the form of force in terms of l ,m, a and r.
(b) Calculate the total energy of the particle assuming that the potential energy V(r) ⇢ 0 as r⇢ ∞.
(a) from the figure, 2cosθ,
(b)
Hence,
|
61 videos|23 docs|25 tests
|
FAQs on Central Force - Mechanics & General Properties of Matter - Physics
| 1. What is a central force? |  |
| 2. What are some examples of central forces? |  |
| 3. How is a central force different from a non-central force? |  |
| 4. What is the significance of central forces in physics? |  |
| 5. How are central forces related to the IIT JAM exam? |  |