Velocity & Acceleration in Simple Harmonic Motion | Physics for JAMB PDF Download
Acceleration in SHM
We know what acceleration is. It is velocity per unit time. We can calculate the acceleration of a particle performing S.H.M. Lets learn how. The differential equation of linear S.H.M. is d2x/dt2 + (k/m)x = 0 where d2x/dt2 is the acceleration of the particle, x is the displacement of the particle, m is the mass of the particle and k is the force constant. We know that k/m = ω2 where ω is the angular frequency.
Therefore, d2x/dt2 +ω2 x = 0
Hence, acceleration of S.H.M. = d2x/dt2 = – ω2 x (I)
The negative sign indicated that acceleration and displacement are in opposite direction of each other. Equation I is the expression of acceleration of S.H.M. Practically, the motion of a particle performing S.H.M. is accelerated because its velocity keeps changing either by a constant number or varied number.
Take a simple pendulum for example. When we swing a pendulum, it moves to and fro about its mean position. But after some time, it eventually stops and returns to its mean position. This type of simple harmonic motion in which velocity or amplitude keeps changing is damped simple harmonic motion.
Velocity in SHM
Velocity is distance per unit time. We can obtain the expression for velocity using the expression for acceleration.Let’s see how. Acceleration d2x/dt2 = dv/dt = dv/dx × dx/dt. But dx/dt = velocity ‘v’
Therefore, acceleration = v(dv/dx) (II)
When we substitute equation II in equation I, we get, v(dv/dx) = – ω2 x.
∴ vdv = – ω2 xdx
After integrating both sides, we get,
∫vdv = ∫-ω2 xdx = -ω2∫ xdx
Hence, v2 /2 = -ω2 x2 /2 + C where C is the constant of integration. Now, to find the vaue of C, lets consider boundary value condition. When a particle performing SHM is at the extreme position, displacement of the particle is maximum and velocity is zero. (a is the amplitude of SHM)
Therefore, At x = ± a, v = 0
And 0 = – ω2 a2 /2 + C
Hence, C = ω2 a2 /2
Let’s substitute this value of C in equation v2 /2 = -ω2 x2 /2 + C
∴ v2 /2 = -ω2 x2 /2 + ω2 a2 /2
∴ v2 = ω2 (a2 – x2 )
Taking square root on both sides, we get,
v = ± ω √(a2 – x2 ) (III)
Equation III is the expression of the velocity of S.H.M. The double sign indicates that when a particle passes through a given point in the positive direction of x, v is positive, and when it passes through the same point in opposite direction of x, v is negative.
Maximum and Minimum velocity
We know the velocity of a particle performing S.H.M. is given by, v = ± ω √a2 – x2. At mean position, x = 0. Therefore, v = ± ω √a2 – 02 = ± ω √a2 = ± aω. Therefore, at mean position, velocity of the particle performing S.H.M. is maximum which is Vmax = ± aω. At extreme position, x = ±a
Therefore, v = ± ω √a2 – a2 = ω × 0 = 0 . Therefore, at extreme position, velocity of the particle performing S.H.M. is minimum which is Vmin = 0 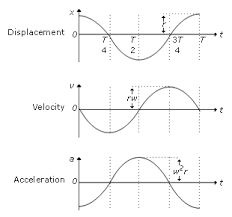
Solved Examples
Q: What is the value of acceleration at the mean position?
Solution: At mean position, x =0
∴ acceleration = -ω2 x = -ω2 × 0 = 0. Therefore, the value of acceleration at the mean position is minimum and it is zero.
|
260 videos|253 docs|230 tests
|
















