Force Law for Simple Harmonic Motion | Physics for JAMB PDF Download
Periodic Motion
We already know what periodic motion is. A motion which repeats itself in equal intervals of time is periodic motion. For example, the motion of the hands of a clock, the motion of the wheels of a car and the motion of a merry-go-round. All these motions are repetitive in nature. They repeat themselves in a fixed amount of time.
Oscillatory Motion
An oscillatory motion is a periodic motion in which an object moves to and fro about its equilibrium position. The object performs the same set of movements again and again after a fixed time. One such set of movements is an Oscillation. The motion of a simple pendulum, the motion of leaves vibrating in a breeze and the motion of a cradle are all examples of oscillatory motion.
Simple Harmonic Motion (S.H.M.)
Simple harmonic motion is the simplest example of oscillatory motion. When an object moves to and fro along a straight line, it performs the simple harmonic motion. All examples of oscillatory motion are the examples of simple harmonic motion.
When we swing a simple pendulum, it moves away from its mean equilibrium position. After it reaches its extreme position, where it has maximum displacement, it stops, that is, its velocity becomes zero. It returns to its equilibrium position due to a force which acts in towards the equilibrium position.
Now, it passes through its mean position but doesn’t stop. It moves towards its other extreme position. After which, it again returns to its equilibrium position. One such complete motion is known as an Oscillation. The motion of a simple pendulum is a great example of simple harmonic motion.
Force Law For Simple Harmonic Motion
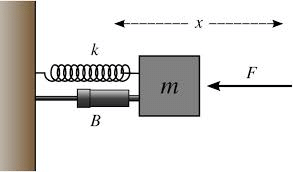
Let’s derive the force law for simple harmonic motion with an example. A spring-block system is the simplest example of simple harmonic motion. Consider a block of mass m attached to a spring, which in turn is fixed to a rigid wall. The block rests on a frictionless surface. When we do not pull the spring, that is, no force is applied on it, it is in its equilibrium position. In this state, the net force acting on it is zero. Now, let’s perform two actions and observe what happens.
- When we pull the block outwards, there is a force acting on the block that tries to pull it inwards, that is, towards its equilibrium position.
- When we push the block inwards, there is a force acting on the block tries to push it outwards, that is, towards its equilibrium position.
In both the cases, we can see that there is a force acting on the block that tries to return the block to its equilibrium position. This force is the restoring force and the force law for simple harmonic motion is based on this force. Let’s learn how to calculate this law.
Derivation of Force Law for Simple Harmonic Motion
Let the restoring force be F and the displacement of the block from its equilibrium position be x. Therefore, from the cases we observed, we can say that the restoring force is directly proportional to the displacement from the mean position.
∴ F = – kx (I)
where k is a constant known as the force constant.Its unit is N/m in S.I. system and dynes/cm in C.G.S. system. The negative sign indicates that the restoring force and the displacement are always in opposite direction. The equation I is the simplest form of force law for simple harmonic motion. It proves the basic rule of simple harmonic motion, that is, force and displacement should be in opposite direction.
Further, we know that F = ma. Therefore, a = F/m. Substituting this value in Equation I, we get,
a = – kx/m = – ω2x (where k/m = ω2) (II)
Hence, Equations I and II are the forms of force law of simple harmonic motion. Note that the restoring force is always towards the mean position and in the opposite direction of that of displacement.
Solved Examples
Q: A hydrogen atom has mass 1.68×10−27 kg. When attached to a certain massive molecule it oscillates with a frequency 1014 Hz and with an amplitude 10−9 cm. Find the force acting on the hydrogen atom.
(a) 2.21×10-9 N
(b) 3.31×10-9 N
(c) 4.42×10-9 N
(d) 6.63×10-9 N
Ans: (d)
Solution: We know that F = kx. Let’s first find the value of k. We know that ω2 = (k/m); where the letters have their usual meaning. Also, we know that ω = 2πν, therefore ω2 = (2πν)2 = (k/m).
Therefore, k = 4π2ν2m. Hence, F = k x = 4π2ν2m x
Therefore, F = 6.63 × 10-9 N
|
260 videos|253 docs|230 tests
|
FAQs on Force Law for Simple Harmonic Motion - Physics for JAMB
| 1. What is periodic motion? |  |
| 2. What is simple harmonic motion? |  |
| 3. What is the force law for simple harmonic motion? |  |
| 4. How is simple harmonic motion different from other types of periodic motion? |  |
| 5. What are some real-life examples of simple harmonic motion? |  |





















