Energy in Simple Harmonic Motion | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Energy in Simple Harmonic Motion
The total energy that a particle possesses while performing simple harmonic motion is energy in simple harmonic motion. Take a pendulum for example. When it is at its mean position, it is at rest. When it moves towards its extreme position, it is in motion and as soon as it reaches its extreme position, it comes to rest again. Therefore, in order to calculate the energy in simple harmonic motion, we need to calculate the kinetic and potential energy that the particle possesses.
Kinetic Energy (K.E.) in S.H.M
Kinetic energy is the energy possessed by an object when it is in motion. Let’s learn how to calculate the kinetic energy of an object. Consider a particle with mass m performing simple harmonic motion along a path AB. Let O be its mean position. Therefore, OA = OB = a.
The instantaneous velocity of the particle performing S.H.M. at a distance x from the mean position is given by
v= ±ω √a2 – x2
∴ v2 = ω2 ( a2 – x2)
∴ Kinetic energy= 1/2 mv2 = 1/2 m ω2 ( a2 – x2)
As, k/m = ω2
∴ k = m ω2
Kinetic energy= 1/2 k ( a2 – x2) . The equations Ia and Ib can both be used for calculating the kinetic energy of the particle.
Potential Energy(P.E.) of Particle Performing S.H.M.
Potential energy is the energy possessed by the particle when it is at rest. Let’s learn how to calculate the potential energy of a particle performing S.H.M. Consider a particle of mass m performing simple harmonic motion at a distance x from its mean position. You know the restoring force acting on the particle is F= -kx where k is the force constant.
Now, the particle is given further infinitesimal displacement dx against the restoring force F. Let the work done to displace the particle be dw. Therefore, The work done dw during the displacement is
dw = – fdx = – (- kx)dx = kxdx
Therefore, the total work done to displace the particle now from 0 to x is
∫dw= ∫kxdx = k ∫x dx
Hence Total work done = 1/2 K x2 = 1/2 m ω2x2
The total work done here is stored in the form of potential energy.
Therefore Potential energy = 1/2 kx2 = 1/2 m ω2x2
Equations IIa and IIb are equations of potential energy of the particle. Thus, potential energy is directly proportional to the square of the displacement, that is P.E. α x2.
Total Energy in Simple Harmonic Motion (T.E.)
The total energy in simple harmonic motion is the sum of its potential energy and kinetic energy.
Thus, T.E. = K.E. + P.E. = 1/2 k ( a2 – x2) + 1/2 K x2 = 1/2 k a2
Hence, T.E.= E = 1/2 m ω2a2
Equation III is the equation of total energy in a simple harmonic motion of a particle performing the simple harmonic motion. As ω2 , a2 are constants, the total energy in the simple harmonic motion of a particle performing simple harmonic motion remains constant. Therefore, it is independent of displacement x.
As ω= 2πf , E= 1/2 m ( 2πf )2a2
∴ E= 2mπ2f 2a2
As 2 and π2 constants, we have T.E. ∼ m, T.E. ∼ f 2, and T.E. ∼ a2
Thus, the total energy in the simple harmonic motion of a particle is:
- Directly proportional to its mass
- Directly proportional to the square of the frequency of oscillations and
- Directly proportional to the square of the amplitude of oscillation.
The law of conservation of energy states that energy can neither be created nor destroyed. Therefore, the total energy in simple harmonic motion will always be constant. However, kinetic energy and potential energy are interchangeable. Given below is the graph of kinetic and potential energy vs instantaneous displacement.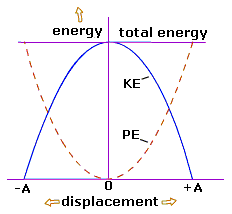
In the graph, we can see that,
- At the mean position, the total energy in simple harmonic motion is purely kinetic and at the extreme position, the total energy in simple harmonic motion is purely potential energy.
- At other positions, kinetic and potential energies are interconvertible and their sum is equal to 1/2 k a2.
- The nature of the graph is parabolic.
Solved Question
Q: At the mean position, the total energy in simple harmonic motion is ________
(a) purely kinetic
(b) purely potential
(c) zero
(d) None of the above
Ans: (a)
Solution: At the mean position, the velocity of the particle in S.H.M. is maximum and displacement is minimum, that is, x=0. Therefore, P.E. =1/2 K x2 = 0 and K.E. = 1/2 k ( a2 – x2) = 1/2 k ( a2 – o2) = 1/2 ka2. Thus, the total energy in simple harmonic motion is purely kinetic.
|
199 videos|422 docs|281 tests
|
FAQs on Energy in Simple Harmonic Motion - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is simple harmonic motion? |  |
| 2. How is energy related to simple harmonic motion? |  |
| 3. What is the formula for calculating the potential energy in simple harmonic motion? |  |
| 4. How does the amplitude affect the energy in simple harmonic motion? |  |
| 5. Can the energy in simple harmonic motion ever be negative? |  |

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















