Some Systems Executing Simple Harmonic Motion | Physics for JAMB PDF Download
Systems executing S.H.M.
We are going to study about two systems below that perform Simple Harmonic Motion. These systems include- a spring-block system and a simple pendulum. Let’s understand one by one how these systems perform simple harmonic motion and under what conditions.
Oscillations due to a Spring
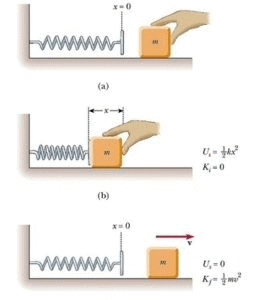
The small oscillations of a block fixed to a spring, which in turn is fixed to a wall are the simplest example of simple harmonic motion. Let the mass of the block be ‘m’. The block is placed on a frictionless horizontal surface. When we pull the block and then release it, it performs to and fro motion about its mean position. Let x=0 be the position of the block when it is at its equilibrium position. Now,
- If we pull the block outwards, there is a force exerted by the string that is directed towards the equilibrium position.
- If we push the block inwards, there is a force exerted by the string towards the equilibrium position.
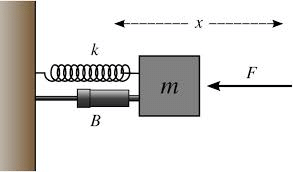
In each case, we can see that the force exerted by the spring is towards the equilibrium position. This force is called the restoring force. Let the restoring force be F and the displacement of the string from the equilibrium position be x.
Therefore, we can deduce from this system that the magnitude of restoring force exerted by a system is directly proportional to the displacement of the system from its equilibrium position. The restoring force always acts in the opposite direction of that of displacement. Therefore,
F= -kx
Here, k is the constant which is called the force constant. In this system, it is called the spring system. The value of k depends on the stiffness of the spring. A stiff spring will have larger k and a soft spring will have small k. You can see that this equation is the same as the Force law of Simple Harmonic Motion. Therefore, a spring system executes simple harmonic motion. From equation I, we have, ω= √k/m
∴ The time period (T) of the oscillator = 2π√m/k
The Simple Pendulum
A practical simple pendulum is a small heavy sphere(bob) suspended by a light and inextensible string from a rigid support. The length of the simple pendulum is the distance between the point of suspension and centre of gravity of heavy sphere.
The Simple Harmonic Motion Pendulum
The motion of Simple Pendulum as Simple Harmonic Motion When we pull a simple pendulum from its equilibrium position and then release it, it swings in a vertical plane under the influence of gravity. It begins to oscillate about its mean position. Therefore, the motion is periodic and oscillatory. Now, if we displace the pendulum by a very small angle Θ, then it performs the simple harmonic motion.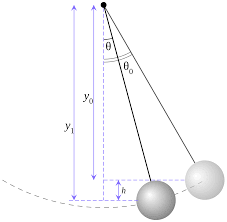
- Gravitational force, which is the weight of the bob – ‘mg’ acting in the downward direction.
- Tension T’ in the string.
Now, weight mg is resolved in two components,
- Radial component mgcosΘ along the string.
- Tangential component mgsinΘ perpendicular to the string.
Radial component mgcosΘ is balanced by Tension T’ in the string and the Tangential component mgsinΘ is the restoring force acting on mass m towards the equilibrium position. Therefore,
Restoring force, F = -mgsinΘ
The negative sign indicates that F and Θ are in opposite directions. Note that the restoring force is proportional to sinΘ instead of Θ. Therefore, it is not yet a simple harmonic motion. However, if the angle is very small, we can assume that sinΘ is nearly equal to Θ in radian. Thus, the displacement x= LΘ and for a small angle, it is nearly a straight line.
∴ Θ= x/L
Hence, assuming sinΘ= Θ, F = -mgΘ = -mgx/L. As m, g and L are constant, F α -x. For a small displacement, the restoring force is directly proportional to the displacement and its direction is opposite to that of displacement. Therefore, Simple pendulum performs linear S.H.M.
As we know, acceleration= force/mass = -mgx/L/m
∴ acceleration= -gx/L
∴ acceleration per unti displacement will be,
acceleration/x = -g/L
Also, acceleration = ω2x
∴ ω = √acceleration per unit displacement
Considering magnitude, acceleration/x = g/L = ω2
Period of a Simple Pendulum
Now, the period of a simple pendulum is, T = 2π/ω = 2π/√acceleration per unit displacement
∴ T = 2π/√g/L = 2π√L/g
The above equation is the equation of period of a simple pendulum
The frequency of Simple Pendulum
Now, frequency of a simple pendulum = f = 1/T = 1/2π√g/L. This equation is the equation of frequency of a simple pendulum.
Solved Question
Q: When does a simple pendulum perform Linear Simple Harmonic Motion?
Solution: In an ideal situation, a simple pendulum will execute periodic oscillation with constant amplitude. But in practice, the amplitude of oscillation will gradually decrease until the body comes to rest. The restoring force is proportional to sinΘ and not Θ(Θ is the angular displacement).
Therefore, this motion is not S.H.M. But for Θ as large as 10°,sinΘ can be approximated by Θ to an error in fourth decimal point. For Θ less than 6°, sinΘ ≈ Θ. Thus, for small displacement, the restoring force is directly proportional to the displacement and the pendulum performs linear S.H.M.
|
260 videos|253 docs|230 tests
|
FAQs on Some Systems Executing Simple Harmonic Motion - Physics for JAMB
| 1. What is simple harmonic motion? |  |
| 2. What are the characteristics of a system executing simple harmonic motion? |  |
| 3. How can the period of a system executing simple harmonic motion be calculated? |  |
| 4. What is the relationship between frequency and period in simple harmonic motion? |  |
| 5. Can any system exhibit simple harmonic motion? |  |
















