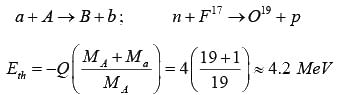Nuclear Reaction | Modern Physics PDF Download
| Table of contents |

|
| Introduction |

|
| Conservation Laws |

|
| Nuclear Reaction Kinematics (Q -Value) |

|
| Nuclear Fission |

|
| Nuclear Fusion in Stars |

|
Introduction
All the nuclear reactions are of the form
x + X → Y + y or X (x,y)Y
The equation and notation both means that particle x strikes nucleus X to produce nucleus Y and particle y. The particles x and y may be elementary particles or γ-rays or they may themselves be nuclei, eg. α -particles or deuteron. In more general nuclear equations are shown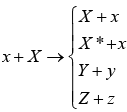
The first equation x + X → X + x represents elastic scattering in which the total K. E. of the system, projectile plus target, is the same before the collision as after. The second reaction x + X → X* + x represents inelastic scattering, in which the target nucleus X is raised into an excited state X*, and the total K.E. of the system is decreased by the amount of excited energy given to target nucleus.
The last two equations show a general nuclear equation.
Conservation Laws
In any nuclear reaction certain quantities must be conserved. The following conservation laws hold well during a nuclear reaction.
1. Conservation of Energy
2. Conservation of Linear Momentum
3. Conservation of charges
4. Conservation of Nucleons
5. Conservation of Angular Momentum
6. Conservation of Parity
7. Conservation of spin
8. Conservation of statistics
9. Conservation of Isobaric spins
The Quantities not conserved
These are magnetic dipoles moments and the electrical quadrupole moment of the reacting nuclei. These moments depends upon the internal distribution of mass, charge and current within the nuclei involved and are not subjected to conservation laws.
Nuclear Reaction Kinematics (Q -Value)
Consider the reaction
a + A → B + b
Now according to Law of conservation of energy the total energy of the reactant is equal to the total energy of the product.
(Mac2 + Ea) + (MAc2 + EA) = (MBc2 + EB) + (Mbc2 + Eb)
where Ma, MA, Mb, MB are the masses of the particles a, A, B and b respectively and Ea, EA, Eb, EB are their respective kinetic energies.
If we suppose that the target is at rest then EA = 0,
Q = EB + Eb - Ea = [(MA + Ma) - (MB + Mb)]c2
Here masses are the nuclear masses. The quantity Q is called the energy balance of the reaction or more commonly Q -value of the reaction. Thus Q is energy appearing due to disappearance of masses or mass defect in a nuclear reaction.
(i) If Q is +ve (Q > 0)
The Kinetic energy of the products is greater than that of the reactants, the reaction is then said to be exothermic or exoergic. The total mass of the reactants is greater than that of the products in this case.
(ii) If Q is -ve (Q < 0)
The reaction is said to be endothermic or endoergic, i.e. energy must be supplied usually as K. E. of the incident particles.
General solution of Q -Equation
Let the particle a strike with target A and the product nuclei B and b are observed at angle ϕ and θ to the direction of incident particle respectively.
Then applying the law of conservation of linear momentum
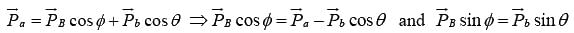
Squaring and adding above two equations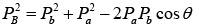 , where
, where 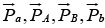 are the momenta of the particles a, A, B and b respectively.
are the momenta of the particles a, A, B and b respectively.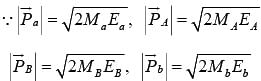
Putting these values in the equation
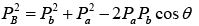
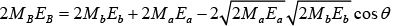
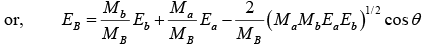
But Q = EB + Eb - Ea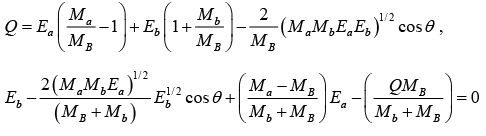
This equation is of the form x2 - 2ux- v = 0
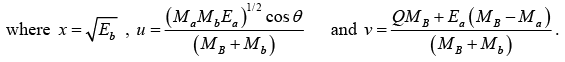
The solution of the above equation is given by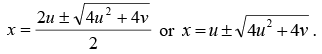
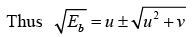
The energetically possible reactions are those for which 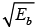 is real and +ve.
is real and +ve.
Exothermic Reaction (Q > 0)
For exothermic reaction Q > 0 and these reactions are possible even for Ea = 0
∵ Q = EB + Eb - Ea for Ea = 0 , u = 0 and 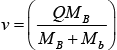
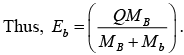
Endothermic Reaction (Q < 0)
All endothermic reactions have negative Q -Values.
When Ea →, u2 + v = -ve and hence 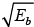 is imaginary.
is imaginary.
It means that these reactions are not possible. The smallest value of Ea at which reaction can take place is called threshold energy. The reaction first becomes possible when Ea is large enough to make
u2 + v = 0,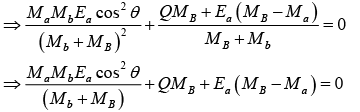
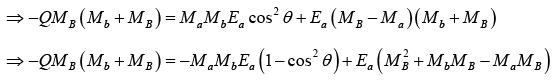
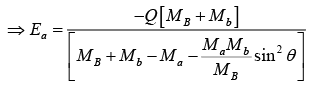
At θ = 0 , Ea is minimum and is the threshold energy Eth.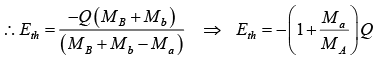
Note: Isotopic masses can be used to compute Q except in positive beta decay: (Q in mass units)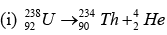
Q = [m(U)-92me)] - [m(Th)-90e + m(He) - 2me]
Q = m(U) - [m(Th) - m(He)]
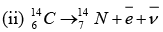
Q = m(Zn) - 30me - [m(Cu) - 29me + me]
Q = m(Zn)- [m(Cu) +2me]
Example: The Thermal Neutrons are captured by 5B10 to form 5B11 which further decays into α - particle and 3Li7. Then find the Q - value.
(Given mn = 1.008665 u, mB = 10.01611 u, mα = 4.003879 u, mLi = 7.01823 n)
5B10 + 0n1 → 5B11 → 2He4 (α) + 3Li7 + Q
Q = (MB + MN - Mα - MLi) x 931.5 MeV
Q = (10.01611 + 1.008665 - 4.003879 - 7.018231) x 931.5 ≈ 2.78 MeV ≈ 2.8 MeV
Example: Consider the nuclear reaction 7N14 x (α, p) 8O17 which occurred in Rutherford’s α-range in nitrogen experiment. The mass of N14 = 14.0031u , He4 = 4.0026 u , O17 = 16.9994u and p = 1.0078 u p. Then find the Q -value of the reaction.
a + A → B + b; α + 7N14 → 8O17 + p
Q = [(MA + Ma) - (MB + Mb)] x 931.5 MeV
Q = [14.003 + 4.0026) - (16.9994 +1.0078)] x 931.5MeV
Q = -0.0013 x 931.5MeV = -1.49 MeV
Example: A neutron beam is incident on a stationary target of fluorine atoms. The reaction F17(n,p)O19 has a Q -value of -4.0 MeV. Then find the lowest neutron energy which will make this reaction possible.
Nuclear Fission
Nuclear fission is a process in which a heavy nucleus, after capturing a neutron splits up into two lighter nuclei of comparable masses. The process is accompanied by release of a few fast neutrons and a huge amount of energy in form of K.E. of fission fragments and γ-rays.
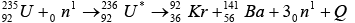
Energy released by 1 kg of Uranium
Mass of 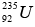 = 235.035315 u, Mass of n = 1.008665 u
= 235.035315 u, Mass of n = 1.008665 u
Total initial mass = 236.04398 u
Mass of 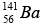 = 140.9177 u, Mass of
= 140.9177 u, Mass of 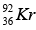 = 91.8854 u , Mass of 3n = 3.0259 u
= 91.8854 u , Mass of 3n = 3.0259 u
Total final mass = 235.8290 u
Mass defect (Δm) = initial mass- final mass = 0.21498 u
Energy released i.e Q -value = Δm x 931.5MeV ≈ 200 MeV
Number of uranium nucleus in 1 kg of uranium = 6.023 x 1023 x 1000/235
Energy released by 1 kg of uranium
= 6.023 x 1023 x 1000/235 x 200 MeV = 5.13 x 1026 MeV
Nuclear Fusion in Stars
Fusion is a process, in which the lighter nuclei fuse together and produce a heavier nucleus. The sum of the masses of the individual light nuclei is more than would be the mass of the nucleus formed by their fusion, and thus the fusion process result in liberation of energy.
Stellar energy was liberated in the formation of helium from hydrogen because large amounts of hydrogen and helium exist in the sun. Such processes are called thermonuclear reactions because energy is liberated due to very high stellar temperature. In order to interact two nuclei, that must have enough K.E. to permit them to overcome the electrostatic repulsion barrier which tends to keep them apart.
Proton-Proton Cycle
The basic energy producing process in the sun is the fusion of hydrogen nuclei into helium nuclei. This can take place in several different reaction sequences, the most common of which, the proton-proton cycle. The total evolved energy is 24.7 MeV per 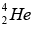 nucleus formed.
nucleus formed.
Since 24.7 MeV is 4 x 10-12 Joules , the sun’s power output of 4 x 1026 Watt means each sequence of reactions must occur 1038 times per second.
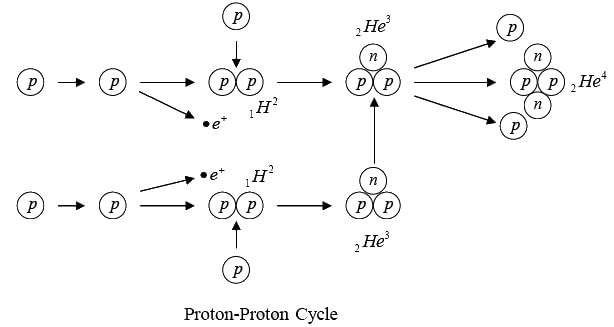
Energy is given off at each step. The net result is the combination of four hydrogen nuclei to form a helium nucleus and two positrons.
Self-sustaining fusion reactions can occur only under conditions of extreme temperature and density. The high temperature ensures that the some nuclei have the energy needed to come close enough together to interact, and the high density ensures that such collisions are frequent. A further condition for the proton-proton cycles is a large reacting mass, such as that of the sun, since much time may elapse between the initial fusion of a particular proton and its eventual incorporation in an α-particle.
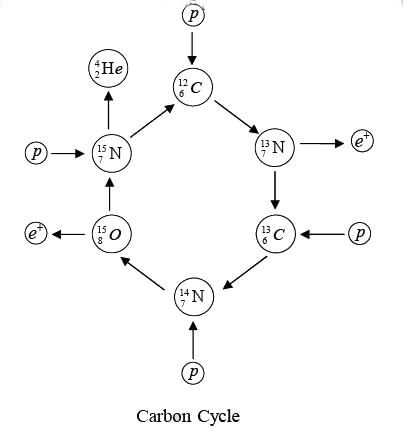
Carbon-Cycle
It also involves the combination of four hydrogen nuclei (Stars hotter than sun) to form a helium nucleus with the evolution of energy. The net result again is the formation of an α-particle and two positrons from four protons, with the evolution of 24.7 MeV. The initial 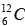 acts as a kind of catalyst for the process, since it reappears at its end.
acts as a kind of catalyst for the process, since it reappears at its end.
|
37 videos|17 docs|19 tests
|
FAQs on Nuclear Reaction - Modern Physics
| 1. What is the conservation of energy and how does it relate to nuclear reactions? |  |
| 2. What is the Q-value in nuclear reaction kinematics? |  |
| 3. What is nuclear fission and how does it occur? |  |
| 4. How does nuclear fusion occur in stars? |  |
| 5. What is the significance of nuclear reaction in the IIT JAM exam? |  |