One Dimensional System | Modern Physics PDF Download
Properties of one-dimensional motion:
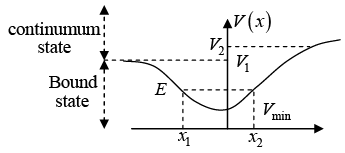
(A) Bound states (quantum mechanical discrete spectrum)
Bound states occur whenever the particle cannot move to infinity and particle is confined into limited region.
- From the figure the condition for bound states is Vmin < E < V1
- In a one dimensional potential energy, level of a bound state system are discrete and non degenerate.
- The wave function Ψn of one dimensional bound state system has n nodes i.e., Ψn vanishes n times, if n corresponds to n = 0 and n - 1 nodes, if n = 1 corresponds to the ground state.
(B) Continuous spectrum (unbound states)
Unbound states occur in those cases where the motion of the system is not confined in above figure.
- V1 < E < V2 : The energy spectrum is continuous and none of the energyeigen values is degenerate.
- E > V2 : The energy spectrum is continuous and particles motion is infinite in both directions. And this spectrum is doubly degenerate.
Current Density (J)
The probability current density is defined as,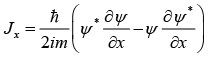
The current density can also be given as,
J = ρv
where ρ is probability density. i.e., ρ = |ψ|2 and v is velocity of particle which is ℏk/m in momentum space.
So, the current density is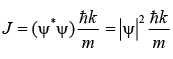
The current density and probability density will satisfy the continuity equation which is given by, 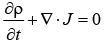
Free Particle in One Dimension
The potential of free particle is defined as, V (x) = 0; -∞ < x < ∞
The Schrödinger wave function is given by
H = Eψ
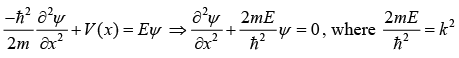
The solution is given by,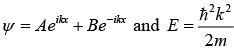
The energy eigen value of free particle is 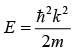 is continuous and wave function is ψ+ = Aeikx and ψ- = Ae-ikx, where ψ+ moves from positive x -axis and ψ- moves from negative x -axis.
is continuous and wave function is ψ+ = Aeikx and ψ- = Ae-ikx, where ψ+ moves from positive x -axis and ψ- moves from negative x -axis.
Hence, there are two eigenfunctions for energy, 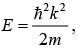 then wave function is doubly degenerate.
then wave function is doubly degenerate.
The Step Potential
If Ji is incident current density, Jr is reflection current density and Jt is transmission current density, then reflection coefficient is defined as 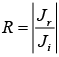 and transmission coefficient is defined as
and transmission coefficient is defined as 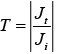
The potential step is defined as,

Case I: E > V
For x < 0 , the Schrödinger wave equation is given as
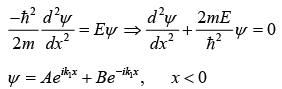
where  is incoming wave and
is incoming wave and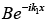 is reflected wave. In region x > 0 , where the Schrödinger wave equation is-
is reflected wave. In region x > 0 , where the Schrödinger wave equation is-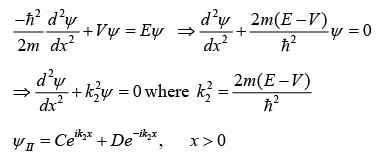
D = 0 as no wave reflected in region II i.e., x > 0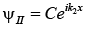 which is transmitted wave i.e.,
which is transmitted wave i.e., 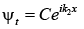
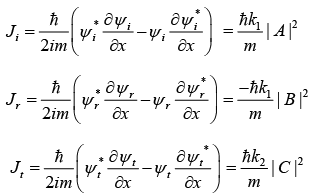
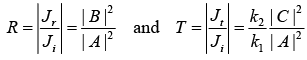
Using Boundary condition at x = 0 i.e.,
Wave must be continuous and differentiable at boundary.
So, ψ1(x = 0) = ψ2(x = 0) ⇒ A + B = C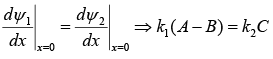
Solution of above two equations are,
Case II: E < V0 Schrodinger wave equation for x > 0
Hψ = Eψ
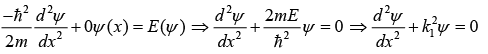
ψ = Aeikx + Beikx
If 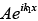 is incoming wave,
is incoming wave, 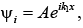 then
then 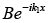 is reflected wave,
is reflected wave, 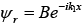
Schrödinger wave equation for x > 0
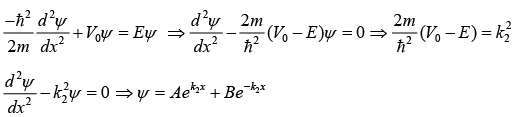
A = 0 , as wave function must vanish at x → ∞ , then 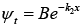
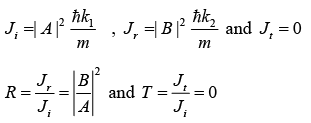
Now, we apply boundary condition at x = 0 i.e.,
ψ1 (x = 0) = ψ2 (x = 0) ⇒ (A + B) = C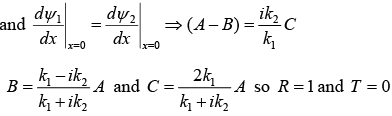
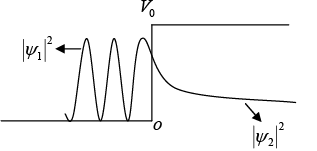
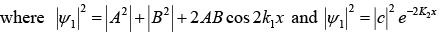
when E < V0 , there is a finite probability to find the particle at x > 0 , even if E < 0 but current density is zero in region x > 0.
Strange part of the problem is that, even if transmission coefficient is zero there is finite probability to find the particle at x > 0.
Particle in a One Dimensional Box
The potential of one dimensional box is defined as
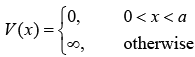
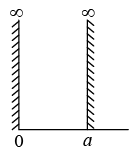
Time independent Schrödinger wave equation is given as, Hψ = Eψ for region x < 0 and x > 0 , ψ(x) = 0, because in this region potential is infinity, so probability to find the particle in that region is zero.
Schrodinger wave equation in the region, 0 < x < a
Hψ = Eψ
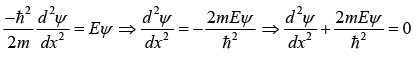
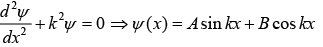
Now wave function must be continuous at the boundary
So, ψ(0) = ψ(a) = 0 ⇒ 0 = A sin0 + B cos0 = B ⇒ B = 0
Therefore, ψ(x) = A sin kx
Now, ψ(a) = 0 ⇒ A sin ka = 0 ⇒ ka = nπ, where n = 0, 1, 2, 3, ....
But for n = 0 ψ(x) = 0 so n = 0 is not possible
So, n = 1, 2, 3, .... , ka = nπ
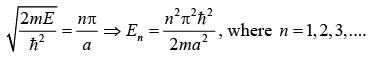
En is energy eigen value which is discrete.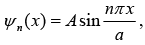 the value of A can be find with normalization condition which is
the value of A can be find with normalization condition which is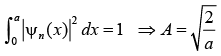
So, energy eigen function is given by 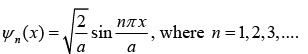
Energy eigen value is given as 
The orthonormal condition is given by
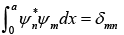
Any function f(x) can be expressed in the term of ψn (x).
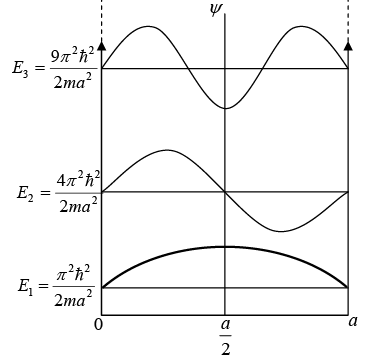
Infinite Symmetric Potential Box
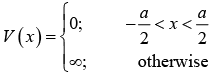
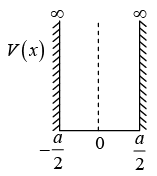
Wave function in region, 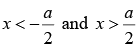 vanishes i.e., ψ(x) = 0, because potential is infinite in this region. In region,
vanishes i.e., ψ(x) = 0, because potential is infinite in this region. In region, 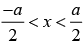 the solution of Schrödinger wave function is given by, ψ = A sin kx + B cos kx
the solution of Schrödinger wave function is given by, ψ = A sin kx + B cos kx
Parity operator will commute with Hamiltonian because wave function can have either even or odd symmetry.
Now wave function must vanish at boundary.

Solution for infinite symmetric box as mentioned above is given by
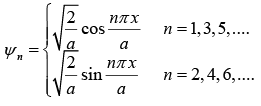
and energy eigen value,
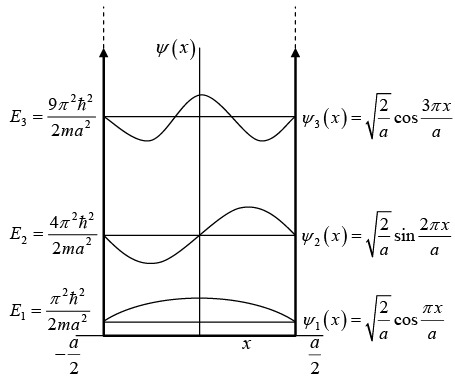 First three eigenstate are shown in the above figure.
First three eigenstate are shown in the above figure.
Square Well Finite Potential Box (graphical method)
Square well finite potential box is defined as,
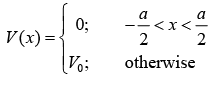
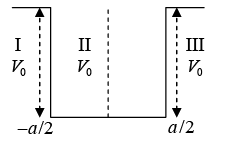
For Bound state, E < 0
Schrödinger wave solution in region I, i.e., 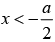
ϕ1(x) = Aeγx + Be-γx
The wave function must vanish at x → -∞ , i.e., wave function must be zero.
So, B = 0
Thus, ϕ1(x) = Aeγx ; 
Schrodinger wave solution in region II, i.e.,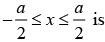
ϕI(x) = B cos kx; for even parity
ϕII(x) = B cos kx; for odd parity
(potential is symmetric about x = 0. So parity must be conserved).
Where, k2 = 2mE/ℏ2
Schrodinger wave solution in region III i.e., x > a/2
ψ = De-γx + Eeγx
The wave function must vanish at x → ∞ so E = 0



In the table below shown the number of bound states for various range of V0a2. where R denotes the radius.

Harmonic Oscillator (Parabolic potential)
The parabolic potential is defined as,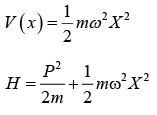
The Schrödinger wave function is given as,
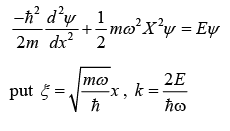

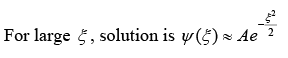
The general solution is given by 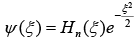
So, equation (i) reduces to 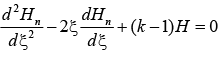
Solving series solution by putting 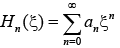
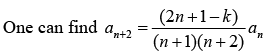
When k = 2n + 1, the equation (i) reduces to Hermite polynomial and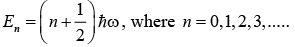
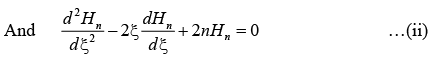
Hermite polynomials and it is given as
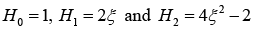
Energy eigen function is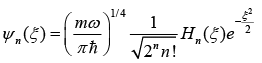
And eigen value is 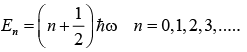
Ground state n = 0 = E = ℏω/2 is zero point energy.
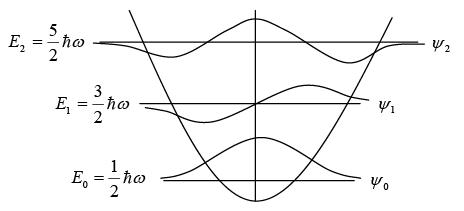
The first three stationary state and corresponding eigen value for the harmonic oscillator.
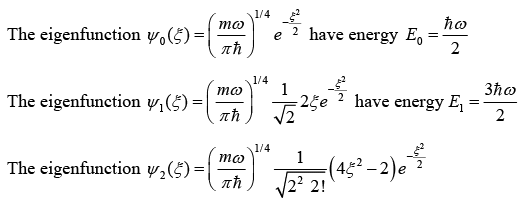
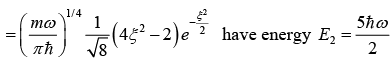
Problems on One Dimensional System:
Example: A particle of mass m is confined into a box of width L , where potential is defined as, 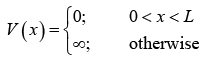
Find
(a) 〈x〉
(b) 〈x2〉
(c) 〈Px〉
(d) 〈Px2〉
(e) Δx · ΔPx
Example: A particle of mass m which moves freely inside an infinite potential well of length a has the following initial wave function.
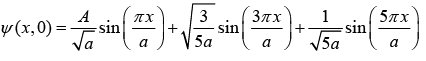
(a) Find A so that ψ(x, 0) is normalized.
(b) If measurement of energy is carried out, what are the values that will be found and what are the corresponding probability?
(c) Calculate the average energy.
Particle of mass m confine into a box of width a.
For normalized Ψ,
If energy will be measured on state |Ψ〉, the measurement of |Ψ〉, yields either
which is eigen value associated with |ϕ1〉, |ϕ3〉, |ϕ5〉 respectively.
(c) Average energy is given by 〈E〉 = ∑Ei Pi
Example: Prove for any normalized wave function of particle of mass m in one dimensional,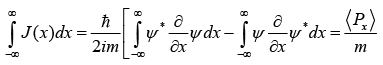
Example: Three dimensional wave function is given by, Ψ(r) = (A/r)eikr
Find the current density.
Ψ(r) = (A/r)eikr
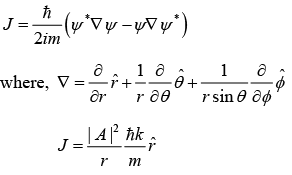
Example: A potential barrier is given as 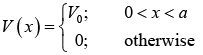
Prove that the expression of transmission probability for E < V0 is given as,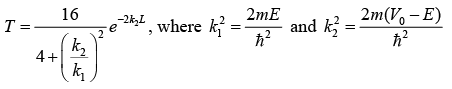
The potential is given as

Case - E < V0
The Schrödinger wave solution in region I, II and III is given by -
Boundary condition -
The transmission probability is given by
Solving the above four boundary condition
For approximation V0 > E,
Example: Consider a particle of mass m and charge q placed in uniform field,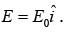 Apart from this, a restoring force corresponding to the potential V(x) = 1/2 mω2 X2 acts.
Apart from this, a restoring force corresponding to the potential V(x) = 1/2 mω2 X2 acts.
Find the lowest energy eigen value. Consider the electric field is originated at origin.
The electric potential energy at the position x will be -qEX. So the effective potential is given by
So, Hamiltonion is given by-
So, Energy is given by
Example: A particle of energy 9eV is sent towards a potential step 8eV high.
(a) What is reflection coefficient.
(b) What percentage will transmitted.
Example: A particle in the infinite square well has the initial wave function.
ψ(x, 0) = Ax(a - x); (0 ≤ x ≤ a)
(a) Find the value of A such that ψ is normalized.
(b) Write down ψ (x) in the basis of ϕn (x), where ϕn (x) is the eigen function of the nth state (wave function) for the system confined into box whose potential is given as,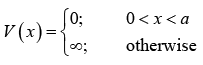
(c) Write down expression of ψ (x, t)
(a) ψ(x, 0) = Ax(a- x); 0 ≤ x ≤ a
And cn can be found with Fourier’s trick
From Schrodinger wave equation,
Example: |ϕn〉 represent the energy eigen state of a linear harmonic oscillator and if state  of harmonic state of angular frequency ω.
of harmonic state of angular frequency ω.
(a) If energy is measured what will measurement with what probability
(b) Find average value of energy.
(a) If energy is measured, the measurement is ℏω/2 and 3ℏω/2 with probability 1/2 and 1/2

|
37 videos|16 docs|19 tests
|
FAQs on One Dimensional System - Modern Physics
| 1. What is a free particle in one dimension? |  |
| 2. What is the step potential in quantum mechanics? |  |
| 3. What is a one-dimensional box in quantum mechanics? |  |
| 4. What is an infinite symmetric potential box? |  |
| 5. How is the graphical method used to analyze the square well finite potential box? |  |

|
Explore Courses for Physics exam
|

|








 which is eigen value associated with |ϕ1〉, |ϕ3〉, |ϕ5〉 respectively.
which is eigen value associated with |ϕ1〉, |ϕ3〉, |ϕ5〉 respectively.













































