Kinetic Theory of Gases | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Kinetic Theory |

|
| Gas Laws |

|
| Kinetic Energy of a Gas |

|
| Law of Equipartition of Energy and Mean Free Path |

|
| Degrees of Freedom |

|
| Specific Heat Capacity |

|
| Mean Free Path |

|
Introduction
- It says that the molecules of gas are in random motion and are continuously colliding with each other and with the walls of the container.
- All the collisions involved are elastic in nature due to which the total kinetic energy and the total momentum both are conserved.
- No energy is lost or gained from collisions.
Ideal Gas Equation

The ideal gas equation is as follows
PV = nRT
the ideal gas law relates the pressure, temperature, volume, and number of moles of ideal gas. Here R is a constant known as the universal gas constant.
Assumptions
- The gas consists of a large number of molecules, which are in random motion and obey Newton’s laws of motion.
- The volume of the molecules is negligibly small compared to the volume occupied by the gas.
- No forces act on the molecules except during elastic collisions of negligible duration.
- At the ordinary temperature and pressure, the molecular size is very very small as compared to the intermolecular distance.
- In case of gas, the molecules are very far from each other.
- So when the molecules are far apart and the size of the molecules is very small when compared to the distance between them.
- Therefore the interactions between the molecules are negligible.
- In case there is no interaction between the molecules, then there will be no force acting on the molecule.
- This is because it is not interacting with anything.
- Newton’s first law states that an object at rest will be at rest and an object will be in motion unless an external force acts upon it.
- So in this case, if the molecule is not interacting with any other molecule then there is nothing that can stop it.
- But sometimes when these molecules come close they experience an intermolecular force.
- So this basically something we call as a collision.
Solved Question
Q.1. The number of collisions of molecules of an ideal gas with the walls of the container is increasing per unit time. Which of the following quantities must also be increasing?
I. pressure
II. temperature
III. the number of moles of gas.
(a) I only
(b) I and II only
(c) II only
(d) II and III only
Ans: (a)
Solution: If there are more collisions between the molecules and the walls of the container, there must be more pressure against the wall. If there are more collisions than the molecules must have high average kinetic energy. Since kinetic energy is proportional to temperature, the temperature is also increasing.
Q.2. When the volume of a gas is decreased at constant temperature the pressure increases because of the molecules
(a) Strike unit area of the walls of the container more often
(b) Strike unit area of the walls of the container with higher speed
(c) Move with more kinetic energy
(d) Strike unit area of the walls of the container with less speed
Ans: (a)
Solution: The kinetic theory of the molecules depends on the temperature and since here the temperature remains constant, the pressure cannot increase due to the other options mentioned. So option A is correct as more pressure is generated here and hence pressure increases.
Kinetic Theory
Assumptions of Kinetic Theory of Gases:
- Every gas consists of extremely small particles known as molecules.
- The molecules of a given gas are all identical but are different from those of another gas.
- The molecules of a gas are identical, spherical, rigid, and perfectly elastic point masses.
- Their molecular size is negligible in comparison to intermolecular distance (10-9 m).
- The speed of gas molecules lies between zero and infinity (very high speed).

- The distance covered by the molecules between two successive collisions is known as free path and the mean of all free paths is known as mean free path.
- The number of collisions per unit volume in a gas remains constant.
- No attractive or repulsive force acts between gas molecules.
- Gravitational to extremely attraction among the molecules is ineffective due to small masses and very high speed of molecules.
Gas Laws
Assuming permanent gases to be ideal, through experiments, it was established that gases irrespective of their nature obey the following laws.
Boyle’s Law
At constant temperature the volume (V) of given mass of a gas is inversely proportional to its pressure (p), i.e.,
V ∝ 1/p ⇒ pV = constant
For a given gas, p1V1 = p2V2
 Fig: Boyle's law
Fig: Boyle's law
Charles’ Law
At constant pressure the volume (V) of a given mass of gas is directly proportional to its absolute temperature (T), i.e.,
V ∝ T ⇒ V / T = constant
For a given gas, V1/T1 = V2/T2
At constant pressure the volume (V) of a given mass of a gas increases or decreases by 1/273.15 of its volume at 0°C for each 1°C rise or fall in temperature.
 Fig: Charles' law
Fig: Charles' law
Volume of the gas at t°Celsius:
Vt = V0 (1 + t/273.15)
where V0 is the volume of gas at 0°C.
Gay Lussacs’ Law
At constant volume, the pressure p of a given mass of gas is directly proportional to its absolute temperature T, i.e. ,
p ∝ T ⇒ V/T = constant
For a given gas,
p1/T1 = p2/T2
At constant volume (V) the pressure p of a given mass of a gas increases or decreases by 1/273.15 of its pressure at 0°C for each l°C rise or fall in temperature.
 Fig: Gay Lussacs' law
Fig: Gay Lussacs' law
Volume of the gas at t°C, pt = p0 (1 + t/273.15)
where P0 is the pressure of gas at 0°C.
Avogadro’s Law
Avogadro stated that equal volume of all the gases under similar conditions of temperature and pressure contain equal number molecules. This statement is called Avogadro’s hypothesis. According to Avogadro’s law,
(i) Avogadro’s number: The number of molecules present in 1g mole of a gas is defined as Avogadro’s number.
NA = 6.023 X 1023 per gram mole
(ii) At STP or NTP (T = 273 K and p = 1 atm 22.4 L of each gas has 6.023 x 1023molecules.
(iii) One mole of any gas at STP occupies 22.4 L of volume.
Grahm's law of diffusion
When two gases at the same pressure and temperature are allowed to diffuse into each other, the rate of diffusion of each gas is inversely proportional to the square root of the density of the gas i.e.

Dalton's law of partial pressure
The total pressure exerted by a mixture of non-reacting gases occupying a vessel is equal to the sum of the individual pressures which each gas exerts if it alone occupied the same volume at a given temperature.
Standard or Perfect Gas Equation
Gases which obey all gas laws in all conditions of pressure and temperature are called perfect gases.
Equation of perfect gas pV=nRT
where p = pressure, V = volume, T = absolute temperature, R = universal gas constant and n = number of moles of a gas.
Universal gas constant R = 8.31 J mol-1K-1.
Real Gases
Real gases deviate slightly from ideal gas laws because:
- Real gas molecules attract one another.
- Real gas molecules occupy a finite volume.
Real or Van der Waal’s Gas Equation
(p + a/V2) (V – b) = RT
where a and b are called Van der Waal's constants.
Pressure due to an ideal gas is given by
p = (1/3).(mn/V). c2 = 1/3 ρ c2
For one mole of an ideal gas
P = (1/3).(M/V).c2
where, m = mass of one molecule, n = number of molecules, V = volume of gas, c = (c12+ c22 + … + cn2) / n all the root mean square (rms) velocity of the gas molecules and M = molecular weight of the gas. If p is the pressure of the gas and E is the kinetic energy per unit volume is E, then
p = (2/3).E
Kinetic Energy of a Gas
(i) Average kinetic energy of translation per molecule of a gas is given by:
E = (3/2) kt
where k = Boltzmann’s constant.
(ii) Average kinetic energy of translation per mole of a gas is given by:
E = (3/2) Rt
where R = universal gas constant.
(iii) For a given gas kinetic energy
E ∝ T ⇒ E1/E2 = T1/T2
(iv) Root mean square (rms) velocity of the gas molecules is given by:

(v) For a given gas c ∝ √T
(vi) For different gases c ∝1/√M
(vii) Boltzmann’s constant k = R/N
where R is ideal gas constant and N = Avogadro number.
Value of Boltzmann’s constant is 1.38 x 10-28 J/K.
(viii) The average speed of molecules of a gas is given by

(ix) The most probable speed of molecules of a gas is given by
⇒ 
Important Points:
(i) With rise in temperature rms speed of gas molecules increases as
(ii) With the increase in molecular weight rms speed of gas molecule decrease as(iii) Rms speed of gas molecules is of the order of knn/s, eg., at NTP for
hydrogen gas(iv) Rms speed of gas molecules does not depend on the pressure of gas !if temperature remains constant) because p ∝ p (Boyle s law). If pressure is increased n times, then density will also increase by n times but vrms remains constant.
Deviations from Ideal Behaviour
An ideal gas is one which obeys the gas laws of the gas equation PV = RT at all pressure and temperatures. However, no gas in nature is ideal. Almost all gases show significant deviations from the ideal behaviour. Thus the gases H2, N2 and CO2 which fail to obey the ideal-gas equation are termed as non-ideal or real gases.
Compressibility Factor : The extent to which a real gas departs from the ideal behaviour may be depicted in terms of a new function called the compressibility factor, denoted by Z. It is defined as

The deviations from ideality may be shown by a plot of the compressibility factor Z, against P.
For an ideal gas, Z = 1 and it is independent of temperature and pressure.
The deviations from ideal behaviour of a real gas will be determined by the value of Z being greater or less than 1.
The difference between unity and the value of the compressibility factor of a gas is a measure of the degree of non-ideality of the gas.
For a real gas, the deviations from ideal behaviour depends on :
(i) pressure
(ii) temperature.
This will be illustrated by examining the compressibility curves of some gases discussed below with the variation of pressure and temperature.
Effect of Pressure Variation on Deviations:

Effect of Temperature on Deviations:

From the above curves we can conclude that:
1. At low pressure and fairly high temperatures, real gases show nearly ideal behaviour and the ideal-gas equation is obeyed.
2. At low temperatures and sufficiently high pressures, a real gas deviates significantly from ideality and the ideal-gas equation is no longer valid.
3. The closer the gas is to the liquefaction point, the larger will be the deviation from the ideal behaviour.
Greater is the departure of Z from unity, more is the deviation from ideal behaviour.
(i) When Z < 1, this implies that gas is more compressible.
(ii) When Z > 1, this means that gas is less compressible.
(iii) When Z = 1, the gas is ideal.
Vander Waals Equation of State for a Real Gas: The equation of state generated by Vander Waals in 1873 reproduces the observed behaviour with moderate accuracy. For n moles of gas, the Vander Waals equation is
 (V - nb) = nRT
(V - nb) = nRT
where a and b are constants characteristic of a gas. This equation can be derived by considering a real gas and converting it to an ideal gas.
Volume Correction :
We know that for an ideal gas P x V = nRT. Now in a real gas the molecular volume cannot be ignored and therefore let us assume that b is the volume excluded (out of the volume of container) for the moving gas molecules per mole of a gas. Therefore due to n moles of a gas the volume excluded would be nb.
In a real gas in a container of volume V has only available volume of (V - nb) and this can be thought of, as an ideal gas in a container of volume (V - nb).
Pressure Correction:
- Let us assume the real gas exerts a pressure P. The molecules that exert the force on the container will get attracted by molecules of the immediate layer which are not assumed to be exerting pressure.
- It can be seen that the pressure the real gas exerts would be less than the pressure an ideal gas would have exerted. Therefore, if a real gas exerts a pressure P, then an ideal gas would exert a pressure equal to Pp (where p is the pressure lost by the gas molecules due to attractions). This small pressure p would be directly proportional to the extent of attraction between the molecules which are hitting the container wall and the molecules which are attracting these.
- Therefore:
- concentration of molecules which are hitting the container's wall
- concentration of molecules which are attracting these molecules
- where a is the constant of proportionality which depends on the nature of gas. Higher value of a reflects the increased attraction between gas molecules.
- The Vander Waals constantb (the excluded volume) is actually 4 times the volume of a single molecule. i.e. b = 4 NAV where NA is the Avogadro number.
- b = 4 x 6.023 x 1023, where r is the radius of a molecule.
The constant a and b: Vander Waals constant for attraction (A) and volume (B) are characteristic for a given gas. Some salient features of `a' and `b' are:
(i) For a given gas Vander Waal's constant of attraction `a' is always greater than Vander Waals constant of volume (B).
(ii) The gas having higher value of `a' can be liquified easily and therefore H2 and He are not liquified easily.
(iii) The units of a = litre2 atm mole-2 and that of b = litre mole-1
(iv) The numerical values of a and b are in the order of 10-1 to 10-2 to 10-4 respectively.
(v) Higher is the value of `a' for a given gas, easier is the liquefaction.
Explanation of deviation by Vander Waals equation
(i) At lower pressure : `V' is large and `b' is negligible in comparison with V.
Then Vander Waals equation reduces to :
 ⇒
⇒ 
 ⇒ z =
⇒ z =  = 1 -
= 1 - 
or PV < RT at low pressure (below Boyle temperature)
this accounts for the dip in PV vs P isotherm at low pressure.
(ii) At fairly high pressures : may be neglected in comparison with P.
may be neglected in comparison with P.
The Vander Waals equation becomes
P ( V-b) = RT ⇒ PV - Pb = RT
PV = RT Pb ⇒ z =  = 1
= 1 
or PV > RT at higher pressure (above Boyle temperature)
This accounts for the rising parts of the PV vs P isotherm at high pressures.
(iii) At very low pressure : V becomes so large that both b and become negligible and the Vander Waals equation reduces to PV = RT
 At extremely low pressure (at Boyle temperature)
At extremely low pressure (at Boyle temperature)
This shows why gases approach ideal behaviour at very low pressures.
(iv) Hydrogen and Helium : These are two lightest gases known. Their molecules have very small masses. The attractive forces between such molecules will be extensively small. So  is negligible even at ordinary temperatures. Thus PV > RT.
is negligible even at ordinary temperatures. Thus PV > RT.
Dieterici Equation :
P (V - nb) = n R T ea/VRT (for `n' mole of a gas)
Berthelot Equation :
 (V - nb) = n R T
(V - nb) = n R T
Virial Equation Of State For 1 Mole Of Gas :
z =  = 1 B
= 1 B  C
C  D
D  ..............
..............
B = second virial co-efficient , temperature dependent = b -
C = third virial co - efficient, temperature dependent = b2
Q.3. The compressibility factor for 1 mole of a van der Waals gas at 0xC and 100 atm pressure is found to be 0.5. Assuming that the volume of a gas molecule is negligible, calculate the van der Waals constant, a.
Ans: For 1 mole of the gas,
Z =  ⇒ 0.5 =
⇒ 0.5 =  ; V = 0.112 L
; V = 0.112 L
Neglecting b, van der Waals equation reduces to 
or pV +  = RT
= RT
or 100 x 0.112 +  = .0821 x 273
= .0821 x 273
a = 1.25 L2atm mol-2
Law of Equipartition of Energy and Mean Free Path
A single atom is free to move in space along the X, Y and Z axis. However, each of these movements requires energy. This is derived from the energy held by the atom. The Law of Equipartition of Energy defines the allocation of energy to each motion of the atom (translational, rotational and vibrational). Before we understand this law, let’s understand a concept called ‘Degrees of Freedom’.
Degrees of Freedom
- Imagine a single atom. In a three dimensional space, it can move freely along the X, Y and Z axis. Motion from one point to another is also known as translation. Hence, this movement along the three axes is called translational movement. If you have to specify the location of this atom, then you need three coordinates (x, y, and z).
We can also say that a single atom has 3 Degrees of Freedom. Most monoatomic molecules (i.e. molecules having a single atom like Argon) have 3 translational degrees of freedom, provided their movement is unrestricted.
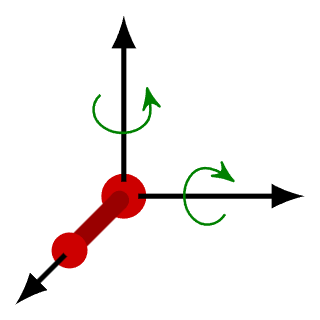
- Let’s now imagine a diatomic molecule (a molecule having two atoms like O2 or N2). Apart from the three translational degrees of freedom, these molecules can also rotate around the centre of mass. Two such rotations are possible along the axis normal to the axis that joins the two atoms.
- This adds two additional degrees of freedom (rotational) to the molecule. In simpler words, to specify the location of the molecule, you would need the X, Y and Z coordinates along with the rotational coordinates of the individual atoms.
It is important to note here that these diatomic molecules are not rigid rotators (where molecules do not vibrate) at all temperatures.
 Degree of freedom for different gases
Degree of freedom for different gases
- Along with the translational and rotational movements, diatomic molecules also oscillate along the interatomic axis like a single dimensional oscillator. This adds a vibrational degree of freedom to such molecules.
- Hence, to specify the location of a diatomic molecule, you would finally need the X, Y and Z coordinates along with the rotational and vibrational coordinates. So, in a nutshell, Degrees of Freedom is nothing but the number of ways in which a molecule can move. This forms the basis of the Law of Equipartition of Energy.
Law of Equipartition of Energy
- The law states that: “In thermal equilibrium, the total energy of the molecule is divided equally among all Degrees of Freedom of motion”. Before delving into the calculations, let’s understand the law better. If a molecule has 1000 units of energy and 5 degrees of freedom (which includes translational, rotational and vibrational movements), then the molecule allocates 200 units of energy to each motion.
 Law of Equipartition of EnergyNow, let us look at some equations!
Law of Equipartition of EnergyNow, let us look at some equations!
- Kinetic Energy of a single molecule: KE = 1/2 mv2. A gas in thermal equilibrium at temperature T, the average Energy is:
Eavg = 1/2 mvx2 + 1/2 mvy2 + 1/2 mvz2 = 1/2KT + 1/2 KT + 1/2 KT = 3/2 KT
where K = Boltzmann’s constant. In case of a monoatomic molecule, since there is only translational motion, the energy allotted to each motion is 1/2KT. This is calculated by dividing total energy by the degrees of freedom:
3/2 KT ÷ 3 = 1/2 KT - In case of a diatomic molecule, translational, rotational and vibrational movements are involved. Hence the Energy component of translational motion= 1/2 mvx2 + 1/2 mvy2 + 1/2 mvz2. Energy component of rotational motion= 1/2 I1w12 + 1/2 I2w22 {I1 & I2 moments of inertia. w1 & w2 are angular speeds}
- And, the energy component of vibrational motion= 1/2 m (dy/dt)2+ 1/2 ky2. Where k is the force constant of the oscillator and y is the vibrational coordinate. It is important to note here that this has both kinetic and potential modes.
- According to the Law of Equipartition of Energy, in thermal equilibrium, the total energy is distributed equally among all energy modes. While the translational and rotational motion contributes ½ KT to the total energy, vibrational motion contributes 2 x 1/2KT = KT since it has both kinetic and potential energy modes.
Solved Question
Q.4. ‘N′ moles of a diatomic gas in a cylinder are at a temperature ′T′. Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monatomic gas. What is the change in the total kinetic energy of the gas?
(a) 5/2 nRT
(b) 1/2 nRT
(c) 0
(d) 3/2 nRT
Ans: (d)
Solution: Initial K.E. = (3/2) nRT . Number of moles in the final sample = 2n
Since the gas is changed to monoatomic gas, we have: K.E. of the final sample = (3/2) × 2nRT
Hence, the change in the K.E. = 3nRT – (3/2) nRT = 3/2 nRT.
Specific Heat Capacity
- Specific Heat Capacity is the amount of energy required by a single unit of a substance to change its temperature by one unit.
- When you supply energy to a solid, liquid or gas, its temperature changes.
- This change of temperature will be different for different substances like water, iron, oxygen gas, etc.
- This energy is known as the Specific Heat Capacity of the substance and is denoted by ‘C’.
- Molar Specific Heat Capacity of a substance is C and is calculated for one mole of the substance.
- Mathematically we can write: C = ΔQ/m
- Further, when you supply energy to a substance, it may undergo a change in volume and/or pressure, especially in gaseous substances.
- Hence, to determine the Specific Heat Capacity of gases, it is important to pre-determine the pressure and volume under which you want to calculate C since it can have infinite values (depending on the values of pressure and volume).
- The Molar Specific Heat Capacity at constant volume is denoted by Cv and that at constant pressure is denoted by Cp.
Specific Heat Capacity of Gases
According to the first law of thermodynamics ΔQ = ΔU + ΔW {change in heat of a system = change in internal energy + amount of work done}. Change in heat of a system (ΔQ) can also be calculated by multiplying Mass (m), Specific Heat Capacity (C) and change in Temperature (ΔT):
ΔQ = mCΔT Or,
mCΔT = ΔU + ΔW ————(1)
Monatomic Gases
- In monatomic gas, molecules have three translational degrees of freedom. At temperature T, the average energy of a monatomic molecule is (3/2)KBT.
- Now, let’s look at one mole of such a gas at constant volume and calculate the internal energy (U):
- U = (3/2) KBT x NA {where NA is Avogadro constant}
- The total internal energy will be the internal energy of a single molecule multiplied by the number of molecules in one mole of the gas; which is Avogadro constant NA.
- Now, Boltzmann’s constant (KB) is the Gas constant (R) divided by NA. Hence:
- U = (3/2)(R/NA)T × NA
- U = (3/2)RT ——————(2)
- In equation (1), since the energy is supplied at constant volume: mCvΔT = ΔU + ΔW.
- For one mole of a gas, m = 1. Also, for calculating Cv, ΔT = 1.
- Since the volume is constant, ΔW = 0. Therefore, 1×Cv×1 = ΔU + 0
- Cv = ΔU = (3/2)RT ——————[refer (2)]
- So, the molar specific heat capacity to change the temperature by 1 unit would be Cv = (3/2)R.
- For an ideal gas, Cp – Cv = R (Gas Constant).
- Therefore: Cp = R + Cv = R + (3/2)R = (5/2)R.
- The ratio of Cp:Cv (γ) is hence 5:3.
Diatomic Gases
In case of diatomic gases, there are two possibilities:
- Molecule is a Rigid Rotator: In this scenario, the molecule will have five degrees of freedom (3 translational and two rotational). As defined by the Law of Equipartition of Energy, the internal energy (U) can be calculated as:
U = (5/2)KBT * NA = (5/2)RT. Following the calculation used for monatomic gases:
Cv = (5/2)R
Cp = (7/2)R
γ = 7:5
- Molecule is NOT a Rigid Rotator: In this scenario, the molecule will have an additional vibrational degree of freedom. The internal energy can thus be calculated as:
U = [(5/2)KBT + KBT] * NA = [(5/2)(R/NA)T + (R/NA)T] * NA = (7/2)RT
Following the calculation used for monatomic gases: Cv = (7/2)R
Cp = (9/2)R and hence γ = 9:7
Polyatomic Gases
The degrees of freedom of polyatomic gases are:
- 3 translational
- 3 rotational
- f vibrational
Deploying the Law of Equipartition of Energy for calculation of internal energy, we get:
U = [(3/2)KBT + (3/2)KBT + fKBT] * NA = [(3/2)(R/NA)T + (3/2)(R/NA)T + f(R/NA)T] * NA
U = (3 + f)RT
The molar specific heat capacities:
Cv = (3+f)R
Cp = (5+f)R
Specific Heat Capacity of Solids
Using the Law of Equipartition of energy, the specific heat capacity of solids can be determined. Let us consider a mole of solid having NA atoms. Each atom is oscillating along its mean position. Hence, the average energy in three dimensions of the atom would be:
3 * 2 * (1/2)KBT = 3KBT
For one mole of solid, the energy would be:
U = 3KBT * NA = 3(R/NA)T * NA = 3RT —————–(3)
If the pressure is kept constant, then according to the laws of thermodynamics
ΔQ = ΔU + PΔV
In case of solids, the change in volume is ~0 if the energy supplied is not extremely high. Hence,
ΔQ = ΔU + P * 0 = ΔU
So, the molar specific heat capacity to change the temperature by 1 unit would be:
C = 3R ——————-[refer (3)]
Specific Heat Capacity of Water
For the purpose of calculation of specific heat capacity, water is treated as a solid. A water molecule has three atoms (2 hydrogens and one oxygen). Hence, its internal energy would be:
U = (3 * 3KBT)*NA = 9KBT*NA = 9(R/NA)T * NA = 9RT
And, following a similar calculation like solids: C = 9R
Mean Free Path
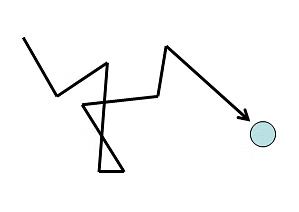
- The Kinetic theory of gases assumes that molecules are continuously colliding with each other and they move with constant speeds and in straight lines between two collisions. Hence, a molecule follows a chain of zigzag paths. Each of these paths is known as a free path (since it lies between two collisions).
- The average distance travelled by the molecule between two collisions is known as the Mean Free Path. The number of collisions increases if the gas is denser or the molecules are large in size.
 Mean Free Path
Mean Free Path - If the molecules of a gas are spheres having a diameter – ‘d’; one molecule is moving with an average speed – ‘v’ and the number of molecules per unit volume is “n”, then the mean free path (l) can be calculated by using the formula: l = 1/πnd2
- The equation is arrived at under the assumption that all other molecules are at rest, which is not actually the case. If we consider all molecules to be moving in all directions with different speeds, then the mean free path formula would be: l = 1/√2 πnd2
Q.5. One mole of an ideal monoatomic gas is mixed with 1 mole of an ideal diatomic gas. The molar specific heat of the mixture at constant volume is (in cal):
(a) 22 cal
(b) 4 cal
(c) 8 cal
(d) 12 cal
Ans: (b)
Solution: As we know Cv = (3/2) R for a monoatomic gas and Cv = (5/2) R for a diatomic case.
Thus for the mixture, average of both is = [(3/2) R + (5/2) R] /2 = 2R = 4 cal.
|
97 videos|378 docs|103 tests
|
FAQs on Kinetic Theory of Gases - Physics Class 11 - NEET
| 1. What is the Kinetic Theory of Gases and how does it explain the behavior of gas particles? |  |
| 2. What are the main gas laws derived from the Kinetic Theory? |  |
| 3. How is the kinetic energy of gas particles calculated and what does it represent? |  |
| 4. What is the Law of Equipartition of Energy and how does it apply to gases? |  |
| 5. What is the mean free path in the context of the Kinetic Theory of Gases? |  |

|
Explore Courses for NEET exam
|

|