Law of Equipartition of Energy & Mean Free Path | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Degrees of Freedom |

|
| Law of Equipartition of Energy |

|
| Specific Heat Capacity |

|
| Specific Heat Capacity of Solids |

|
| Specific Heat Capacity of Water |

|
| Mean Free Path |

|
| Solved Question |

|
A single atom is free to move in space along the X, Y and Z axis. However, each of these movements requires energy. This is derived from the energy held by the atom. The Law of Equipartition of Energy defines the allocation of energy to each motion of the atom (translational, rotational and vibrational). Before we understand this law, let’s understand a concept called ‘Degrees of Freedom’.
Degrees of Freedom
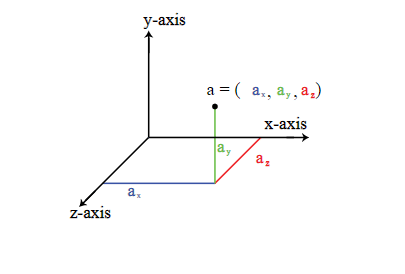
- Imagine a single atom. In a three dimensional space, it can move freely along the X, Y and Z axis. Motion from one point to another is also known as translation. Hence, this movement along the three axes is called translational movement. If you have to specify the location of this atom, then you need three coordinates (x, y, and z).
We can also say that a single atom has 3 Degrees of Freedom. Most monoatomic molecules (i.e. molecules having a single atom like Argon) have 3 translational degrees of freedom, provided their movement is unrestricted.
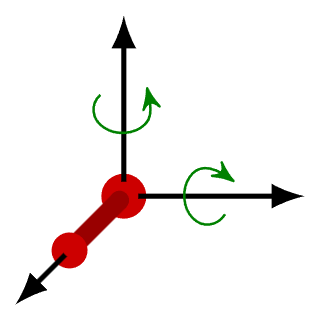
- Let’s now imagine a diatomic molecule (a molecule having two atoms like O2 or N2). Apart from the three translational degrees of freedom, these molecules can also rotate around the centre of mass. Two such rotations are possible along the axis normal to the axis that joins the two atoms.
- This adds two additional degrees of freedom (rotational) to the molecule. In simpler words, to specify the location of the molecule, you would need the X, Y and Z coordinates along with the rotational coordinates of the individual atoms.
It is important to note here that these diatomic molecules are not rigid rotators (where molecules do not vibrate) at all temperatures. - Along with the translational and rotational movements, diatomic molecules also oscillate along the interatomic axis like a single dimensional oscillator. This adds a vibrational degree of freedom to such molecules.
- Hence, to specify the location of a diatomic molecule, you would finally need the X, Y and Z coordinates along with the rotational and vibrational coordinates. So, in a nutshell, Degrees of Freedom is nothing but the number of ways in which a molecule can move. This forms the basis of the Law of Equipartition of Energy.
Law of Equipartition of Energy
- The law states that: “In thermal equilibrium, the total energy of the molecule is divided equally among all Degrees of Freedom of motion”. Before delving into the calculations, let’s understand the law better. If a molecule has 1000 units of energy and 5 degrees of freedom (which includes translational, rotational and vibrational movements), then the molecule allocates 200 units of energy to each motion.
 Law of Equipartition of EnergyNow, let us look at some equations!
Law of Equipartition of EnergyNow, let us look at some equations!
- Kinetic Energy of a single molecule: KE = 1/2 mv2. A gas in thermal equilibrium at temperature T, the average Energy is:
Eavg = 1/2 mvx2 + 1/2 mvy2 + 1/2 mvz2 = 1/2KT + 1/2 KT + 1/2 KT = 3/2 KT
where K = Boltzmann’s constant. In case of a monoatomic molecule, since there is only translational motion, the energy allotted to each motion is 1/2KT. This is calculated by dividing total energy by the degrees of freedom:
3/2 KT ÷ 3 = 1/2 KT - In case of a diatomic molecule, translational, rotational and vibrational movements are involved. Hence the Energy component of translational motion= 1/2 mvx2 + 1/2 mvy2 + 1/2 mvz2. Energy component of rotational motion= 1/2 I1w12 + 1/2 I2w22 {I1 & I2 moments of inertia. w1 & w2 are angular speeds}
- And, the energy component of vibrational motion= 1/2 m (dy/dt)2+ 1/2 ky2. Where k is the force constant of the oscillator and y is the vibrational coordinate. It is important to note here that this has both kinetic and potential modes.
- According to the Law of Equipartition of Energy, in thermal equilibrium, the total energy is distributed equally among all energy modes. While the translational and rotational motion contributes ½ KT to the total energy, vibrational motion contributes 2 x 1/2KT = KT since it has both kinetic and potential energy modes.
Solved Question
Q. ‘N′ moles of a diatomic gas in a cylinder are at a temperature ′T′. Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas get converted into monatomic gas. What is the change in the total kinetic energy of the gas?
(a) 5/2 nRT
(b) 1/2 nRT
(c) 0
(d) 3/2 nRT
Ans: (d)
Solution: Initial K.E. = (3/2) nRT . Number of moles in the final sample = 2n
Since the gas is changed to monoatomic gas, we have: K.E. of the final sample = (3/2) × 2nRT
Hence, the change in the K.E. = 3nRT – (3/2) nRT = 3/2 nRT.
Specific Heat Capacity
Specific Heat Capacity is the amount of energy required by a single unit of a substance to change its temperature by one unit. When you supply energy to a solid, liquid or gas, its temperature changes. This change of temperature will be different for different substances like water, iron, oxygen gas, etc.
This energy is known as the Specific Heat Capacity of the substance and is denoted by ‘C’. Molar Specific Heat Capacity of a substance is C and is calculated for one mole of the substance. Mathematically we can write:
C = ΔQ/m
Further, when you supply energy to a substance, it may undergo a change in volume and/ or pressure, especially in gaseous substances. Hence, to determine the Specific Heat Capacity of gases, it is important to pre-determine the pressure and volume under which you want to calculate C since it can have infinite values (depending on the values of pressure and volume). The Molar Specific Heat Capacity at constant volume is denoted by Cv and that at constant pressure is denoted by Cp.
Specific Heat Capacity of Gases
According to the first law of thermodynamics ΔQ = ΔU + ΔW {change in heat of a system = change in internal energy + amount of work done}. Change in heat of a system (ΔQ) can also be calculated by multiplying Mass (m), Specific Heat Capacity (C) and change in Temperature (ΔT):
ΔQ = mCΔT Or,
mCΔT = ΔU + ΔW ————(1)
Monatomic Gases (Monoatomic gases)
In monatomic gas, molecules have three translational degrees of freedom. At temperature ‘T’ the average energy of a monatomic molecule is (3/2)KBT. Now, let’s look at one mole of such a gas at constant volume and calculate the internal energy (U):
U = (3/2) KBT x NA {where NA is Avogadro constant}
The total internal energy will by the internal energy of a single molecule multiplied by the number of molecules in one mole of the gas; which is Avogadro constant NA. Now, Boltzmann’s constant (KB) is the Gas constant (R) divided by NA. Hence: U = (3/2)(R/NA)T × NA
U = (3/2)RT ———————(2)
In equation (1), since the energy is supplied at constant volume: mCvΔT = ΔU + ΔW. For one mole of a gas, m = 1. Also, for calculating Cv, ΔT = 1. Since the volume is constant, ΔW = 0. Therefore, 1×Cv×1 = ΔU + 0
Cv = ΔU = (3/2)RT —————-[refer (2)]
So, the molar specific heat capacity to change the temperature by 1 unit would be Cv = (3/2)R. For an ideal gas, Cp – Cv = R (Gas Constant). Therefore: Cp = R + Cv = R + (3/2)R = (5/2)R. The ratio of Cp:Cv (γ) is hence 5:3.
Diatomic Gases
In case of diatomic gases, there are two possibilities:
- Molecule is a Rigid Rotator: In this scenario, the molecule will have five degrees of freedom (3 translational and two rotational). As defined by the Law of Equipartition of Energy, the internal energy (U) can be calculated as:
U = (5/2)KBT * NA = (5/2)RT. Following the calculation used for monatomic gases:
Cv = (5/2)R
Cp = (7/2)R
γ = 7:5
- Molecule is NOT a Rigid Rotator: In this scenario, the molecule will have an additional vibrational degree of freedom. The internal energy can thus be calculated as:
U = [(5/2)KBT + KBT] * NA = [(5/2)(R/NA)T + (R/NA)T] * NA = (7/2)RT
Following the calculation used for monatomic gases: Cv = (7/2)R
Cp = (9/2)R and hence γ = 9:7
Polyatomic Gases
The degrees of freedom of polyatomic gases are:
- 3 translational
- 3 rotational
- f vibrational
Deploying the Law of Equipartition of Energy for calculation of internal energy, we get:
U = [(3/2)KBT + (3/2)KBT + fKBT] * NA = [(3/2)(R/NA)T + (3/2)(R/NA)T + f(R/NA)T] * NA
U = (3 + f)RT
The molar specific heat capacities:
Cv = (3+f)R
Cp = (5+f)R
Specific Heat Capacity of Solids
Using the Law of Equipartition of energy, the specific heat capacity of solids can be determined. Let us consider a mole of solid having NA atoms. Each atom is oscillating along its mean position. Hence, the average energy in three dimensions of the atom would be:
3 * 2 * (1/2)KBT = 3KBT
For one mole of solid, the energy would be:
U = 3KBT * NA = 3(R/NA)T * NA = 3RT —————–(3)
If the pressure is kept constant, then according to the laws of thermodynamics
ΔQ = ΔU + PΔV
In case of solids, the change in volume is ~0 if the energy supplied is not extremely high. Hence,
ΔQ = ΔU + P * 0 = ΔU
So, the molar specific heat capacity to change the temperature by 1 unit would be:
C = 3R ——————-[refer (3)]
Specific Heat Capacity of Water
For the purpose of calculation of specific heat capacity, water is treated as a solid. A water molecule has three atoms (2 hydrogens and one oxygen). Hence, its internal energy would be:
U = (3 * 3KBT)*NA = 9KBT*NA = 9(R/NA)T * NA = 9RT
And, following a similar calculation like solids: C = 9R
Mean Free Path
- The Kinetic theory of gases assumes that molecules are continuously colliding with each other and they move with constant speeds and in straight lines between two collisions. Hence, a molecule follows a chain of zigzag paths. Each of these paths is known as a free path (since it lies between two collisions).
- The average distance travelled by the molecule between two collisions is known as the Mean Free Path. The number of collisions increases if the gas is denser or the molecules are large in size.
 Mean Free Path
Mean Free Path - If the molecules of a gas are spheres having a diameter – ‘d’; one molecule is moving with an average speed – ‘v’ and the number of molecules per unit volume is “n”, then the mean free path (l) can be calculated by using the formula: l = 1/πnd2
- The equation is arrived at under the assumption that all other molecules are at rest, which is not actually the case. If we consider all molecules to be moving in all directions with different speeds, then the mean free path formula would be: l = 1/√2 πnd2
Solved Question
Q. One mole of an ideal monoatomic gas is mixed with 1 mole of an ideal diatomic gas. The molar specific heat of the mixture at constant volume is (in cal):
(a) 22 cal
(b) 4 cal
(c) 8 cal
(d) 12 cal
Ans: (b)
Solution: As we know Cv = (3/2) R for a monoatomic gas and Cv = (5/2) R for a diatomic case.
Thus for the mixture, average of both is = [(3/2) R + (5/2) R] /2 = 2R = 4 cal.
|
97 videos|378 docs|103 tests
|
FAQs on Law of Equipartition of Energy & Mean Free Path - Physics Class 11 - NEET
| 1. What is the Law of Equipartition of Energy? |  |
| 2. How does the Law of Equipartition of Energy relate to the concept of degrees of freedom? |  |
| 3. What are examples of degrees of freedom in a molecule? |  |
| 4. How does the Law of Equipartition of Energy apply to gases? |  |
| 5. What are the implications of the Law of Equipartition of Energy in understanding the behavior of matter? |  |

|
Explore Courses for NEET exam
|

|