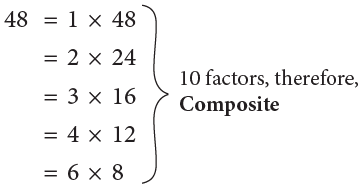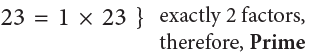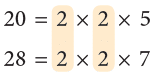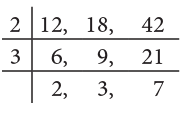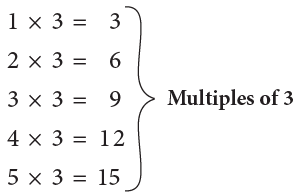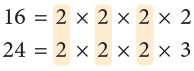Factors and Multiples Class 5 Notes Maths
Introduction
- Did you know that numbers follow patterns? Factors and multiples help us find these patterns!
- Factors show us how numbers can break apart, and multiples show us how they grow.
 Knowing these patterns makes math easier and fun! So, lets crack the code.
Knowing these patterns makes math easier and fun! So, lets crack the code.
Factor
- A factor is a number that divides another number exactly, without leaving any remainder.
- In simple words, if you multiply two numbers to get a product, then both of those numbers are called factors of the product.
- For example,
Factors of 10: 1, 2, 5, and 10.
This is because
10÷1=10,
and
Example : List all the factors of the following numbers.
(a) 16
(b) 17
(a) 16 = 1 × 16
= 2 × 8
= 4 × 4
∴ The factors of 16 are 1, 2, 4, 8 and 16.
(b) 17 = 1 × 17
∴ The factors of 17 are 1 and 17.
From the above example it is clear that,
- Every number has at least two factors—1 and the number itself.
- All the factors of a number are either less than or equal to the number.
Prime Number & Composite Number
Following are the definitions of prime and composite numbers
1. Prime Number
- A prime number is any natural number which has exactly two factors—1 and the number itself.
- For example,
13 = 1 × 13.
There are no other factors of 13, so 13 is a prime number
2. Composite Number
- Every natural number except 1 that has more than two different factors is called a composite number.
- For example,
- Check whether 4 is prime or composite number?
4 is a Composite Number because
Factors of 4 are 1, 2, 4
It can be divided by 1, 2, and 4.
EduRev Tip:
- The number 1 is neither prime nor composite.
- It is not a prime because it does not have exactly two factors
- It is not composite because it does not have more than two factors.
Sieve of Eratosthenes
A Greek mathematician, Eratosthenes, devised a method to find out prime numbers between 1 and 100. The steps used in this method are as follows:
The steps used in this method are as follows:
Step 1: Write all the numbers from 1 to 100 in a table as shown.
Step 2: Cross out 1 as it is not a prime number.
Step 3: Circle 2 and cross out multiples of 2.
Step 4: Circle 3 and cross out multiples of 3.
Step 5: Circle 5 and cross out multiples of 5.
Step 6: Circle 7 and cross out multiples of 7.
The circled numbers are all the prime numbers between 1 and 100.
EduRev Tips:
This method is called ‘The Sieve of Eratosthenes’ because factors are used to sift out certain numbers which are multiples just as a sieve sifts out chaff from wheat.
Example : Tell whether each of the numbers 48 and 23 is composite or prime.
Sol: 48 is a composite number whereas 23 is a prime number because of the following reason
Twin Primes & Co- Primes
The concept of twin primes and co- primes is mentioned below1. Twin Prime
- Twin Primes are the prime numbers that differ by 2.
- For example, 3 and 5, 5 and 7, 11 and 13, etc. are twin primes.
2. Co- Prime
- Two natural numbers are said to be co-primes, If they have only '1' as a common factor.
- For example, 2 and 3, 5 and 7, 3 and 4, 4 and 9, etc. are co-primes.
Prime Factorization
- Prime Factorization is the process of breaking down a composite number into its prime factors.
- An expression written as a product of its prime factors is called the prime factorization of that number.
- For Example, Prime factorization of 20 = 5 x 2 x 2
- There are basically two methods by which we can find prime factorization of any number
1. Factor Tree Method
2. Continuous Division Method
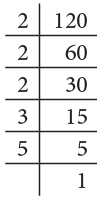
Example: Find the prime factorization of 120 (by factor tree method and division method)
Sol: We will first solve by factor tree method and then by division method
Method 1: Factor Tree
Step 1: Write the number to be factorized at the top.
Step 2: Choose any pair of factors as branches. If either of these factors is composite, factorize again.
Step 3: Choose a pair of factors of each composite number and continue the branches for prime factor(s).
Step 4: Keep factorizing till you have a row of prime factors.Conventionally, the prime factors are written in increasing order.
∴ The prime factorization of 120 = 2 × 2 × 2 × 3 × 5.
Method 2: Continuous Division
Step 1: Start dividing by the smallest prime factor until you cannot divide any more.
Step 2: Continue dividing by the next higher prime factor.
Step 3: Repeat the process till you get 1.∴ The prime factorization of 120 is 2 × 2 × 2 × 3 × 5.
Highest Common Factor (HCF)
- HCF stands for Highest Common Factor.
- It is the largest number that can divide two or more numbers exactly without leaving any remainder.
- For example, 4 × 2 = 8 and 4 × 5 = 20. So, 4 is a common factor of 8 and 20.
You can find the HCF of two or more numbers by different methods, as follows:
Method 1: By Listing Factors
Example : Find the HCF of 12 and 40.
Step 1: List all the factors of each number.
Factors of 12:,
, 3,
, 6 and 12
Factors of 40:5, 8, 10, 20 and 40.
Step 2: Identify common factors.
The common factors are 1, 2 and 4.
Step 3: Identify largest number in the list of common factors.
Out of these common factors, 4 is the largest.
∴ HCF of 12 and 40 is 4.
Method 2: By Prime Factorization
Example : Find the HCF of 20 and 28.
Step 1: List all the factors of each number by either method.
Step 2: Identify the common factors.
Step 3: HCF is the product of common prime factors.
∴ HCF of 20 and 28 = 2 × 2 = 4.
EduRev Tip:
You can get the prime factorization by making factor trees or by continuous division.
However, continuous division is the preferred method.
Method 3: By Division Method
Example: Find the HCF of 12, 18 and 42.
Step 1: Divide the numbers by common factors only.
Step 2: Stop dividing when there are no more common factors except 1.
Step 3: Find the product of common factors. 2, 3 and 7 do not have any common factor except 1, so stop division.
∴ HCF of 12, 18 and 42 = 2 × 3 = 6.
HCF of Large Numbers
It is easier to find the HCF of large numbers by division method.
Example 1 : Find the HCF of 217 and 686.
Step 1: Divide the greater number by the smaller number.
Step 2: Make the remainder the new divisor and the original divisor, the new dividend. Repeat the process until you get 0 as the remainder.
Step 3: The last divisor is the required HCF.
Here, the last divisor is 7.
So, the HCF of 217 and 686 is 7.
In case of three numbers, first find the HCF of any two numbers.
Then, take the last divisor of the two numbers and the remaining number and find their HCF.
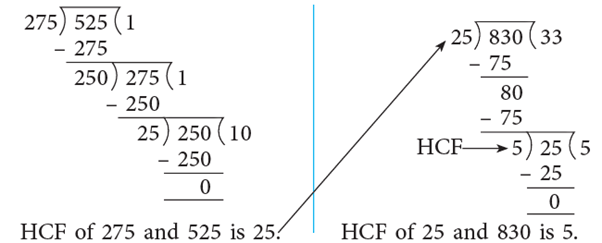
Example 2: Find the HCF of 275, 525 and 830.
First, we take 275 and 525. Now, find the HCF of 25 and 830.
∴ The HCF of 275, 525 and 830 is 5.
Multiple
- A multiple of a whole number is the product of the number and any counting number.
- We can state some multiples of 2 and 11 as:

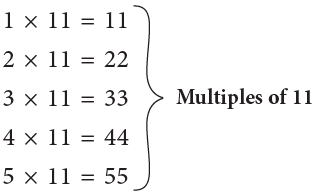
From the above discussion, we can observe these properties of multiples:
Did You Know
- Every number is a multiple of 1.
- The smallest multiple of any number (other than zero) is the number itself.
- Every multiple of a number is greater than or equal to that number.
- The number of multiples of a given number is infinite.
Example : Find the first five multiples of 3.
∴ The first five multiples of 3 are 3, 6, 9, 12 and 15.
Least Common Multiple (LCM)
- If a number is a multiple of two or more numbers, it is called a common multiple of the numbers.
- For example, 2 × 9 = 18.
∴ 18 is a common multiple of 2 and 9.
The smallest number (other than zero) that is a multiple of two or more counting numbers is the least common multiple (LCM) of the numbers. It is the least number which is divisible by all the given numbers.
You can find the LCM of two or more numbers by different methods, as follows:
Method 1: By Listing the Multiples
Example : Find the LCM of 3, 6 and 12.
Step 1: List some multiples of each number.
The multiples of 3 are 3, 6, 9,, 15, 18, 21,
27, 30, 33,
39, ...
The multiples of 6 are 6,, 18,
30,
42, 48, ...
The multiples of 12 are,
48, ...
Step 2: Identify common multiples.
Some common multiples of 3, 6 and 12 are 12, 24, 36, ...
Step 3: Pick up the least common multiple from the list of common multiples.
Out of these common multiples, 12 is the least.
∴ The least common multiple (LCM) of 3, 6 and 12 is 12.
Method 2: By Prime Factorisation
Example : Find the LCM of 16 and 24.
Step 1: Find the prime factorisation of each number.
Step 2: Identify the common factors.
Step 3: Multiply the common factors and the extra factors to get the LCM.
∴ LCM of 16 and 24 is 48.
Method 3: By Division Method
Example : Find the LCM of 20, 28 and 40.
Step 1: Divide the numbers by a prime factor common to at least 2 of the given numbers. Bring down the number as such, if it is not completely divisible by the prime factor.
Step 2: Stop dividing when there is no further common factor except 1.
Step 3: Find the product of the numbers in the left column and the last remainders.
∴ LCM of 20, 28 and 40 = 2 × 2 × 2 × 5 × 7 = 280.
Divisibility Rules
- If a number is a divisor of a second number, then the number is divisible by the first.
For example, since 3 is a divisor of 6, so 6 is divisible by 3. - If a number is not prime, then it would be divisible by a number smaller than itself. We can find out by actual division whether a number is divisible by another number or not.
- For example, if we divide 392 by 7, we find that the remainder is 0, so 392 is divisible by 7. In some cases, the process can be shortened by applying certain tests on the digits of the number.
 Below, we give some such tests:
Below, we give some such tests:
- Divisibility by 2
A number is divisible by 2 if its units digit is divisible by 2.
So, a number is divisible by 2 if its units digit is 0, 2, 4, 6 or 8. A number ending in 1, 3, 5, 7 or 9 is not divisible by 2.
For example, the numbers 120, 3172, 234, 81396, 105098 are all divisible by 2 while numbers like 13, 287, 335, 7091, 28469 are not divisible by 2. - Divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example, the number 384 is divisible by 3 and the sum of its digits (3 + 8 + 4) is 15, which is divisible by 3.
Similarly, the number 217095 is also divisible by 3 as the sum of its digits (2 + 1 + 7 + 0 + 9 + 5) is 24, which is divisible by 3.
The number 839 is not divisible by 3 as the sum of its digits (8 + 3 + 9) is 20, which is not divisible by 3. - Divisibility by 5
A number is divisible by 5 if its units digit is 0 or 5.
For example, the numbers like 205, 3075, 2370, 15000 are all divisible by 5. Numbers like 27, 3189, 200053 are not divisible by 5 as they do not end in 0 or 5. - Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
For example, the number 7326 is divisible by 9, because 7 + 3 + 2 + 6 = 18 and 18 is divisible by 9. The number 27041 is not divisible by 9, because the sum of its digits 2 + 7 + 0 + 4 + 1 = 14, which is not divisible by 9. - Divisibility by 10
A number is divisible by 10 if its units digit is 0.
For example, the numbers 100, 8390, 9500, 5401,000 are all divisible by 10. Numbers like 209, 703001, 28597, 4385 are not divisible by 10 as their units digit is not 0. - Divisibility by 11
A number is divisible by 11 if the difference of the sum of its digits in odd places and the sum of its digits in even places (starting from the units place) is either 0 or divisible by 11.
Study the following table.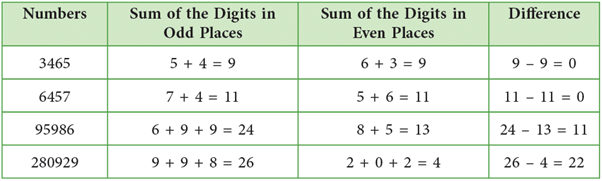
So, the numbers 3465, 6457, 95986 and 280929 are all divisible by 11.
Below, we give rules to test the divisibility of a number by composite numbers like 4, 6, 8, 12 and 25:
- Divisibility by 4
A number is divisible by 4 if the number formed by its digits in tens and units places is divisible by 4.
For example, in the number 80372, the number 72 formed by the tens and the units digit 2 is divisible by 4. As you can check this number is divisible by 4. - Divisibility by 6
A number is divisible by 6 if it is divisible by both 2 and 3, i.e., it should be an even number and the sum of its digits should be divisible by 3.
For example, the number 68370 is divisible by 6. It is an even number and also sum of its digits (6 + 8 + 3 + 7 + 0) is 24, which is divisible by 3. - Divisibility by 8
A number is divisible by 8 if the number formed by the digits at the hundreds, tens and units place is divisible by 8.
Consider the number 207608.
The number formed by the digits at the hundreds, tens and units place, i.e., 608 is divisible by 8.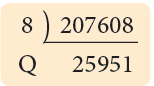
∴ This number is divisible by 8.
Since 705 is not divisible by 8, so the number 8705 is not divisible by 8.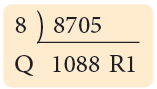
- Divisibility by 25
A number is divisible by 25 if the number formed by the digits at the tens and units places is divisible by 25.
For example, in the numbers 8750, 23275, 8926825, we observe that 50, 75 and 25, i.e., the numbers formed by the digits at the tens and units places, are divisible by 25. So, all these numbers are divisible by 25.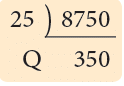
From the above rules, we observe that:
A number is divisible by another number if it is divisible by its co-prime factors.
Thus, number divisible by 2 and 5 will also be divisible by 10.
Example 13: Check the divisibility of 19440 by 18.
The co-prime factors of 18 are 2 and 9.
Therefore, to check the divisibility of 19440 by 18, we check whether the given number is divisible by 2 and 9 both.
19440: It is an even number and so is divisible by 2.
Sum of the digits = 1 + 9 + 4 + 4 + 0
= 18, which is divisible by 9, so
19440 is also divisible by 9.
Thus, 19440 is divisible by 2 × 9, i.e., 18.
|
95 videos|462 docs|47 tests
|
FAQs on Factors and Multiples Class 5 Notes Maths
| 1. What are prime numbers and composite numbers? |  |
| 2. What are twin primes and co-primes? |  |
| 3. How do you perform prime factorization? |  |
| 4. What is the highest common factor (HCF) and how do you find it? |  |
| 5. How do you calculate the least common multiple (LCM) of two numbers? |  |