Phase Transition & Low Temperature Physics | Kinetic Theory & Thermodynamics PDF Download
| Table of contents |

|
| Third Law of Thermodynamics & Attainable of Low Temperature |

|
| Production of Low Temperature by the Joule – Kelvin Expansion |

|
| Phase Transition |

|
| Second Order Phase Transition |

|
Third Law of Thermodynamics & Attainable of Low Temperature
The third law of thermodynamics is some time stated as follows:
It is impossible for any process no matter how idealized the process is to reduce the entropy of a system to its zero point value in a finite number of operations.
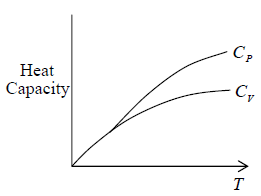
Properties of material at low temperature
At T → 0
CP = CV = 0
At T → 0
S→0
At T → 0
Thermal expansion coefficient α = 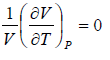
Production of Low Temperature by the Joule – Kelvin Expansion
The Joule – Kelvin Expansion is essentially a continuous steady state flow process in which a compressed gas is made to expand adiabatically irreversibly through a porous
plug and do work.
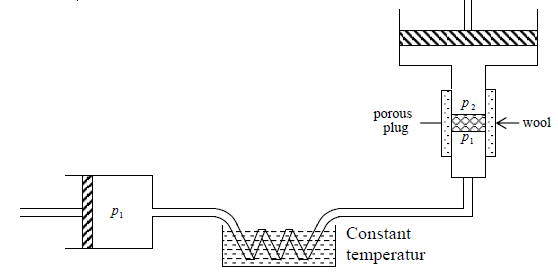
Fig: A schematic diagram of the porous-plug experiment for Joule-Kelvin
Let us assume that we start with a gas of internal energy U1 and volume V1 . After passing through the porous plug let final internal energy and volume of the gas be U2 and V2 respectively. No heat enters the system so this work has to performed at the expense of internal energy
Hence U1 + P1V1 = U2 + P2V2
H, = H2
Joule – Kelvin expansion is isenthalpic process
H = H(T,P)
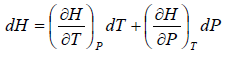
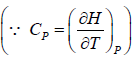
dH = 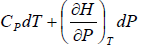
dH = TdS + VdP
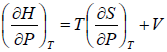
So dH = 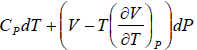
Since H does not change i.e. dH = 0 as the process is isoenthalpic the change in temperature w.r.t. pressure is given by
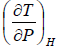 = μ =
= μ = 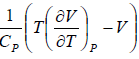 =
= 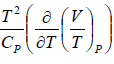
or μ = 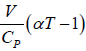
where μ is known as the Joule – Kelvin Coefficient.
This equation defines a curve in the (TP) plane and is known as the inversion curve when μ = 0 .
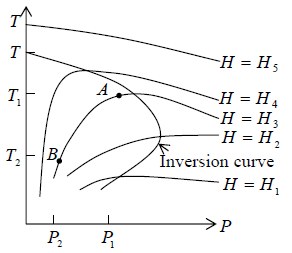
Figure: The inversion curve. Inside it the gas cools on undergoing Joule-Thomson expansion.
The temperature change ΔT = T1 - T2 produced in a series of isoenthalphs i.e. curve with H(T, P) = constant.
At T = Ti μ = 0 known as inversion temperature.
T < Ti μ = Positive . There is cooling effect of gases i.e. temperature and pressure move in same direction.
T > Ti μ = Negative . There is heating effect of gases i.e., temperature and pressure move in opposite direction.
Example 1: (a) For van der Waals gas prove that inversion temperature Ti = 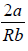 , where a and b are parameter used in van der Waals gas.
, where a and b are parameter used in van der Waals gas.
(b) Why Hydrogen and Helium shows heating effect as pressure increased at constant enthalphy.
(a) μ =
For van der Waals gas
⇒
Since, b << V
=
=
As,
μ =
For inversion temperature, μ = 0 ⇒
= b ⇒ Ti =
(b) Since inversion temperature of Hydrogen and Helium is very small. For cooling effect initial temperature must be smaller than inversion temperature but for Helium and Hydrogen inversion temperature is very small, so it is not possible to achieve initial temperature lower than inversion temperature, so Helium and Hydrogen give heated effect.
⇒
⇒
Phase Transition
A phase of a thermodynamic system and the state of matter has uniform physical properties.
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.
During a phase transition of a given medium certain properties of the medium changes often discontinuously as a result of some external condition such as temperature pressure and others.
Gibbs phase rule: It is proposed by Josiah Willard Gibbs which is given by
F = C - P + 2
Where C is number of components P is the number of phase in thermodynamic equilibrium with each other and F is number of degree of freedom.
Phase: A phase is form of matter that is homogeneous in chemical composition and physical state.
Typical phases are solid liquid and gas. Two immiscible (example-liquid mixture with different compositions) separated by distinct boundary are considered as two different phase.
Components: The number of components is the number of chemically independent constituents of the system i.e. minimum number of independent species necessary to define the composition of all phase of the system.
The number of degree of freedom (F) in the context is the number of intensive variable which are independent to each other.
First Order Phase Transition
Let us consider one component system in which system having only one kind of constituent particles. For first order phase transition, P - T diagram are shown in figure1.
Depending on the system at some values for temperature and pressure the three phases of the system may be found in equilibrium. In the P - T diagram the line OA represents equilibrium between solid and liquid phases the line OB represents equilibrium between solid and gas phases and the line OC represents equilibrium between liquid and gas phases. The point O where all the three phases are in equilibrium is known as a triple point. The line OC terminates at the point called the critical point. Beyond this point the gas phase cannot be converted into the liquid phase. In figure 1 the point C is at the apex of the P - T curve at the critical temperature Tc . For the temperature T > Tc the gas phase of the matter cannot be converted into the liquid phase but for T < Tc the gas phase in general can be converted into the liquid phase.
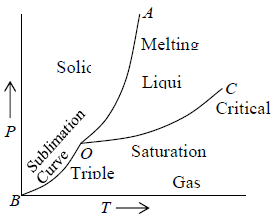
Figure 1: P-T phase of one component
Equilibrium between Two Phases
Let us consider an isolated system having a matter which is existing in two phases denoted by 1 and 2 simultaneously in equilibrium with each other (Figure 2). Suppose V1 and V2 are volumes N1 and N2 the number of particles E1 and E2 the internal energies, S1 and S2 the entropies of the two phases respectively. For each phase entropy is a function of its volume number of particles (mass) and internal energy.
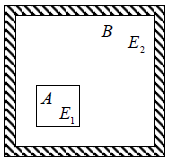
Figure 2: Equilibrium of two phases of an isolated one component system From these relations it follows that
From these relations it follows that
P1 = P2 (mechanical equilibrium)
μ1 = μ2 (chemical equilibrium)
Hence when two different phases of the matter are in equilibrium their temperatures pressures and chemical potentials must be equal. If the chemical potentials are expressed as function of pressure and temperature we have
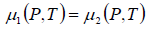
where P = P1 = P2 and T = T1 = T2 are the common pressure and temperature respectively of the two phases in equilibrium. Thus from above equation we have
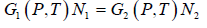
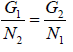
where G1(P, T) and G2(P, T) are the Gibbs free energies and N1 and N2 the number of particles in the two phases respectively. Since during the phase transition the number of
particles is not changing (i.e. N1 = N2) we have
G1(P, T) = G2(P, T)
Hence during the phase transition the Gibbs free energy does not change. Gibbs energies G1 and G2 of the two phases 1 and 2, respectively can be exhibited as shown in figure 3.
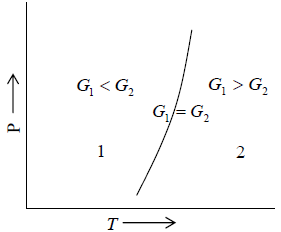
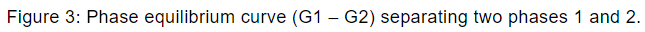
Clausius-Clapeyron equation
When the two phases denoted by 1 and 2 of the given matter are in equilibrium we have
G1(P, T) = G2(P, T)
where G1 and G2 are Gibbs free energies of the two phases respectively and P = P1 = P2 and T = T1 = T2 are the common pressure and temperature respectively of the two phases.
In the P - T diagram along the phase-transition line let us consider a point where the
pressure is P + dP and the temperature is T + dT, so that we have
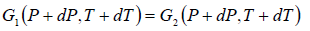
Using Taylor series expansion and neglecting the higher order terms we have
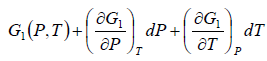 =
= 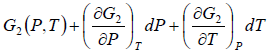
Using above two equation we get,
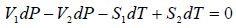
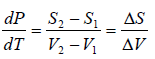
ΔS = 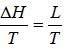
where ΔH(= H2 - H1) is the change in heat (enthalpy) which is the molar latent heat L.
Thus from above equation we have,
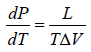
for V2 > V1, we have

further for S2 > S1 we have

Liquid-Vapour Phase Transition
Let us consider a phase transition from a liquid state to a vapour state. If Vl and Vg respectively denote the volume in the liquid and gases phases and Lv is the heat of vaporization (latent heat for the transition from liquid to vapour) the Clausius-Clapeyro equation is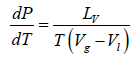
Since, in the phase transition Vg is always greater than Vl and the heat of vaporization Lv is positive, hence we have
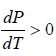
It shows that the boiling point of a liquid increases with the increase in pressure.
Now if the vapour pressure is low i.e. Vg >> Vl in comparison to Vg , then we have

Using the ideal gas equation g PVg = RT we have
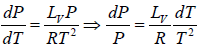
∴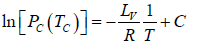
where C is a constant of integration. At the critical point we have P = Pc , T = Tc and equation is
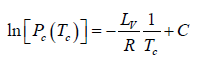
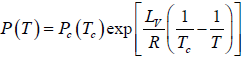
Here we have assumed that the heat of vapourisation Lv is independent of the temperature. However it depends on the temperature. Suppose it varies as Lv = a - bT then for an ideal gas at low pressure we have
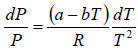
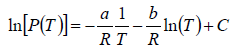
where C is a constant of integration. At the critical point we have P = Pc , T = Tc and equation is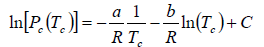
On putting the value of C , we have
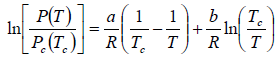
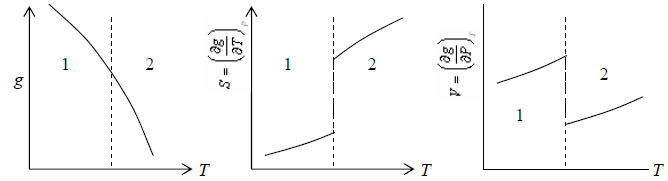
Properties of First Order Phase Transition
(1) Gibbs free energy is continuous
(2) First order derivative with respect to temperature and pressure have finite discontinuity i.e. entropy (S) and pressures (P) have finite discontinuity.
(3) Second and more higher order differential is infinite
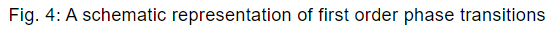
Example 2: For a two phase system in equilibrium, P is a function of T only so that
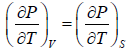 , show that
, show that
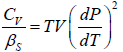
Let us take T and V as independent variables and write
S = S(T, V)
so that
For an adiabatic process it yields
Using first Maxwell relation we obtain
Since,
, so we can write
=
=
=
where, βs is adiabatic compressibility.
Example 3: Calculate under what Pressure water would boil at 120oC . One gram of steam occupies a volume of 1677 cm3 . Latent heat of steam = 540 cal / g j = 4.2 x107erg / cal, atmospheric pressure = 1.0x106 dyne / cm3
V2 = 1677cm3 / g V1 = 1cm3 / g
L = 4.2 x107 x 540erg / g, dT = 20o K
dP = 0.688 x 106 ⇒ P2 - P1 = 0.688 x 106 dyne / cm3
P2 = 0.688 x 106 + P1 = 1.688 x 106 dyne / cm3
Example 4: Liquid helium - 4 has normal boiling point of 4.2 K . However at pressure of 1 mm of mercury, it boils at 1.2 K. Estimate the average latent heat of vaporization of helium in this temperature range.
∴
⇒
⇒
Now, and , P0 = 760 mm and T0 = 4.2K, P = 1mm and T0 = 1.2K
⇒ L = 93.49 J /mol
Example 5: Liquid helium boils at temperature T0 when its vapour pressure is equal to P0, we now pump on the vapour and reduce the pressure to much smaller value P. Assume that the Latent heat L is approximately independent of temperature and helium vapour density is much smaller than that of liquid calculate the approximate temperature Tm of the liquid in equilibrium with its vapour at pressure P.
Express your answer in terms of L,T0,P0,Pm and any other required constants.
, where
∴ Tm =
Example 6: In the phase transition from a liquid state to a vapour state. The heat of vapourisation Lv varies with temperature T as 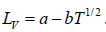 . Considering the gas as an ideal one at low pressure show that the pressure P(T) at temperature T in terms of the critical pressure Pc(Tc) at critical temperature Tc is given by
. Considering the gas as an ideal one at low pressure show that the pressure P(T) at temperature T in terms of the critical pressure Pc(Tc) at critical temperature Tc is given by
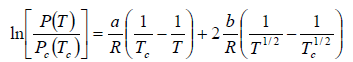
Clausius-Clapeyron equation for the phase transition from liquid to vapour is
where Lv is the heat of vapourisation and Vl and Vg, respectively denote the volume of liquid and gas phase. For low pressure Vg >> Vl
Using
, we have
For an ideal gas equation PVg = RT, and thus
At critical point, pressure and temperature are Pc and Tc, respectively.
From (i) and (ii), we have
Derive Clausius-Clapeyron equation from Maxwell relation,
⇒
⇒
∂Q = Ldm
Second Order Phase Transition
In some cases the state of matter does not change but the arrangement of its constituent particle changes. This kind of phase transition is known as second order phase transition.
In the case of second order phase transition no heat is evolved or absorbed. In second order phase transition-
1. Gibbs free energy is continuous
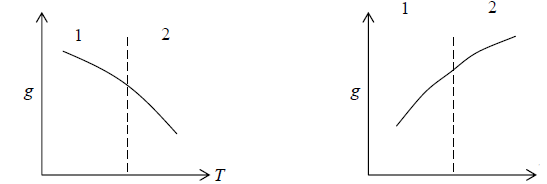
2. First order differential of Gibbs energy with respect to temperature ie entropy are changes smoothly
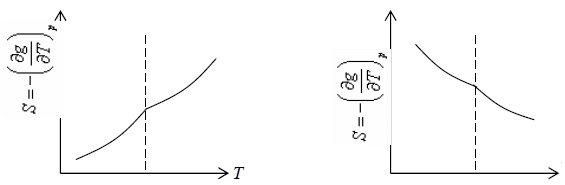
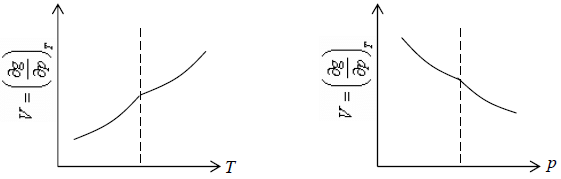
3. Second order differential of Gibbs energy with respect to temperature i.e., specific heat and second order differential of Gibbs energy with respect to pressure i.e. isothermal and isobaric expansivity have finite discontinuity at critical temperature.
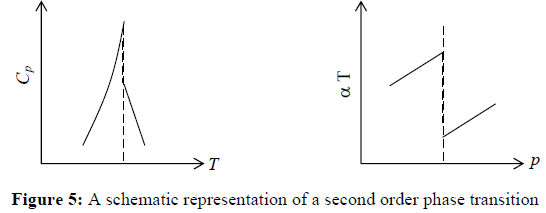
4. The thermodynamic properties which are determined by more than second order derivative will be infinite at critical temperature
|
6 videos|20 docs|32 tests
|
FAQs on Phase Transition & Low Temperature Physics - Kinetic Theory & Thermodynamics
| 1. What is the Third Law of Thermodynamics? |  |
| 2. How is low temperature production achieved by the Joule-Kelvin expansion? |  |
| 3. What is a phase transition? |  |
| 4. What is a second order phase transition? |  |
| 5. How is phase transition related to low temperature physics? |  |

|
Explore Courses for Physics exam
|

|

 ⇒
⇒ 

 =
=  =
= 


 = b ⇒ Ti =
= b ⇒ Ti = 
 ⇒
⇒ 
 ⇒
⇒ 




 , so we can write
, so we can write =
= 
 =
= 




 ⇒
⇒ 
 , where
, where 




 , we have
, we have






 ⇒
⇒  ⇒
⇒ 


















