Fractions Class 5 Notes Maths
What is a Fraction?
A fraction is a part of a whole. If a whole is divided into equal parts, each part is called a fraction. It is made up of two parts.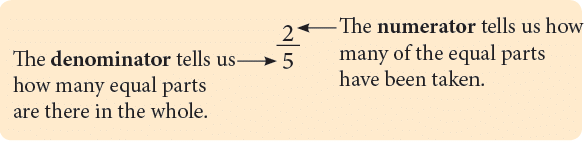
Fractions can be used to
- name a part of a single thing.
 Here, 1 part out of 4 equal parts is red, we write it as 1 / 4.
Here, 1 part out of 4 equal parts is red, we write it as 1 / 4. 1 / 4 of the cake has been taken by Neha.
1 / 4 of the cake has been taken by Neha. - name a part of a group of things.
 In this aquarium, you have 7 fish, out of which 2 are starfish. So, we write 2 / 7 are starfish.
In this aquarium, you have 7 fish, out of which 2 are starfish. So, we write 2 / 7 are starfish.
Representation of a Fraction on a Number Line
The fraction 3 / 8 is shown on the number line as: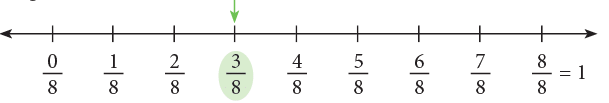 3 / 8 < 1, so we draw the number line from 0 to 1 and divide it into 8 equal parts. (∵ denominator = 8). The arrow shows the fraction 3 / 8.
3 / 8 < 1, so we draw the number line from 0 to 1 and divide it into 8 equal parts. (∵ denominator = 8). The arrow shows the fraction 3 / 8.
Types of Fractions
- Proper Fractions
The fractions in which the numerator is less than the denominator are called proper fractions.
For example, 0 / 2, 1 / 4, 2 / 5, 3 / 7, 81 / 100, etc., are all proper fractions. All proper fractions are less than 1. - Improper Fractions
The fractions in which the numerator is greater than or equal to the denominator are called improper fractions.
For example, 6 / 6, 7 / 4, 21 / 20, 121 / 100, etc., are all improper fractions.
All improper fractions are greater than or equal to 1. (i) Mixed Numbers
(i) Mixed Numbers
A mixed number has two parts, a whole number part (except 0) and a part with a fraction.
For example, are all mixed numbers.
are all mixed numbers.
- Unit Fractions
A fraction whose numerator is 1 and the denominator is greater than 1 is called a unit fraction,
For example, 1 / 8, 1 / 3, 1 / 5, etc. - Like Fractions
Fractions that have the same denominator are called like fractions.
For example, 8 / 12, 7 / 12, 17 / 12, 23 / 12 are all like fractions. - Unlike Fractions
Fractions whose denominators are different are called unlike fractions.
For example, 4 / 6, 3 / 8, 12 / 15, 23 / 35 are all unlike fractions.
Edurev Tips: We can write a mixed number as an improper fraction and an improper fraction as a mixed number.
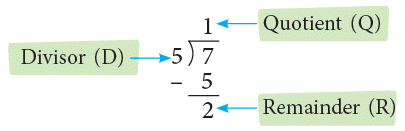
Example 1: Write 7 / 5 as a mixed number.
Method 1: Pictorially, it can be shown as:
It can also be represented on the number line as:Jump five-fifths to land on 1. Jump 2 more fifths to land on 7 / 5.
This is same as jumping to 1 and then to another 2 / 5.
∴ 7 / 5 as a mixed number is
Method 2: By Division Method,
Edurev Tips:
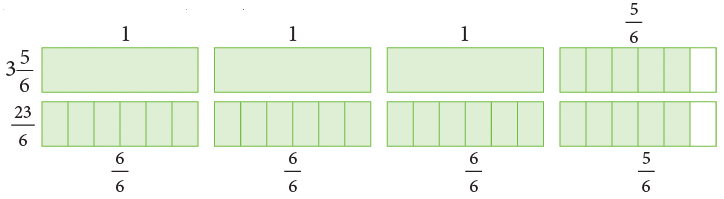
Example 2: Write 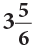 as an improper fraction.
as an improper fraction.
Pictorially, it can be shown as:
Multiply the whole number part by the denominator and add numerator to the product.
Alternatively,
Equivalent Fractions
Consider the following fraction bars.
Fractions that name the same part of the whole are called equivalent fractions.
Therefore, 1 / 4, 2 / 8 and 3 / 12 are equivalent fractions and we write 1 / 4 = 2 / 8 = 3 / 12.
Edurev Tips:
Thus, to find equivalent fractions, we either multiply or divide the numerator and denominator by the same number.
Example 3: Fill in the missing numbers.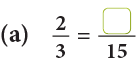
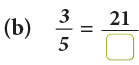
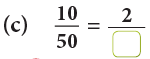
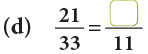
Writing a Fraction in its Simplest Form
A fraction is in its simplest form when its numerator and denominator have no common factors other than 1.
Fractions such as 1 / 2, 3 / 5, 5 / 8 are all fractions in their simplest form. In 1 / 2, there is no common factor of 1 and 2 except 1. Likewise, the only common factor of 3 and 5 in 3 / 5 is 1 and of 5 and 8 in 5 / 8 is 1.
The fraction 10 / 15 is not in its simplest form because 5 is a common factor of 10 and 15.
Similarly, 3 / 21 is not in its simplest form because 3 is a common factor of both 3 and 21.
Example 4: Express the following fractions in their simplest form.
(a) 6 / 8
(b) 15 / 30
(c) 210 / 330
(a) Divide both numerator and denominator by a common factor.
Dividing 6 and 8 by 2, we have,
(b)
Hence, 15 / 30 in its simplest form = 1 / 2, because 1 and 2 have no common factor except 1.
Alternative Method:
Method: To reduce a fraction to its simplest form, keep dividing by common factors until the only common factor is 1.
(c)
Comparing Fractions
1. Comparing Fractions with Like Denominators
Example 5: For a singing competition, 6 / 15 of the children are girls and 9 / 15 are boys. Whose number is greater in the competition, of boys or of girls?
To answer this question we have to compare 6 / 15 and 9 / 15. We can use two ways for comparing them and then state a general rule.
Method 1: Comparing PictoriallyOn comparing the shaded parts, you can see that 9 / 15 > 6 / 15.
∴ The number of boys is more.
Method 2: Comparing on Number Line9 / 15 is to the right of 6 / 15, therefore, 9 / 15 > 6 / 15.
Rule: If two or more fractions have the same denominator, the fraction with the greater numerator is the greater number, e.g., 6 / 7 > 5 / 7 or 5 / 7 < 6 / 7.
2. Comparing Fractions with Unlike Denominators
Example 6: Which is greater: 1 / 3 or 2 / 5?
Pictorially, 1 / 3 and 2 / 5 can be compared as:
Method 1On comparing the shaded parts, you can see that 2 / 5 > 1 / 3.
Method 2Comparing fractions on number line, you can see that 2 / 5 is on the right of 1 / 3.
3. By Finding Equivalent Fractions Using LCM
To compare 1 / 3 and 2 / 5, we convert them into equivalent fractions both having the same denominator.
The common denominator in this case will be taken as the LCM of 3 and 5.
LCM of 3 and 5 = 3 × 5 = 15.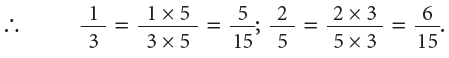
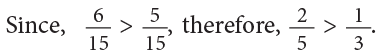
Edurev Tips: This is the most commonly used method for comparing and ordering unlike fractions.
Ordering Fractions
Now that you know how to compare fractions, you can order them in any order— increasing or decreasing.
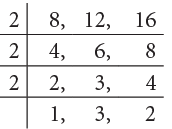
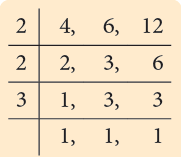
Example 7: Arrange the fractions 7 / 8, 5 / 12, 15 / 16 in increasing order.
Step 1: Find the LCM of the denominators 8, 12 and 16.
LCM of 8, 12 and 16 = 2 × 2 × 2 × 3 × 2 = 48
Step 2: Find the equivalent fractions with denominator 48.
Step 3: Compare the equivalent fractions:
Arranging the fractions in increasing order,
You can write the same fractions in decreasing order as
Ordering Unit Fractions
A unit fraction has 1 as its numerator, but the denominator can vary.
For example, 1 / 2, 1 / 3, 1 / 4, 1 / 5 are unit fractions. What conclusion do you draw from the following diagrams?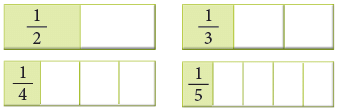 It can be clearly seen that
It can be clearly seen that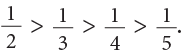
Thus, if the numerator is the same, the fraction with the least denominator is the greatest.
Addition and Subtraction of Fractions
1. To Add or Subtract Like Fractions (Fractions with the Same Denominator)
When we add or subtract fractions with the same denominator, we just add or subtract the numerators and keep the denominator same.
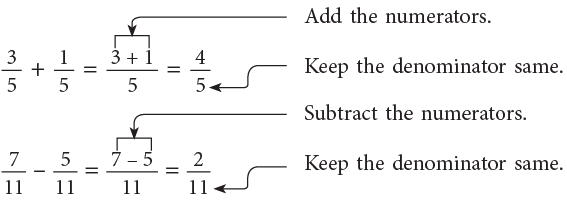
2. To Add or Subtract Unlike Fractions
Example 8: Ravi and Nisha are painting a wall. Ravi painted 1 / 2 of the wall and Nisha painted 1 / 4 of the wall. What part of the wall did they paint altogether?
Wall painted by Ravi = 1 / 2
Wall painted by Nisha = 1 / 4
Total part of the wall painted = 1 / 4 + 1 / 2
To be able to add these, first change one or both of the fractions to fractions having common denominator.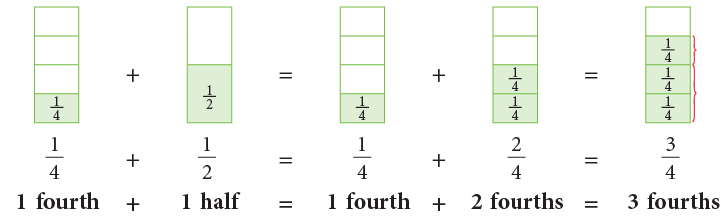
Therefore, 3 / 4 part of the wall was painted by Ravi and Nisha.
Rule: When we add fractions with different denominators, we change the fractions to fractions having the same denominator. This common denominator is the least common denominator of the given fractions.
What is meant by least common denominator?
Study the two rows of fractions given below: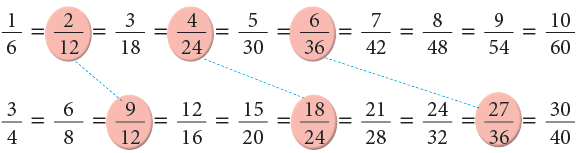 The numbers 12, 24 and 36 are some of the common denominators of 1 6 and 34. Of these, 12 is the least common denominator. Also, we can see that 12 is the LCM of 6 and 4. Thus, the least common denominator of two fractions is the same as the least common multiple of their denominators.
The numbers 12, 24 and 36 are some of the common denominators of 1 6 and 34. Of these, 12 is the least common denominator. Also, we can see that 12 is the LCM of 6 and 4. Thus, the least common denominator of two fractions is the same as the least common multiple of their denominators.
To add or subtract unlike fractions, write the given fractions as equivalent fractions with the least common denominator (LCM of the denominators) and then add or subtract like fractions.
Example 9: Add: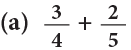
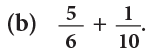
Method 1: LCM of 4 and 5 = 4 × 5 = 20Method 2: You may also set your work as under:
Step 1: LCM of 4 and 5 = 20
Step 2: Divide 20 by the denominator of the first fraction. 20 ÷ 4 = 5
Multiply quotient 5 by numerator 3 and write 3 × 5.
Divide 20 by the denominator of the second fraction. 20 ÷ 5 = 4
Multiply quotient 4 by numerator 2 and write 2 × 4.
Now, complete as shown.
LCM of 6 and 10 = 30.
Changing 5 / 6 and 1 / 10 to equivalent fractions having the same denominator 30.
Example 10: Subtract: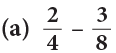
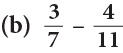
Method 1
LCM of 8 and 4 = 8.
Method 2
LCM of 7 and 11 is 7 × 11 = 77.
Addition of Mixed Fractions
Type I: With Same Denominators
Example 11: When released, a gas balloon first rose by 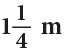 and then again by
and then again by
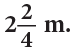 What is the total height to which the gas balloon rose?
What is the total height to which the gas balloon rose?
Pictorially, the problem can be represented as:
Thus, we can add mixed numbers by first adding whole numbers and then proper fractions. Therefore, the above work can be set as:
Example 12: A cow gave 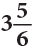 litres of milk in the morning and
litres of milk in the morning and 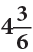 litres in the evening. Find the total quantity of the milk given by the cow.
litres in the evening. Find the total quantity of the milk given by the cow.
Method 1
Method 2
Total quantity of milk given by the cow
Convert each mixed number to improper fraction.
∴ So, the cow gavelitres of milk in all.
Type II: With Different Denominators
Example 13: Add: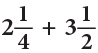
Method 1
LCM of 2 and 4 = 4.
Method 2
By changing into improper fractions
Example 14: Add: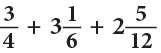
Method 1
LCM of 4, 6, 12 = 2 × 2 × 3 = 12.
Method 2
Edurev Tips: Method 1 is particularly useful when the whole number parts of given fraction are large numbers such as in
Subtraction of Mixed Fractions
Example 15: Subtract: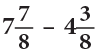
Example 16: Subtract
Method 1
Step 1: Subtract the whole numbers.
Step 2: Change fractions to equivalent fractions, 1 / 4 = 3 / 12.
Step 3: Subtract the fractions.
Method 2
Convert mixed fractions into improper fractions.
Subtracting from Whole Numbers
Subtracting from 1
Example 17: Mira is preparing a sweet dish. She used 5 / 8 litre of milk from a jug containing 1 litre milk. How much milk is left in the jug?
Quantity of milk remaining in jug
Or
Mira still has 3 / 8 litre of milk left in the jug.
Example 18: David lives 3 kilometres away from a town. Paul lives 56 of a kilometre away from the town. How much closer does Paul live to the town than David?
Method 1
Paul lives
Thus, Paul liveskm closer to the town as compared to David.
Method 2
Paul liveskm closer.
Thus, Paul liveskm closer to the town as compared to David.
Edurev Tips: In subtraction sums like
where whole number parts are large numbers, it may be easier and more convenient to apply method 1.
Thus,
Example 19: Subtract: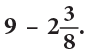
Method 1
Method 2
Method 2 is generally preferred.
Properties of Addition of Fractions
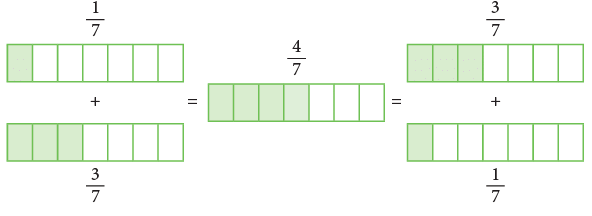
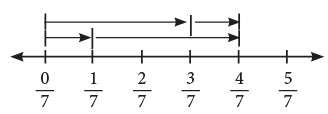
- Changing the order of two addends does not change the sum.

Pictorially, it can be shown as:
 Similarly, by actual addition, you can verify that;
Similarly, by actual addition, you can verify that;

- Changing the way in which we group the addends does not change the sum.



Thus,
Or


This is called the grouping property of addition of fractions. - Additive property of 0.

Thus, the sum of a fraction and 0 is the fraction itself.
Problems Based on Real Life Situations
Example 20: Deepa used 5 / 9 L of milk to prepare kheer. She added 1 / 2 L more milk to the kheer. How many litres of milk did she use to make the kheer?
Milk used by Deepa = 5 / 9 L
Milk added by her = 1 / 2 L
Total quantity of milk used (in litres)= (5 / 9 + 1 / 2)
LCM of 9 and 2 is 18.
∴ Deepa usedof milk for the kheer.
Example 21: Pinki had 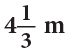 of a ribbon. She used
of a ribbon. She used 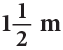 of the ribbon to wrap some gifts. How much ribbon is left with her?
of the ribbon to wrap some gifts. How much ribbon is left with her?
Ribbon with Pinki
Ribbon used
Ribbon left (in metres)
LCM of 2 and 3 is 6.
Thus, Pinki hadof ribbon left with her.
|
32 videos|57 docs|45 tests
|
FAQs on Fractions Class 5 Notes Maths
| 1. What is a fraction? |  |
| 2. How do you find equivalent fractions? |  |
| 3. How do you write a fraction in its simplest form? |  |
| 4. How do you compare fractions? |  |
| 5. How do you order fractions? |  |

|
Explore Courses for Class 5 exam
|

|
 Here, 1 part out of 4 equal parts is red, we write it as 1 / 4.
Here, 1 part out of 4 equal parts is red, we write it as 1 / 4.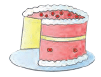 1 / 4 of the cake has been taken by Neha.
1 / 4 of the cake has been taken by Neha.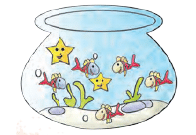 In this aquarium, you have 7 fish, out of which 2 are starfish. So, we write 2 / 7 are starfish.
In this aquarium, you have 7 fish, out of which 2 are starfish. So, we write 2 / 7 are starfish. (i) Mixed Numbers
(i) Mixed Numbers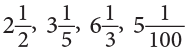 are all mixed numbers.
are all mixed numbers.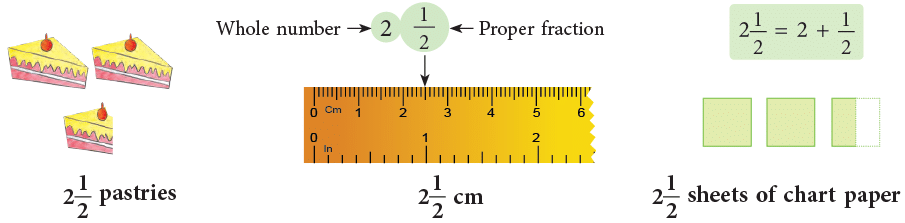
 Jump five-fifths to land on 1. Jump 2 more fifths to land on 7 / 5.
Jump five-fifths to land on 1. Jump 2 more fifths to land on 7 / 5.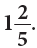
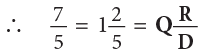

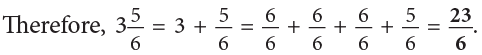
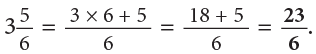
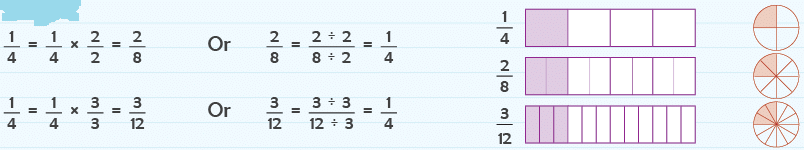
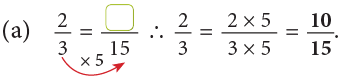
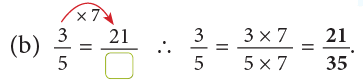
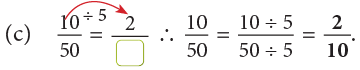
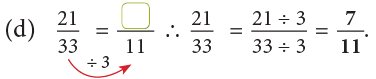




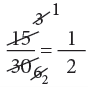
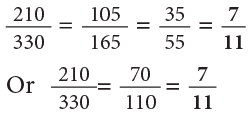

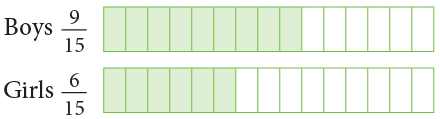 On comparing the shaded parts, you can see that 9 / 15 > 6 / 15.
On comparing the shaded parts, you can see that 9 / 15 > 6 / 15.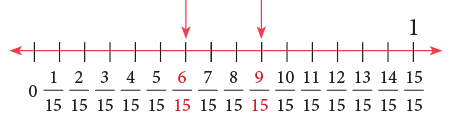 9 / 15 is to the right of 6 / 15, therefore, 9 / 15 > 6 / 15.
9 / 15 is to the right of 6 / 15, therefore, 9 / 15 > 6 / 15.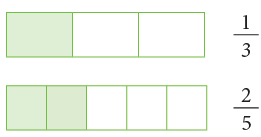 On comparing the shaded parts, you can see that 2 / 5 > 1 / 3.
On comparing the shaded parts, you can see that 2 / 5 > 1 / 3.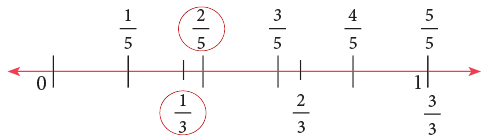 Comparing fractions on number line, you can see that 2 / 5 is on the right of 1 / 3.
Comparing fractions on number line, you can see that 2 / 5 is on the right of 1 / 3.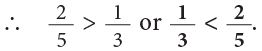
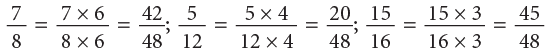
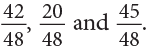
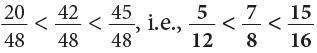
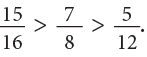
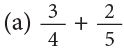
 Method 2: You may also set your work as under:
Method 2: You may also set your work as under: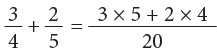
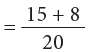
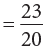
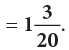
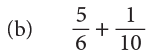
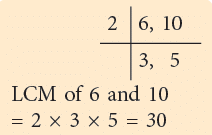
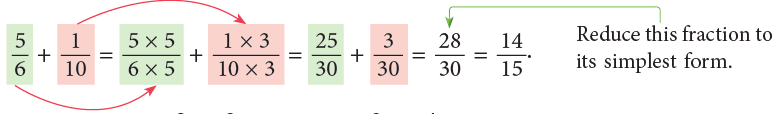
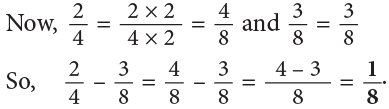
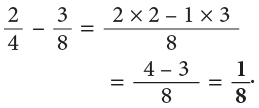
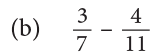
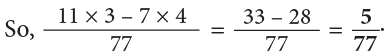
 Thus, we can add mixed numbers by first adding whole numbers and then proper fractions. Therefore, the above work can be set as:
Thus, we can add mixed numbers by first adding whole numbers and then proper fractions. Therefore, the above work can be set as: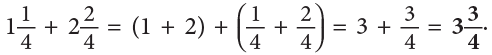
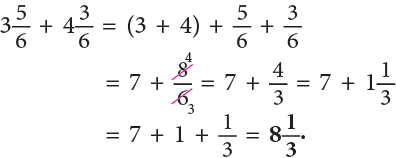
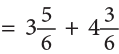
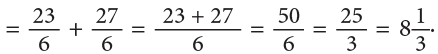
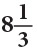 litres of milk in all.
litres of milk in all.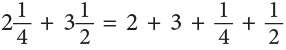
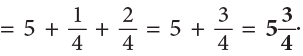
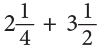
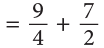
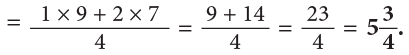
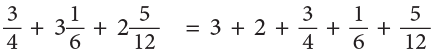
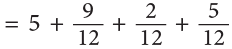
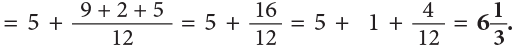
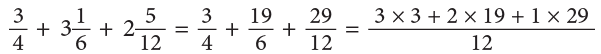
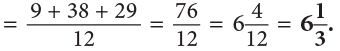
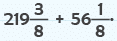
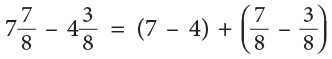
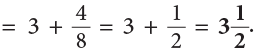
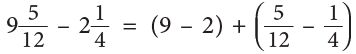
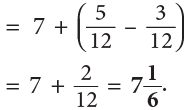
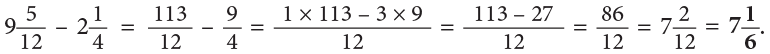
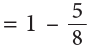
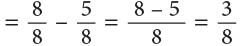
 km closer to the town as compared to David.
km closer to the town as compared to David.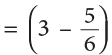 km closer.
km closer.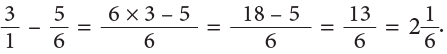
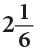 km closer to the town as compared to David.
km closer to the town as compared to David. where whole number parts are large numbers, it may be easier and more convenient to apply method 1.
where whole number parts are large numbers, it may be easier and more convenient to apply method 1.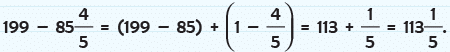
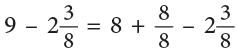
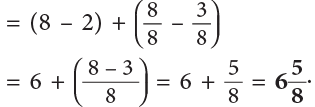
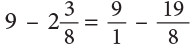
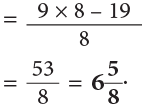
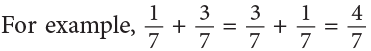
 Similarly, by actual addition, you can verify that;
Similarly, by actual addition, you can verify that;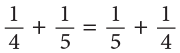
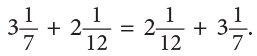
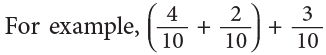
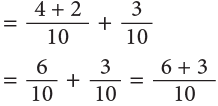
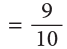
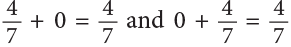
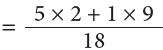
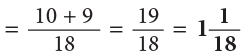
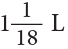 of milk for the kheer.
of milk for the kheer.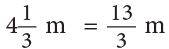
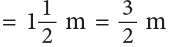
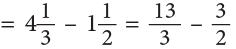
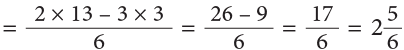
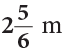 of ribbon left with her.
of ribbon left with her.












