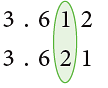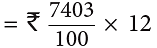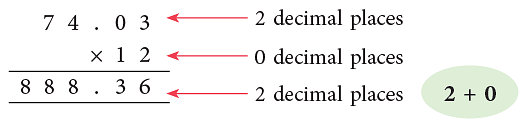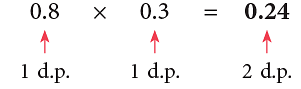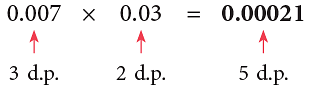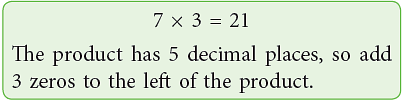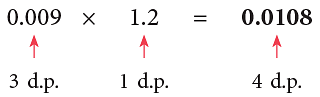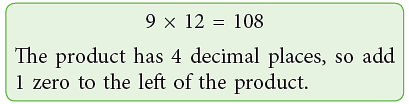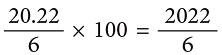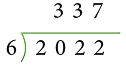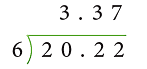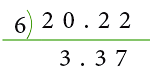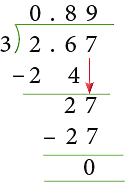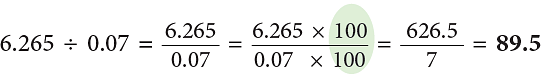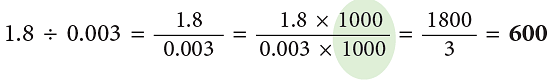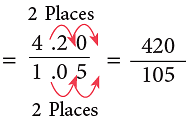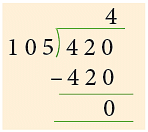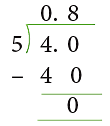Decimals Class 5 Notes Maths
Let’s dive into an exciting world of decimals, where we learn how to represent parts of a whole and explore how these numbers make life easier!
- Have you ever wondered how shopkeepers weigh lentils to be 1.5 kg ?
- Or how a length of 2.5 meters is written?
That’s exactly where decimals come into play!
Decimals
- A decimal is a number that represents parts of a whole.
- It contains two parts:
Whole part – The part before the decimal point (.)
Fractional part – The part after the decimal point. - For example:
Think of a pizza having 10 parts in total.
If we eat 3 parts, we will be left with 7/10 parts
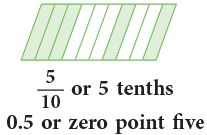
1. Tenths
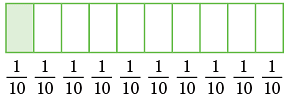
- The fraction 1 / 10, as a decimal, is written as 0.1 and read as zero point one.
- The following shaded parts can be read as:


The dot or the point between the two digits is called the decimal point.
- Whole numbers and decimal numbers can also be combined as shown below:
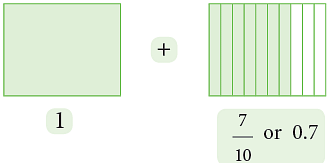
- The picture given alongside shows, on a ruler, a length of 1 cm + 7 parts out of 1 cm.
- Since each cm is further divided into 10 equal parts (as can be seen), the above given number can be written as 1.7.

- 1.7 is also a decimal number and is read as one point seven.

2. Hundredths
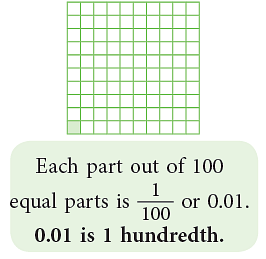
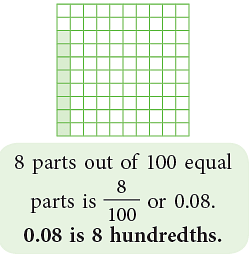
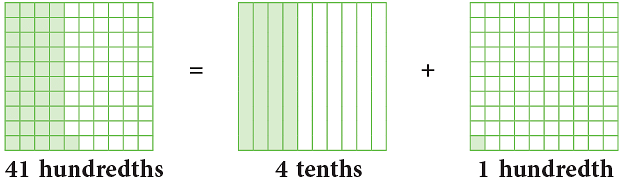
- Let us now divide a whole into 100 equal parts.
- The following shaded parts can be read as

- 0.41 is 41 hundredths or 4 tenths 1 hundredth.


- Similarly,


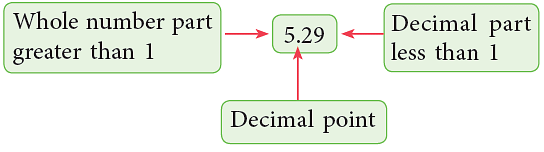
- So, a decimal number has two parts—the whole number part and the decimal part separated by a decimal point. Number of digits after the decimal point is called the number of decimal places.
 In the above number, there are 2 decimal places after the whole number part.
In the above number, there are 2 decimal places after the whole number part.
Did You Know
We read
- 0.01 as zero point zero one,
- 0.08 as zero point zero eight,
- 0.75 as zero point seven five.
3. Thousandths
- If we divide one whole into thousand equal parts, then each part of the whole represents one-thousandth.
Thus, 1 / 1000 = 0.001 or one-thousandth read as zero point zero zero one. - The decimal 0.716 = 716 / 1000 (716 thousandths) represents 716 parts out of 1000 parts.
- Sumit and Ritu are both reading the number 0.716 in different ways. Tick
 the correct one?
the correct one?
- In expanded form, we write 0.716 as:

- Similarly, 49.107 is forty-nine and one hundred seven thousandths and is read as forty-nine point one zero seven.
In expanded form,
- Notice the following pattern.

EduRev Tip:
The number of digits after the decimal point in the decimal numeral is equal to the number of zeros after 1 in the denominator of the corresponding common fraction.
Place Value and Decimals
The place value chart shown below can also be used to understand decimals. The place value of each digit in the number 2222.222 is shown below.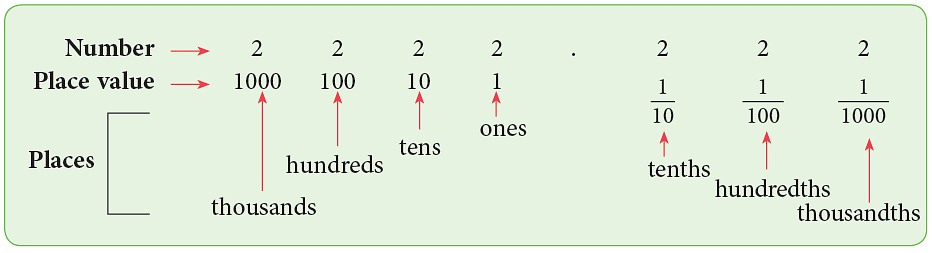 The first place to the right of the decimal point is the tenths place, the second place to the right is the hundredths place and so on.
The first place to the right of the decimal point is the tenths place, the second place to the right is the hundredths place and so on.
The last place after the decimal point tells us how to name the decimal part.
EduRev Tips: Digit at each place has a place value i sone-tenth (1 / 10) to that of the place to its left.
Converting Fractions to Decimals and Vice versa
1. Converting Fractions to Decimal
- Fractions whose denominators are 10, 100 or 1000 can be easily converted to decimals by putting the decimal point in the numerator accordingly.
Examples:
1.

2.

- For fractions which can be converted to equivalent fractions having denominators 10 or multiples of 10, we apply the same method as above.

- Similarly,


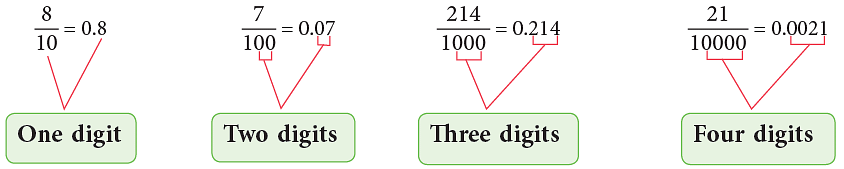
2. Converting Decimals to Fractions
- Decimals can also be converted into fractions as under
 Pictorial representation of how to convert a decimal to a fraction
Pictorial representation of how to convert a decimal to a fraction
Equivalent Decimals
- Decimals that name the same amount are called equivalent decimals.
- Observe the following.
 As can be seen, these two pictures name the same amount, so 0.8 = 0.80.
As can be seen, these two pictures name the same amount, so 0.8 = 0.80.
8 tenths = 80 hundredths
8 / 10 = 80 / 100
Thus, 0.8 = 0.80 = 0.800 = 0.8000 = ______
Similarly, 1.8 = 1.80 = 1.800 ; 37.41 = 37.410 = 37.4100, etc. - From the above it is clear that writing zeros at the right hand end of a decimal number does not change its value.
Like Decimals and Unlike Decimals
- Decimals having the same number of decimal places are called like decimals.

- Decimals having different number of decimal places are called unlike decimals.
Thus, 1.2, 4.03, 0.895 are all unlike decimals.
Converting Unlike Decimals to Like Decimals
Unlike decimals can be converted to like decimals by finding their equivalent decimals.
Example: Convert 6.8, 7.83 and 12.040 to like decimals.
The greatest number of decimal places is 3, so we convert all of them to equivalent decimals with 3 decimal places.
6.8 → 6.800, 7.83 → 7.830, 12.040
Hence, 6.8, 7.83 and 12.040 when converted to like decimals becomes 6.800, 7.830, 12.040.
Comparing and Ordering Decimals
1. Comparing Decimals
To compare decimal numbers, we follow the following steps.
Step 1: Convert the decimals into like decimals.
Step 2: First, compare the whole number parts. The number with the greater whole number part is greater.
Step 3: If the whole number parts are the same, compare the tenths digits. The decimal number having greater tenths digit names a greater number.
Step 4: If the tenths digits are the same, compare the hundredths digits and so on.
Example : Which number is bigger: 3.612 or 3.621?
The numbers are
On comparing the digits from the left, you find that the hundredths digits differ.
Since 2 hundredths > 1 hundredths, therefore, 3.621 > 3.612.
2. Ordering Decimals
Example: Arrange 21.012, 21.002, 24.102 in increasing order.
Sol: On comparing the whole number parts, you find that 24.102 is the greatest.
Now, compare 210.12 and 21.002.
The whole number parts being the same, we start comparing from the tenths digit.
The digits at the hundredths differ. Since 1 hundredths > 0 hundredth, so 21.012 > 21.002.
Thus, the given numbers in increasing order are: 21.002, 21.012, 24.102.
Addition and Subtraction of Decimals
1. Addition
To add two or more decimals, we follow these steps.
Step 1: Convert the decimal to like decimals.
Step 2: Line up the decimal points, i.e., the addends are placed one below the other such that the tens digit is below tens, ones is below ones, decimal points below the decimal point, tenths below the tenths and so on.
Step 3: Add, as in case of whole numbers. Carry wherever necessary.
Step 4: Place the decimal point in the sum directly below the decimal point in the addends.
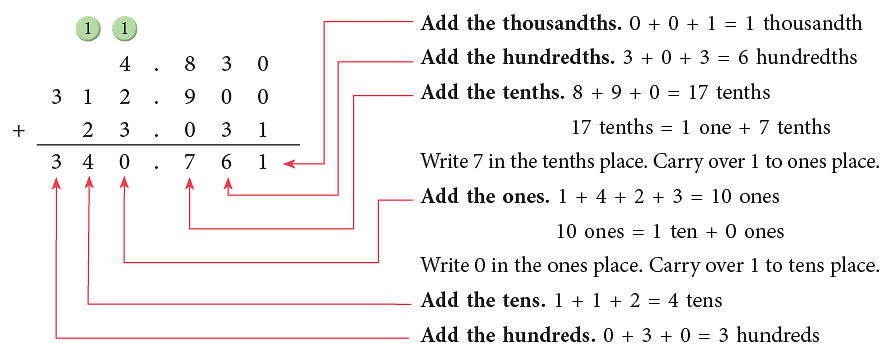
Example: Add: 4.83, 312.9 and 23.031.
First, we convert the numbers to be added to like decimals.
We have: 4.83 → 4.830, 312.9 → 312.900, 23.031.
Now, line up the decimals and add.
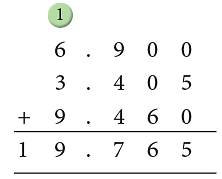
Example: Add: 6.9, 3.405 and 9.46.
First, we convert the numbers to be added to like decimals.
Converting into like decimals 6.9 → 6.900, 3.405, 9.46 → 9.460.
Now, line up the decimals and add.
EduRev Tips:
A whole number can be expressed in the decimal form as: 12 = 12.0 or 12.00 or 12.000 and so on.
2. Subtraction
To subtract one decimal number from the other, we follow the steps given below.
Step 1: Convert the decimal to like decimals.
Step 2: Line up the decimal points.
Step 3: Subtract in each place value.
Step 4: Regroup, wherever necessary.
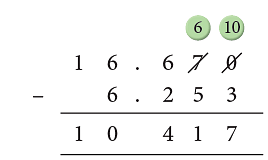
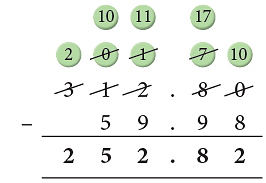
Example: Subtract 6.253 from 16.67.
- Convert into like decimals as 16.67 → 16.670, 6.253 and line up the decimal points.
- Subtract the thousandths.
You cannot subtract 3 thousandths from 0 thousandths, so borrow 1 hundredths from 7 hundredths leaving behind 6 hundredths.
1 hundredths = 10 thousandths
0 thousandths → 10 thousandths
Now, subtract thousandths, 10 – 3 = 7 thousandths.- Subtract the hundredths.
6 – 5 = 1 hundredth- Subtract the tenths.
6 – 2 = 4 tenths- Subtract the ones.
6 – 6 = 0 ones- Subtract the tens.
1 – 0 = 1 ten
So, 16.67 – 6.253 = 10.417.
Example: Find 312.8 – 59.98.
Multiplication of Decimals
1. Multiplication by 10, 100, 1000
Observe the following examples.
(i)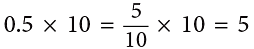
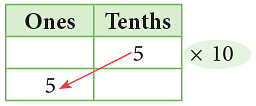
5 tenths × 10 = 5 ones
0.5 × 10 = 5
(ii) 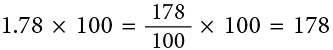
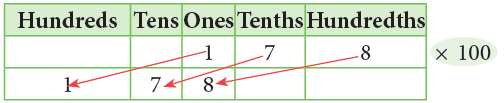
1 ones 7 tenths 8 hundredths × 100
= 1 hundreds 7 tens 8 ones
(iii) 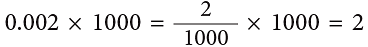

2 thousandths × 1000 = 2 on1 one 8 tenths = 1 thousand 8 hundreds
We observe that:
- Multiplying a decimal by 10 moves the decimal point 1 place to the right
Multiplying a decimal by 100 moves the decimal point 2 places to the right.
Multiplying a decimal by 1000 moves the decimal point 3 places to the right.
2. Multiplication by a Counting Number
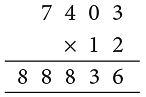
Example 1: If one litre of petrol costs ₹ 74.03, what will be the cost of 12 litres of petrol?
Cost of 12 L petrol = ₹ 74.03 × 12
Step 1: Multiply, as you would multiply counting numbers.
Step 2: Place the decimal point in the product at a place so that the number of decimal places in the product is equal to the total number of decimal places of the factors.
Example 2: Multiply 6.095 by 45.
3. Multiplication of a Decimal Number by a Decimal Number
Lets us find the product of 12.7 and 0.4.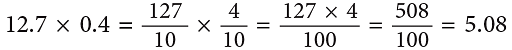
The above work can also be set as:
Working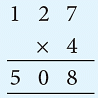
Multiply, as you would multiply the counting numbers.
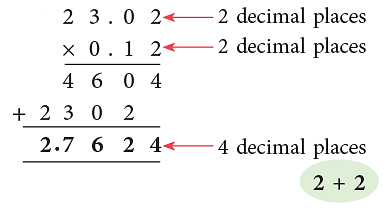
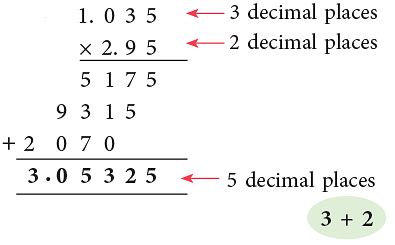
The total number of decimal places in the product is equal to the sum of the decimal places of the factors.
Example 1: Multiply:
(a) 0.8 × 0.3
(b) 0.007 × 0.03
(c) 0.009 × 1.2
(a)
(b)
(c)
Example 2: Multiply 23.02 by 0.12.
Example 3: Multiply 1.035 by 2.95.
Example 4: Multiply:
(a) 2.6 by 30
(b) 13.46 by 600
(a) 2.6 × 30 = 2.6 × 3 × 10 = 7.8 × 10 = 78.
(b) 13.46 × 600 = 13.46 × 6 × 100 = 80.76 × 100 = 8076.
Division of Decimals
1. Division by 10, 100, 1000
Observe the following examples.
(i) 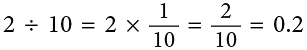
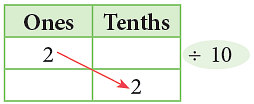
2 ones ÷ 10 = 2 tenths = 0.2
(ii) 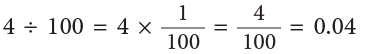
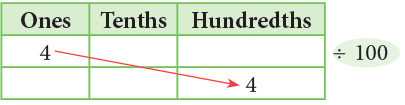
4 ones ÷ 100 = 4 hundredths = 0.04
(iii) 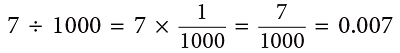
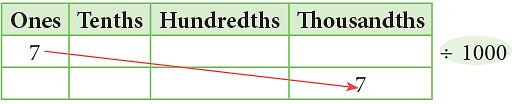
7 ones ÷ 1000 = 7 thousandths = 0.007
Did You Know
- Dividing a decimal by 10 moves the decimal point one place to the left.
- Dividing a decimal by 100 moves the decimal point 2 places to the left.
- Dividing a decimal by 1000 moves the decimal point 3 places to the left.
2. Division by a Counting Number
Example 1: Find: 20.22 ÷ 6.
Compare the two workings shown below.
Step 1:
1. 20.22 / 6
Step 2:
2.
Step 3:
3. 2022 / 6 = 337
Step 4:
4. 337 ÷ 100 = 3.37
Actual Working
Method:
1. Divide, as you would divide counting numbers.
2. Place the decimal point in the quotient directly above the decimal point in the dividend.
Short formSo, 20.22 ÷ 6 = 3.37
Example 2: Divide: 2.67 by 3.
3 > 2, so we put a zero in the quotient.
Check
3 × 0.89 = 2.67
∴ 2.67 ÷ 3 = 0.89.
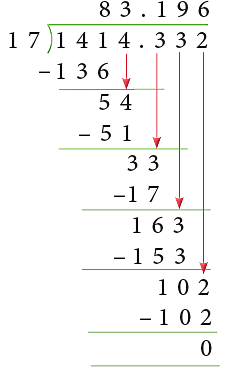
Example 3: Solve: 1414.332 ÷ 17.
∴ 1414.332 ÷ 17 = 83.196.
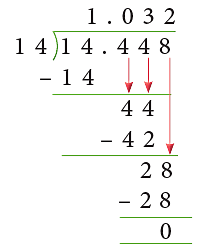
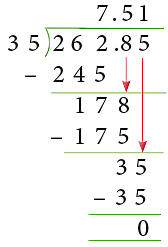
Example 4: Divide the following.
(a) 14.448 ÷ 14
(b) 262.85 ÷ 35
(a)
∴ 14.448 ÷ 14 = 1.032.
(b)
∴ 262.85 ÷ 35 = 7.51.
Check
35 × 7.51 = 262.85
If the last remainder is not zero, write as many zeros on the right of the dividend as are necessary to make the last remainder zero.
3. Division of a Decimal Number by a Decimal Number
You have learnt how to divide a decimal number by a whole number. To divide a decimal number by a decimal number, we make the divisor a whole number.
Look at the following example.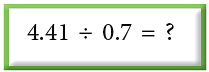
(i) Multiply the divisor by a multiple of 10 to make it a whole number.
Thus, 0.7 × 10 = 7.
(ii) Multiply the dividend by the same multiple of 10.
Thus, 4.41 × 10 = 44.1.
Now, divide as usual:
44.1 ÷ 7 = 44.1 / 7 = 6.3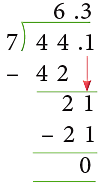
The work can be set as: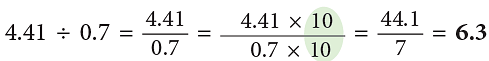
Example 1: Divide : (a) 6.265 ÷ 0.07 (b) 1.8 ÷ 0.003
(a)
(b)
Example 2: Divide: 4.20 by 1.05.
4.20 ÷ 1.05 = 4.20 / 1.05
2 decimal places in divisor, s o shif t de cima l p oint 2 places to the right both in divisor and dividend.
∴ 4.20 ÷ 1.05 = 4.
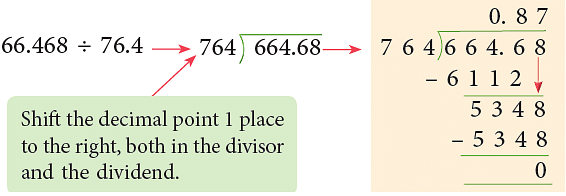
Example 3: Divide 66.468 by 76.4.
∴ 66.468 ÷ 76.4 = 0.87.
Example 4: Divide:
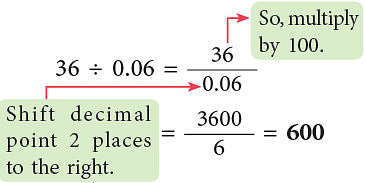
(a) 90 ÷ 0.60
(b) 36 ÷ 0.06
(a)
(b)
Changing Common Fractions to Decimal Fractions
Example 1: Change 4 / 5 to a decimal fraction.
To convert 4 / 5 to a decimal, we divide the numerator 4 by the denominator 5, as follows.
Put decimal point after the whole number and add 1 zero to ensure complete division.
∴ 4 / 5 = 0.8.
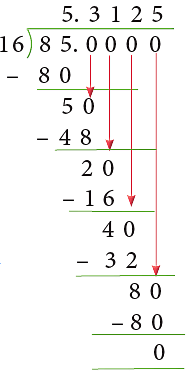
Example 2: Express 85 / 16 as a decimal.
To convert 85 / 16 to a decimal, divide the numerator 85 by the denominator 16.
Put decimal point after the whole number and add 4 zeros to ensure complete division.
∴ 85 / 16 = 5.3125.
|
32 videos|57 docs|45 tests
|
FAQs on Decimals Class 5 Notes Maths
| 1. What is the place value of digits in a decimal number? |  |
| 2. How do you convert a fraction to a decimal? |  |
| 3. What are equivalent decimals? |  |
| 4. How can I compare and order decimal numbers? |  |
| 5. How do you add and subtract decimal numbers? |  |

|
Explore Courses for Class 5 exam
|

|
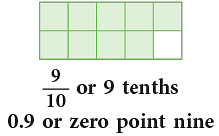
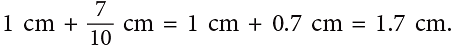
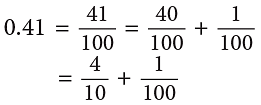
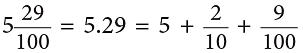
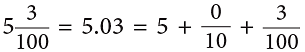
 In the above number, there are 2 decimal places after the whole number part.
In the above number, there are 2 decimal places after the whole number part. the correct one?
the correct one?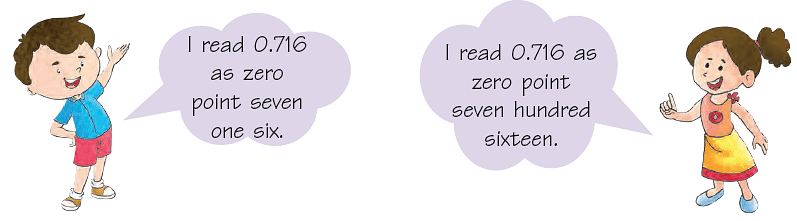
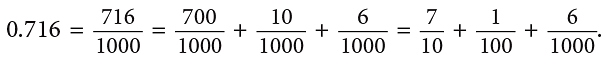
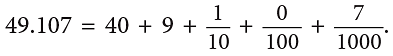
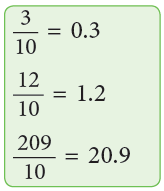
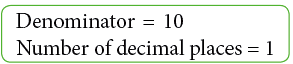
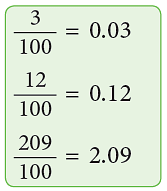
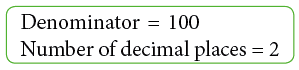
 Pictorial representation of how to convert a decimal to a fraction
Pictorial representation of how to convert a decimal to a fraction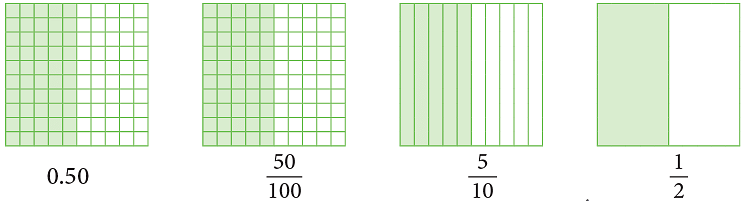
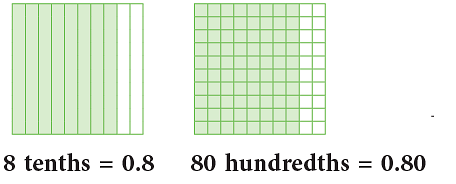 As can be seen, these two pictures name the same amount, so 0.8 = 0.80.
As can be seen, these two pictures name the same amount, so 0.8 = 0.80.