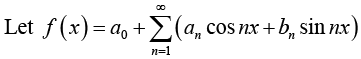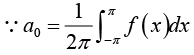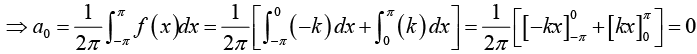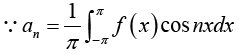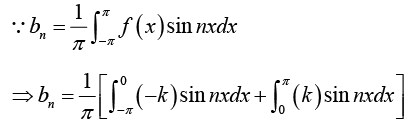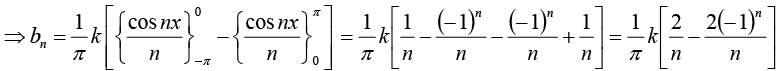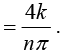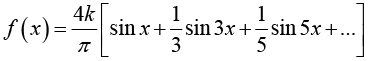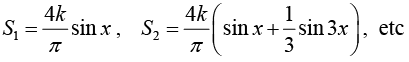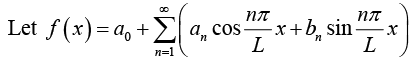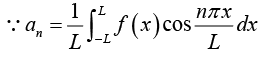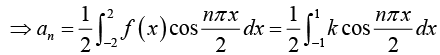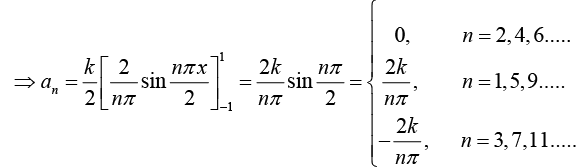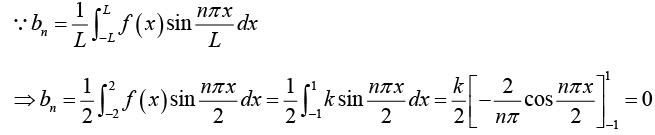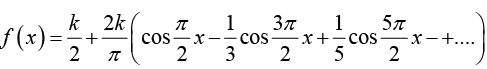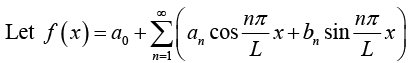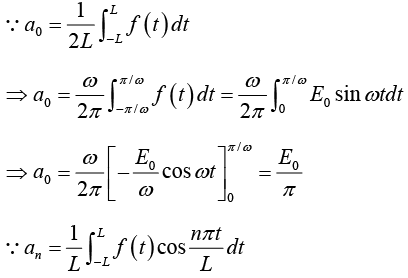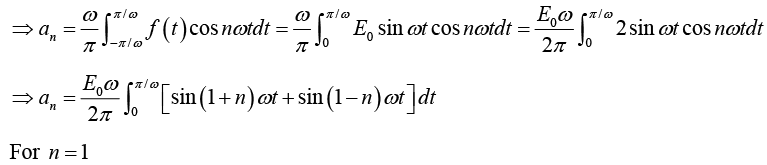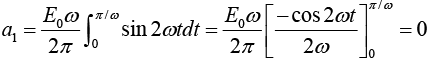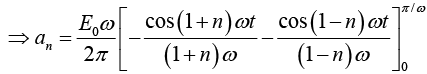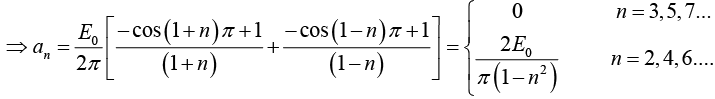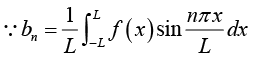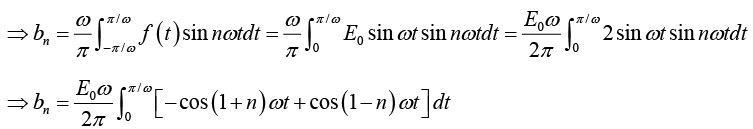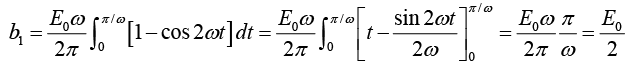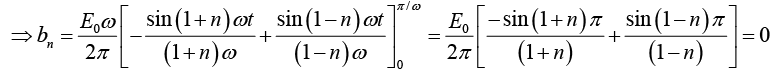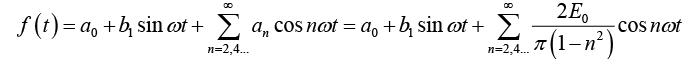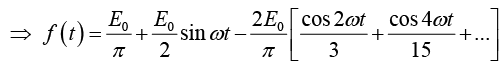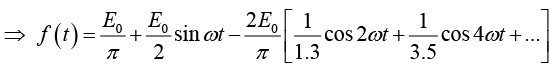Periodic Functions & Trigonometric Series | Mathematical Methods - Physics PDF Download
Periodic Functions
A function f (x) is called periodic if for all real x in the domain of f (x) there is some positive number p such that
f (x + p ) = f (x) for all x .
The number p is called period of f (x) . The graph of such function is obtained by periodic repetition of its graph in any interval of length p .
NOTE:
(i) Familiar periodic functions are sine and cosine functions.
(ii) The function f = constant is also a periodic function.
(iii) The functions that are not periodic are x, x2, x3, ex, cosh x, ln x etc.
(iv) ∵ f (x+2 p) = f [(x + p)+p ] = f (x + p)=f (x) Thus for any integer n , f (x + np) = f (x). Hence 2p ,3p,...... are also period of f (x) .
(v) If f (x) and g (x) have period p , then the function h (x) = af (x) + bg (x) (a, b constants) has also period p .
Fundamental Period
If a periodic function f (x) has a smallest period p (> 0) , this is often called the fundamental period of f (x).
Example:
(i) For sin x and cos x the fundamental period is 2π .
(ii) For sin 2x and cos 2x the fundamental period is π.
(iii) For tan x and cot x the fundamental period is π.
(iv) A functions without fundamental period is f = constant.
Trigonometric Series
Let’s represent various functions of period p = 2π in terms of simple functions1, cos x, sin x, cos 2x, sin2x, cos nx, sin nx,
These functions have period 2π. Figure below shows the first few of them.
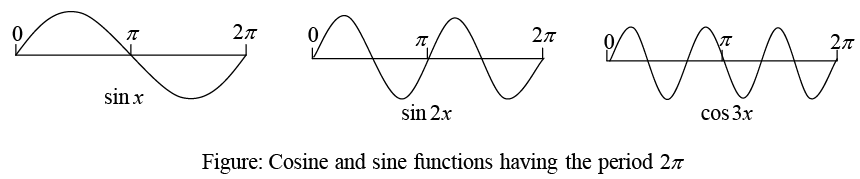
The series that will arise in this connection will be of the form
a0 + a1 cos x + b1 sin x + a2cos 2 x + b2 sin 2 x + ..........
Where a0,a1,a2...b1,b2... are real constants. Such a series is called trigonometric seris and the an and bn are called the coefficient of the series. Thus we may write series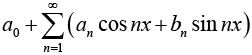
We see that each term of the series has the period 2π . Hence if the series converges, its sum will be a function of period 2π .
NOTE:
The trignometric series can be used for representing any practically important periodic function f, simple or complicated, of any period p . This series will then be called the Fourier series of f.
Fourier Series
Fourier series arise from the practical task of representing a given periodic function f (x) in terms of cosine and sine functions. These series are trigonometric series whose coefficients are determined from f (x) by the “Euler Formulas”.
Formulas for the Fourier Coefficients
Let us assume that f(x) is periodic function of period 2π and is integrable over a period. Let us further assume that f(x) can be represented by a trigonometric series, (assume that this series converges and has f(x) as its sum)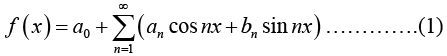
Determination of constant a0:
From equation (1), we have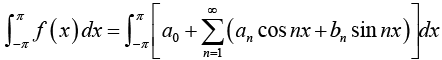
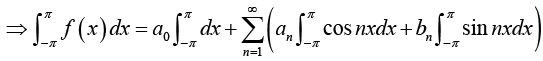
Thus 
Determination of constant an :
Multiply equation (1) by cos mx. where m is any fixed positive integer, then
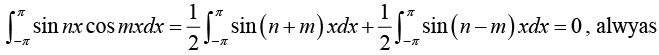
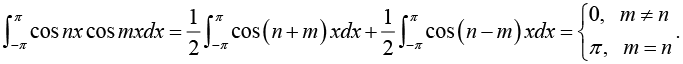
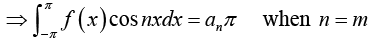
Thus 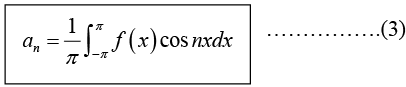
Determination of constant bn:
Multiply equation (1) by sin mx, where m is any fixed positive integer, then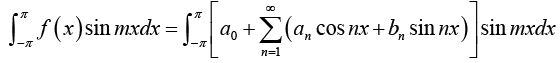
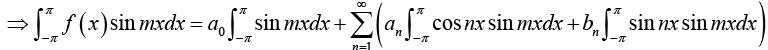
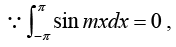
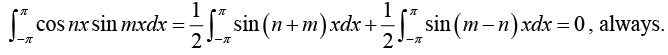
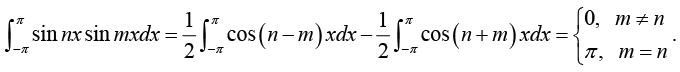
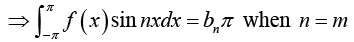
Thus 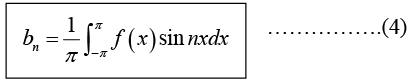
Example 1: Find the Fourier coefficient of the periodic function f(x) as shown in figure:
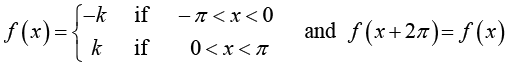
Hence, show that: 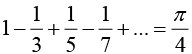
This can also be seen without integration, since the area under the curve of f(x) between -π to π is zero.
If n is even bn = 0 and If n is odd bn
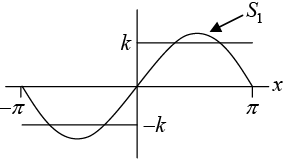
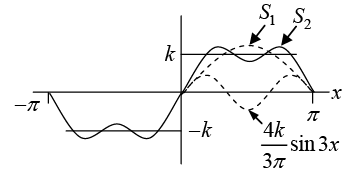
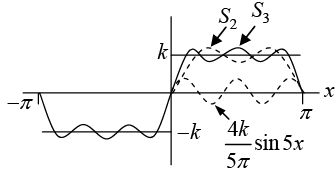
Thus Fourier series is
The partial sums are
Figure(a): The given function f (x) (Period square wave)
Figure(b): The first three partial sums of the corresponding Fourier series
NOTE:
The above graph seems to indicate that the series is convergent and has the sum f(x),
the given function. Notice that at x = 0 and x = π , the points of discontinuity of f (x), all
partial sums have the value zero, the arithmetic mean of the values -k and +k of our function.
Assuming that f (x) is the sum of the series and setting x = 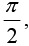 we have
we have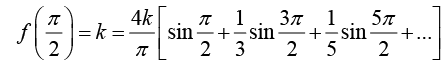
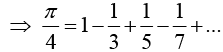
Orthogonality of the Trignometric System
The trigonometric system
1, cos x, sin x, cos 2x, sin 2x,......cos nx, sin nx,
is orthogonal on the interval -n < x < n (hence on any interval of length 2π , because of periodicity). Thus for any integer m and n we have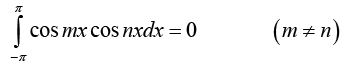
and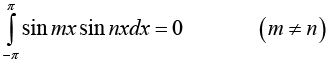
and for any integer m and n (including m = n) we have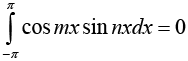
Convergence and Sum of Fourier Series
If a periodic function f(x) with period 2π is piecewise continuous in the interval -n<x<n and has left hand and right hand derivative at each point of that interval, then the Fourier series of f(x) with coefficient a0,an,bn is convergent.
Its sum is f (x), except at a point x0 at which f (x) is discontinuous and the sum of the series is the average of the left- and right-hand limit of / (x) at x0.
NOTE:
(i) The left-hand limit of f (x) at x0 is 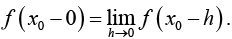
The right-hand limit of f (x) at x0 is 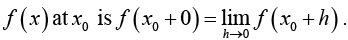
(ii) The left-hand derivative of f(x) at x0 is 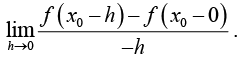
The right-hand derivative of f (x) at x0 is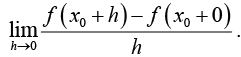
(iii) If f (x) is continuous at x0, then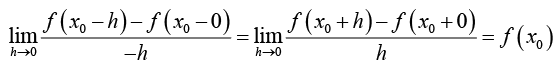
Example: The square wave in previous example has a jump atx = 0 . Its left-hand limit there is -k and its left-hand limit there is +k . Hence average of these limits is 0 . Tlius Fourier series converge to this value atx = 0 because then all its tenns areO. Similarly for the other jump w e can verify this.
Function of Any Period p = 2L
The functions considered so far had period 2π , for simplicity. The transition from p = 2π to p = 2L is quite simple. It amounts to a stretch (or contraction) of scale on the axis.
Fourier series of a function f (x) of period p = 2L. is given by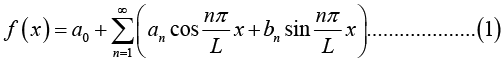
where Fourier coefficients of f (x) are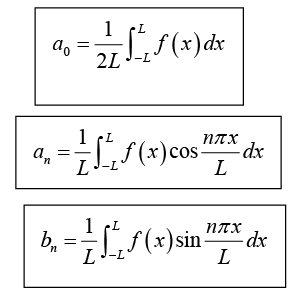
Let 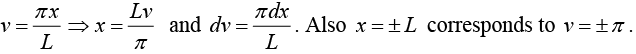
Thus, f (x) = g (v) has period 2π .
Hence we can verify that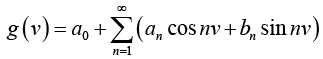
where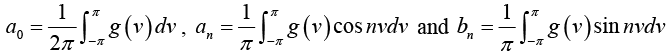
Example 2: Find the Fourier series of the function/(x) as shown in figure:
Thus Fourier series is
Example 3: A sinusoidal voltage E0 sin ωt, where t is time, is passed through half-wave
rectifier that clips the negative portion of the wave. Find the Fourier series of the resulting periodic function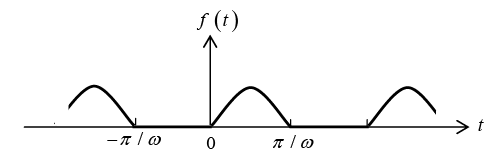
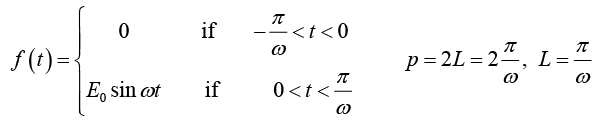
For n = 2,3,4....
For n = 1
For n = 2,3,4...
Thus Fourier series
|
78 videos|18 docs|24 tests
|
FAQs on Periodic Functions & Trigonometric Series - Mathematical Methods - Physics
| 1. What is a Fourier series? |  |
| 2. What is the period of a Fourier series? |  |
| 3. What are periodic functions? |  |
| 4. How are Fourier series used in IIT JAM? |  |
| 5. Are trigonometric series and Fourier series the same thing? |  |