NCERT Exemplar Solutions: Triangles | Mathematics (Maths) Class 7 PDF Download
In each of the questions 1 to 49, four options are given, out of which only one is correct. Choose the correct one.
Q.1. The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is
(a) 6
(b) 5
(c) 3
(d) 4
Ans: (d)
Explanation: In the question two sides are given, 10 and 6.5.
We know that, the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
So, 6.5 + a = 10
a > 10 – 6.5
a > 3.5 i.e. 4
Q.2. Triangle DEF of Fig. 6.6 is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F? (a) They are equal angles
(a) They are equal angles
(b) They form a pair of adjacent angles
(c) They are complementary angles
(d) They are supplementary angles
Ans: (c)
Q.3. In Fig. 6.7, PQ = PS. The value of x is (a) 35o
(a) 35o
(b) 45o
(c) 55o
(d) 70o
Ans: (b)
Explanation: From the given figure,
In triangle PQS, ∠PSQ + ∠QPS = 110o … [from exterior angle property of a triangle]
We know that, sum of all angles of the triangle is equal to 180o.
So, ∠PSQ + ∠QPS + ∠PQS = 180o
∠PQS = 180o – 110o
∠PQS = 70o
Now, consider the triangle PRS,
∠PSQ = x + 25o … [from the exterior angle property of a triangle]
x = 70o – 25o
x = 45o
Q.4. In a right-angled triangle, the angles other than the right angle are
(a) Zobtuse
(b) Right
(c) Acute
(d) Straight
Ans: (c)
Q.5. In an isosceles triangle, one angle is 70°. The other two angles are of
(i) 55° and 55°
(ii) 70° and 40°
(iii) any measure
In the given options which of the above statements are true?
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (i) and(ii)
Ans: (d)
Explanation: From the question it is given that,
One angle of an isosceles triangle is 70o.
We know that, in an isosceles triangle 2 angles are equal corresponding with 2 equal sides,
If 70o is 3rd angle of triangle,
70o + x + x = 180o
2x + 70o = 180o
2x = 180o – 70o
x = (110o/2)
x = 55o
So, both angles are 55o
Consider the 70o as base angle of an isosceles triangle
Then, 70o + 70o + x = 180o
x = 180o – 140o
x = 40o
So, one angle is 40o and another is 70o
Q.6. In a triangle, one angle is of 90°. Then
(i) The other two angles are of 45° each
(ii) In remaining two angles, one angle is 90° and other is 45°
(iii) Remaining two angles are complementary In the given option(s) which is true
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (i) and (ii)
Ans: (c)
Q.7. Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is
(a) Obtuse angled triangle
(b) Acute-angled triangle
(c) Right-angled triangle
(d) An Isosceles right triangle
Ans: (c)
Q.8. In Fig. 6.8, PB = PD. The value of x is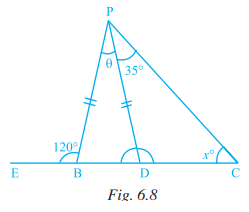 (a) 85o
(a) 85o
(b) 90o
(c) 25o
(d) 35o
Ans: (c)
Explanation: Exterior angle of triangle is equal to sum of 2 opposite interior angles.
As BC is straight line
∠PBD + 120° = 180°
∠PBD = 180° – 120°
∠PBD = 60°
Given in an isosceles ΔPBD, PB = PD
∴ ∠PBD = ∠PDB
With exterior angle ∠PSQ equal to sum of opposite interior angles
∠PDB = ∠DPC + ∠PCD [Exterior Angle Property]
60° = x + 35°
x = 60° – 35°
x = 25°
Q.9. In ∆PQR,
(a) PQ – QR > PR
(b) PQ + QR < PR
(c) PQ – QR< PR
(d) PQ + PR< QR
Ans: (c)
Explanation: The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.
Q.10. In ∆ ABC,
(a) AB + BC > AC
(b) AB + BC < AC
(c) AB + AC < BC
(d) AC + BC < AB
Ans: (a)
Explanation: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
Q.11. The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is
(a) 25 m
(b) 13 m
(c) 18 m
(d) 17 m
Ans: (c)
Explanation: From the question it is given that,
The top of a broken tree touches the ground at a distance of 12 m from its base
The broken height of the tree = 5 m
By using Pythagoras theorem,
Hypotenuse2 = Base2 + Height2
Hypotenuse2 = 122 + 52
Hypotenuse2 = 144 + 25
Hypotenuse2 = 169
Hypotenuse = √169
Hypotenuse = 13
So, the total height of tree = 5 + 13 = 18 m
Q.12. The triangle ABC formed by AB = 5 cm, BC = 8 cm, AC = 4 cm is
(a) an isosceles triangle only
(b) a scalene triangle only
(c) an isosceles right triangle
(d) scalene as well as a right triangle
Ans: (b)
Explanation: A scalene triangle is a triangle that has three unequal sides.
Q.13. Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is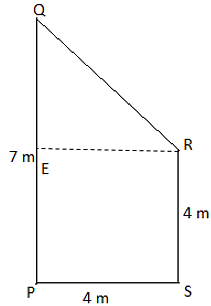 (a) 3 m
(a) 3 m
(b) 5 m
(c) 4 m
(d) 11 m
Ans: (b)
Explanation: Consider PQ is the tree of height 7m and RS is the tree of height 4 m.
So, consider the triangle QRE, from the Pythagoras theorem,
QR2 = QE2 + ER2
QR2 = 32 + 42
QR2 = 9 + 16
QR2 = 25
QR = √25
QR = 5
Therefore, the distance between the top of the two trees is 5m.
Q.14. If in an isosceles triangle, each of the base angles is 40°, then the triangle is
(a) Right-angled triangle
(b) Acute angled triangle
(c) Obtuse angled triangle
(d) Isosceles right-angled triangle
Ans: (c)
Explanation: We know that, sum of interior angles of triangle is equal to 180o.
Let us assume the 3rd angle be Q,
Then, 40o + 40o + Q = 180o
80o + Q = 180o
Q = 180 – 80
Q = 100o
An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles. Since a triangle’s angles must sum to 180o.
Q.15. If two angles of a triangle are 60° each, then the triangle is
(a) Isosceles but not equilateral
(b) Scalene
(c) Equilateral
(d) Right-angled
Ans: (c)
Explanation: In an equilateral triangle, each angle has measure 60o.
Q.16. The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is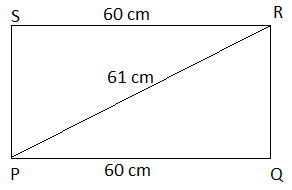 (a) 120 cm
(a) 120 cm
(b) 122 cm
(c) 71 cm
(d) 142 cm
Ans: (d)
Explanation: Consider the rectangle PQRS,
Given, length of rectangle PQ = 60 cm, Diagonal of the rectangle = 61 cm.
To find out the height of the rectangle, consider the right angled triangle PQR.
From the Pythagoras theorem, PR2 = PQ2 + RQ2
612 = 602 + RQ2
3721 = 3600 + RQ2
RQ2 = 3721 – 3600
RQ2 = 121
RQ = √121
RQ = 11 cm
Then, the perimeter of the rectangle PQRS = 2 (Length + Breadth)
= 2 (60 + 11)
= 2 (71)
= 142 cm
Q.17. In ∆PQR, if PQ = QR and ∠Q = 100o, then ∠R is equal to
(a) 40o
(b) 80o
(c) 120o
(d) 50o
Ans: (a)
Explanation: Given, In ∆PQR, PQ = QR so it is an isosceles triangle.
Then, ∠P = ∠R
So, let us assume two angles be x
x + x + 100o = 180o
2x = 180o – 100o
2x = 80o
x = 80o/2
x = 40o
Therefore, x = ∠P = ∠R = 40o
Q.18. Which of the following statements is not correct?
(a) The sum of any two sides of a triangle is greater than the third side
(b) A triangle can have all its angles acute
(c) A right-angled triangle cannot be equilateral
(d) Difference of any two sides of a triangle is greater than the third side
Ans: (d)
Explanation: The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.
Q.19. In given figure, BC = CA and ∠A = 40. Then, ∠ACD is equal to (a) 40o
(a) 40o
(b) 80o
(c) 120o
(d) 60o
Ans: (b)
Explanation: We know that, the exterior angle is equal to sum of opposite interior angles.
So, ∠ACD = ∠A + ∠B
As ΔACB is an isosceles triangle with AC = BC
Therefore, ∠A must be equal to ∠B
∠ACD = 40o + 40o
= 80o
Q.20. The length of two sides of a triangle are 7 cm and 9 cm. The length of the third side may lie between
(a) 1 cm and 10 cm
(b) 2 cm and 8 cm
(c) 3 cm and 16 cm
(d) 1 cm and 16 cm
Ans: (c)
Explanation: From the question it is given that, the length of two sides of a triangle are 7 cm and 9 cm.
Let us assume the length of the third side of the triangle be ‘P’.
We Know that, the sum of the two sides of the triangle is greater than the third side.
So, 7 + 9 > P
16 > P
Now, difference between two sides = 9 – 7 = 2
Therefore, the third side is greater than 2 and smaller than 16.
i.e. 3 cm and 16 cm
Q.21. From given Fig. , the value of x is 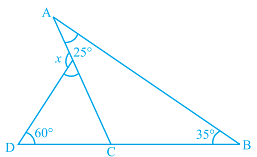 (a) 75o
(a) 75o
(b) 90o
(c) 120o
(d) 60o
Ans: (c)
Explanation: We know that, exterior angle is equal to sum of opposite interior angles.
From the figure,
∠ACD = ∠A + ∠B
∠ACD = 25o + 35o
= 60°
Then, in another triangle
x is exterior angle
∴ x = 60° + ∠ACD
x = 60° + 60°
x = 120°
Q.22. In given Fig. , the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is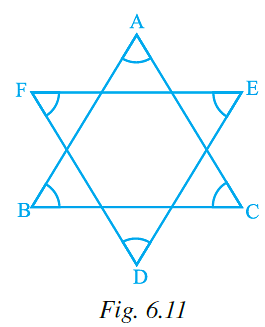 (a) 190o
(a) 190o
(b) 540o
(c) 360o
(d) 180o
Ans: (c)
Explanation: From the figure, we can able to find out there are two triangles.
So, consider the ΔABC,
We know that, sum of the interior angles of the triangle is equal to 180o.
Therefore, ∠A + ∠B + ∠C = 180o
Now, consider the ΔDEF,
∠D + ∠E + ∠F = 180o
Then,
= ∠A + ∠B + ∠C + ∠D + ∠E + ∠F
= 180o + 180o
= 360o
Q.23. In given Fig. , PQ = PR, RS = RQ and ST || QR. If the exterior angle RPU is 140°, then the measure of angle TSR is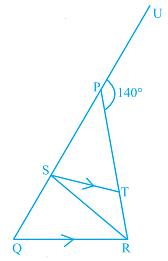 (a) 55°
(a) 55°
(b) 40°
(c) 50°
(d) 45°
Ans: (b)
Explanation: Consider the ΔPQR.
From the exterior angle property
∠RPU = ∠PRQ + ∠PQR
140O = 2 ∠PQR … [given PQ = PR]
∠PQR = 140/2
∠PQR = 70o
Given, ST || QR and QS is transversal.
From the property of corresponding angles, ∠PST = ∠PQR = 70o
Now, consider the ΔQSR
RS = RQ … [from the question]
So, ∠SQR = ∠RSQ = 70O
Then, PQ is a straight line.
∠PST + ∠TSR + ∠RSQ = 180o
70o + ∠TSR + 70o = 180o
140o + ∠TSR = 180o
∠TSR = 180o – 140o
∠TSR = 40o
Q.24. In Fig. 6.13, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is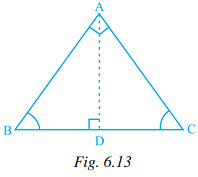 (a) 50°
(a) 50°
(b) 40°
(c) 70°
(d) 60°
Ans: (a)
Explanation: From the question it is given that, ∠BAC = 90o AD ⊥ BC and ∠BAD = 50o
So, ∠DAC = ∠BAC – ∠BAD
= 90o – 50o
= 40o
The, consider the ΔADC
From the rule of exterior angle property = ∠ADB = ∠DAC + ∠ACD
90o = 40o + ∠ACD
∠ACD = 90 – 40
∠ACD = 50o
Q.25. If one angle of a triangle is equal to the sum of the other two angles, the triangle is
(a) Obtuse
(b) Acute
(c) Right
(d) Equilateral
Ans: (c)
Q.26. If the exterior angle of a triangle is 130° and its interior opposite angles are equal, then measure of each interior opposite angle is
(a) 55o
(b) 65o
(c) 50o
(d) 60o
Ans: (b)
Explanation: Let us assume the interior opposite angles are Q and Q.
Then, 130o = Q + Q … [from exterior angle property]
2Q = 130o
Q = 130o/2
Q = 65o
Therefore, the measure of each interior opposite angle is 65o.
Q.27. If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is
(a) 70o
(b) 110o
(c) 35o
(d) 145o
Ans: (d)
Explanation: From the question it is given that, one of the angles of triangle is 110o
We know that, sum of all angles of triangle is equal to 180o.
So, sum of other 2 angles is 180o – 110o = 70o
Then, both angles get halved 70o/2 = 35o
Sum of bisected angles will be half of sum of angles of triangle.
Then, the third angle will be = 180o – 35o
= 145o
Q.28. In ∆ABC, AD is the bisector of ∠A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is (a) AD
(a) AD
(b) BE
(c) FC
(d) DE
Ans: (b)
Explanation: We know that the median of triangle divides the opposite side into two equal parts.
Hence, BE is the median (as AE = EC).
Q.29. In ∆PQR, if ∠ P = 60o, and ∠ Q = 40o, then the exterior angle formed by producing QR is equal to
(a) 60o
(b) 120o
(c) 100o
(d) 80o
Ans: (c)
Explanation: As we know that, exterior angle is sum of opposite interior angles.
Then, the exterior angle formed by producing QR
It has opposite interior angles ∠P and ∠Q
Therefore, exterior angle = ∠P + ∠Q
= 60o + 40o
= 100o
Q.30. Which of the following triplets cannot be the angles of a triangle?
(a) 67°, 51°, 62°
(b) 70°, 83°, 27°
(c) 90°, 70°, 20°
(d) 40°, 132°, 18°
Ans: (d)
Explanation: We know that, sum of angles of triangle is equal to 180o.
But, 40o + 132o + 18o = 190
So, these triplets cannot be the angles of a triangle.
Q.31. Which of the following can be the length of the third side of a triangle whose two sides measure 18 cm and 14 cm?
(a) 4 cm
(b) 3 cm
(c) 5 cm
(d) 32 cm
Ans: (c)
Explanation: We know that, the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
So, 18 cm + 14 cm > 3rd side
3rd side < 32 cm
The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.
So, 18 – 14 < 3rdside
3rd side > 4 cm
Therefore, 5 cm is the length of the 3rd side.
Q.32. How many altitudes does a triangle have?
(a) 1
(b) 3
(c) 6
(d) 9
Ans: (b)
Explanation: The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle. A triangle has 3 altitudes.
Q.33. If we join a vertex to a point on opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?
(a) Median
(b) Angle bisector
(c) Altitude
(d) Hypotenuse
Ans: (a)
Explanation: The line segment joining a vertex of a triangle to the mid point of its opposite side is called a median of the triangle.
Q.34. The measures of ∠x and ∠y in Fig. 6.14 are respectively (a) 30°, 60°
(a) 30°, 60°
(b) 40°, 40°
(c) 70°, 70°
(d) 70°, 60°
Ans: (d)
Explanation: We know that, the exterior angle is sum of interior opposite angles of triangle.
So, x + 50o = 120o
x = 120o – 50o
x = 70o
We also know that, sum of angles of triangle are equal to 180o.
So, 50o + x + y = 180o
50o + 70o + y = 180o
120o + y = 180o
y = 180o – 120o
y = 60o
Therefore, the measures of ∠x and ∠y is 70o and 60o respectively.
Q.35. If length of two sides of a triangle are 6 cm and 10 cm, then the length of the third side can be
(a) 3 cm
(b) 4 cm
(c) 2 cm
(d) 6 cm
Ans: (d)
Explanation: We know that,
The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
So, 6 cm + 10 cm > 3rd side
3rd side < 16 cm
The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.
So, 10 – 6 < 3rd side
3rd side > 4 cm
Therefore, 6 cm is the length of the 3rd side.
Q.36. In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 6 cm
Ans: (b)
Explanation: From Pythagoras theorem.
AC2 = AB2 + BC2
52 = AB2 + 32
AB2 = 25 – 9
AB2 = 16
AB = √16
AB = 4 cm
Q.37. In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
(a) AB2 = BC2 + AC2
(b) AC2 = AB2 + BC2
(c) AB = BC + AC
(d) AC = AB + BC
Ans: (b)
Explanation: AC2 = AB2 + BC2 … [from Pythagoras theorem] 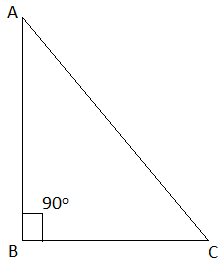
Q.38. Which of the following figures will have its altitude outside the triangle?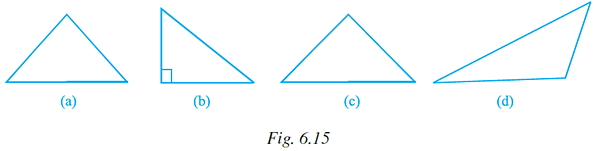
Ans: (d)
Q.39. In Fig. 6.16, if AB || CD, then,
(a) ∠ 2 = ∠ 3
(b) ∠ 1 = ∠ 4
(c) ∠ 4 = ∠ 1 + ∠ 2
(d) ∠ 1 + ∠ 2 = ∠ 3 + ∠ 4
Ans: (d)
Explanation: As we know that, exterior angle is equal to the sum of opposite interior angles
Consider, Δ ABC
As BC is extended
∠A + ∠B = ∠3 + ∠4
Therefore, ∠1 + ∠2 = ∠3 + ∠4
Q.40. In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD⊥BC. Then, ∠B is equal to
(a) 80o
(b) 20o
(c) 40o
(d) 30o
Ans: (c)
Explanation: Consider the triangle ABC,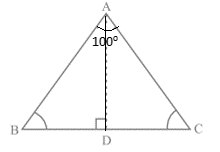
From the figure, AD bisects ∠Α
Then, ∠BAD = 50o
∠DAC = 50o
So, AD⊥BC
∠ΑDC = 90o
Consider the ∆ABD,
From the rule of exterior angle property of triangle,
∠ΑDC = ∠ΑBD + ∠BAD
90o = ∠ΑBD + 50o
∠ΑBD = 90o – 50o
= 40o
Q.41. In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (Fig. 6.17). Measure of ∠ADC is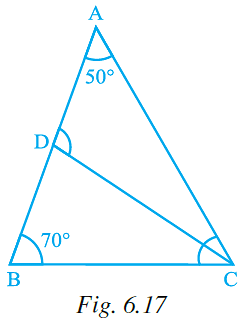
(a) 50°
(b) 100°
(c) 30°
(d) 70°
Ans: (b)
Explanation: From the figure,
Consider the ΔABC,
We know that, sum of angles of triangle is equal to 180o.
So, ∠Α + ∠B + ∠C = 180o
50o + 70o + ∠C = 180o
∠C + 120o = 180o
∠C = 180o – 120o
∠C = 60o
Since CD bisects ∠C,
So, ∠DCB = ∠ΑCD = ½ ∠C
= 60o/2
= 30o
Now, consider ΔBDC
From exterior angle property, ∠ADC = ∠DBC + ∠DCB
∠ADC = 70o + 30o
= 100o
Q.42. If for ∆ABC and ∆DEF, the correspondence CAB ↔ EDF gives a congruence, then which of the following is not true?
(a) AC = DE
(b) AB = EF
(c) ∠A = ∠D
(d) ∠C = ∠E
Ans: (b)
Explanation: Because, for ∆ABC and ∆DEF
AB = DF
Q.43. In Fig. 6.18, M is the mid-point of both AC and BD. Then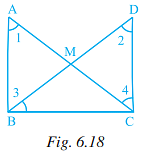 (a) ∠1 = ∠2
(a) ∠1 = ∠2
(b) ∠1 = ∠4
(c) ∠2 = ∠4
(d) ∠1 = ∠3
Ans: (b)
Explanation: From the figure, M is the mid-point of both AC and BD.
By the corresponding parts of congruent triangles, ∠1 = ∠4.
Q.44. If D is the mid-point of the side BC in ∆ABC where AB = AC, then ∠ADC is
(a) 60°
(b) 45°
(c) 120°
(d) 90°
Ans: (d)
Explanation: We know that, in an isosceles triangle altitude and median are the same.
From the question, if D is the mid-point of the side BC in ∆ABC
Where, D is midpoint of BC joining from point A gives AD as median.
It possess 90o angle on BC
Therefore, ∠ADC = 90o
Q.45. Two triangles are congruent, if two angles and the side included between them in one of the triangles are equal to the two angles and the side included between them of the other triangle. This is known as the
(a) RHS congruence criterion
(b) ASA congruence criterion
(c) SAS congruence criterion
(d) AAA congruence criterion
Ans: (b)
Q.46. By which congruency criterion, the two triangles in Fig. 6.19 are congruent?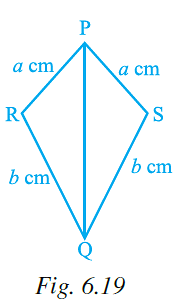 (a) RHS
(a) RHS
(b) ASA
(c) SSS
(d) SAS
Ans: (c)
Explanation: Under a given correspondence, two triangles are congruent, if the three sides of the one are equal to the three sides of the other.
Q.47. By which of the following criterion two triangles cannot be proved congruent?
(a) AAA
(b) SSS
(c) SAS
(d) ASA
Ans: (a)
Explanation: In AAA criterion two triangles cannot be proved congruent.
Q.48. If ∆PQR is congruent to ∆STU (Fig. 6.20), then what is the length of TU?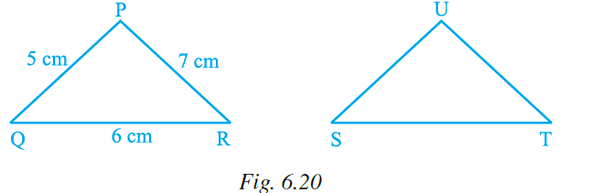 (a) 5 cm
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) cannot be determined
Ans: (b)
Explanation: From the question it is given that,
Δ PQR ≅ Δ STU
So,
PQR ↔ STU
∴ QR = TU
TU = 6cm
Q.49. If ∆ABC and ∆DBC are on the same base BC, AB = DC and AC = DB (Fig. 6.21), then which of the following gives a congruence relationship?
(a) ∆ ABC ≅ ∆ DBC
(b) ∆ ABC ≅ ∆CBD
(c) ∆ ABC ≅ ∆ DCB
(d) ∆ ABC ≅ ∆BCD
Ans: (c)
Explanation: Consider the ΔABC and ΔDCB,
From the question it is given that, AB = DC and AC = DB
BC = BC … [because common side]
Therefore, ∆ ABC ≅ ∆ DCB
In questions 50 to 69, fill in the blanks to make the statements true.
Q.50. The triangle always has altitude outside itself.
Solution: The Obtuse triangle always has altitude outside itself.
Q.51. The sum of an exterior angle of a triangle and its adjacent angle is always.
Solution: The sum of an exterior angle of a triangle and its adjacent angle is always 1800.
Q.52. The longest side of a right angled triangle is called its .
Solution: The longest side of a right angled triangle is called its hypotenuse.
Q.53. Median is also called in an equilateral triangle.
Solution: Median is also called altitude in an equilateral triangle
Q.54. Measures of each of the angles of an equilateral triangle is .
Solution: Measures of each of the angles of an equilateral triangle is 60o.
Q.55. In an isosceles triangle, two angles are always .
Solution: In an isosceles triangle, two angles are always equal.
Q.56. In an isosceles triangle, angles opposite to equal sides are.
Solution: In an isosceles triangle, angles opposite to equal sides are equal.
Q.57. If one angle of a triangle is equal to the sum of other two, then the measure of that angle is.
Solution: If one angle of a triangle is equal to the sum of other two, then the measure of that angle is 90o.
Q.58. Every triangle has at least acute angles.
Solution: Every triangle has at least two acute angles.
Q.59. Two line segments are congruent, if they are of lengths.
Solution: Two line segments are congruent, if they are of equal lengths.
Q.60. Two angles are said to be , if they have equal measures.
Solution: Two angles are said to be congruent, if they have equal measures.
Q.61. Two rectangles are congruent, if they have same .
Solution: Two rectangles are congruent, if they have same length and breadth.
Q.62. Two squares are congruent, if they have same.
Solution: Two squares are congruent, if they have same side.
Q.63. If ∆PQR and ∆XYZ are congruent under the correspondence QPR ↔ XYZ, then
(i) ∠R =
(ii) QR =
(iii) ∠P =
(iv) QP =
(v) ∠ Q =
(vi) RP =
Solution: If ∆PQR and ∆XYZ are congruent under the correspondence QPR ↔ XYZ, then
(i) ∠R = ∠Z
(ii) QR = XZ
(iii) ∠P = ∠Y
(iv) QP = XY
(v) ∠Q = ∠X
(vi) RP = ZY
Q.64. In Fig. 6.22, ∆PQR ≅ ∆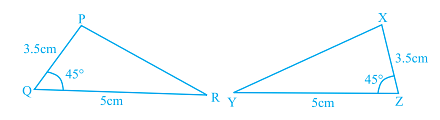 Fig. 6.22
Fig. 6.22
Solution: In Fig. 6.22, ∆PQR ≅ ∆XZY
From the figure, PQ = XZ = 3.5 cm
QR = ZY = 5cm
∠PQR = ∠XZY = 45o
From SAS criterion, ∆PQR ≅ ∆XZY
Q.65. In Fig. 6.23, ∆PQR ≅ ∆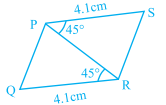
Solution: In Fig. 6.23, ∆PQR ≅ ∆RSP
From the figure, PS = RQ = 4.1 cm
PR = PR … [common side for both triangles]
∠PRQ = ∠RPS = 45o
From SAS criterion, ∆PQR ≅ ∆RSP
Q.66. In Fig. 6.24, ∆ ≅ ∆ PQR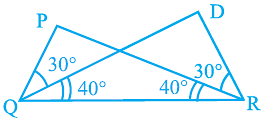
Solution: In Fig. 6.24, ∆DRQ ≅ ∆ PQR
From the figure,
QR = QR … [common side for both triangles]
∠PRQ = ∠DQR = 40o
∠PQR = ∠DRQ = 70o
From ASA criterion, ∆DRQ ≅ ∆ PQR
Q.67. In Fig. 6.25, ∆ ARO ≅ ∆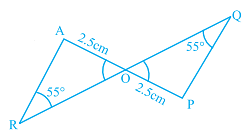
Solution: In Fig. 6.25, ∆ ARO ≅ ∆PQO
From the figure,
AO = PO = 2.5 cm
∠ARO = ∠PQO = 55o
∠AOR = ∠POQ [vertically opposite angles]
From ASA criterion, ∆ARO ≅ ∆ PQO
Q.68. In Fig. 6.26, AB = AD and ∠BAC = ∠ DAC. Then
(i) ∆ ≅ ∆ ABC.
(ii) BC = .
(iii) ∠BCA = .
(iv) Line segment AC bisects and.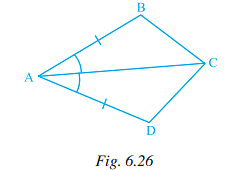
Solution: In Fig. 6.26, AB = AD and ∠BAC = ∠ DAC.
Then (i) ∆ADC ≅ ∆ ABC.
(ii) BC = DC.
(iii) ∠BCA = ∠DCA.
(iv) Line segment AC bisects ∠BAD and ∠BCD.
Q.69. In Fig. 6.27,
(i) ∠ TPQ = ∠ _____ + ∠ _____
(ii) ∠ UQR = ∠ _____ + ∠ _____
(iii) ∠ PRS = ∠ _____ + ∠ _____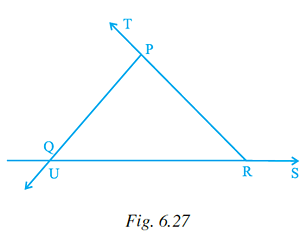
Solution: In Fig. 6.27,
(i) ∠ TPQ = ∠ PQR + ∠ PRQ … [from exterior angle property]
(ii) ∠ UQR = ∠ QRP + ∠ QPR … [from exterior angle property]
(iii) ∠ PRS = ∠ RPQ + ∠ RQP … [from exterior angle property]
In questions 70 to 80 state whether the statements are True or False.
Q.70. In a triangle, sum of squares of two sides is equal to the square of the third side.
Solution: False
In a right angled triangle, sum of squares of two sides is equal to the square of the third side.
Q.71. Sum of two sides of a triangle is greater than or equal to the third side.
Solution: False
The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
Q.72. The difference between the lengths of any two sides of a triangle is smaller than the length of third side.
Solution: True.
Q.73. In ∆ABC, AB = 3.5 cm, AC = 5 cm, BC = 6 cm and in ∆PQR, PR= 3.5 cm, PQ = 5 cm, RQ = 6 cm. Then ∆ABC ≅ ∆PQR.
Solution: False
In ∆ABC, AB = 3.5 cm, AC = 5 cm, BC = 6 cm and in ∆PQR, PR= 3.5 cm, PQ = 5 cm, RQ = 6 cm. Then ∆ABC ≅ ∆PRQ
Q.74. Sum of any two angles of a triangle is always greater than the third angle.
Solution: False
Sum of any two angles of a triangle is either greater than the third angle or smaller than the third angle.
Q.75. The sum of the measures of three angles of a triangle is greater than 180o.
Solution: False
The sum of the measures of three angles of a triangle is equal to 180o.
Q.76. It is possible to have a right-angled equilateral triangle.
Solution: False
In a right angled triangle, sum of squares of two sides is equal to the square of the third side.
But, in equilateral triangle all sides are always equal.
Q.77. If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent.
Solution: True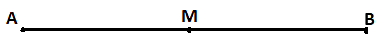
In the figure, M is the midpoint,
So, AM = MB
Q.78. It is possible to have a triangle in which two of the angles are right angles.
Solution: False.
It is not possible to have a triangle in which two of the angles are right angles.
Q.79. It is possible to have a triangle in which two of the angles are obtuse.
Solution: False.
It is not possible to have a triangle in which two of the angles are obtuse.
Q.80. It is possible to have a triangle in which two angles are acute.
Solution: True.
Q.81. It is possible to have a triangle in which each angle is less than 60°
Solution: False
If all angles of a triangle are less than 60°, then their sum will be less than 180°. But in a triangle sum of all angles is 180°.
∴ Triangle is not possible.
Q.82. It is possible to have a triangle in which each angle is greater than 60°
Solution: False
If all angles of a triangle are greater than 60°, then their sum will be greater than 180°. But in a triangle sum of all angles is 180°
∴ Triangle is not possible.
Q.83. It is possible to have a triangle in which each angle is equal to 60°
Solution: True
Since in equilateral triangle each angle is equal to 60°.
Q.84. A right-angled triangle may have all sides equal.
Solution: False
A right-angled triangle may have two sides equal.
Q.85. If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
Solution:
False
If two angles of a triangle are equal then third angle may or may not be equal to each of the other two angles.
Q.86. In the given figure, two triangles are congruent by RHS.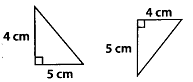 Solution: FalseSince, given triangles are congruent by SAS.
Solution: FalseSince, given triangles are congruent by SAS.
Q.87. The congruent figures superimpose each other completely.
Solution: True
Q.88. A one rupee coin is congruent to a five rupee coin.
Solution:
False
Since, one rupee coin and five rupee coin are of different size so they are not congruent.
Q.89. The top and bottom faces of a kaleidoscope are congruent.
Solution: True
Q.90. Two acute angles are congruent.
Solution:
False
Since, two acute angles may vary from 0° to 89°. So, two acute angles of different measure are not congruent.
Q.91. Two right angles are congruent.
Solution:
True
Q.92. Two figures are congruent, if they have the same shape.
Solution:
False
Since, two figures are congruent, if they have the same shape and same size.
Q.93. If the areas of two squares is same, they are congruent.
Solution: True
Q.94. If the areas of two rectangles are the same, they are congruent.
Solution: False
Q.95. If the areas of two circles are the same, they are congruent.
Solution: True
Q.96. Two squares having the same perimeter are congruent.
Solution: True
Q.97. Two circles having the same circumference are congruent.
Solution: True
Q.98. If three angles of two triangles are equal, triangles are congruent.
Solution: False
Since, there is no congruency criterion of three angles.
Q.99. If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
Solution: True
Q.100. If two sides and one angle of a triangle are equal to the two sides and angle of another triangle, then the two triangles are congruent.
Solution: False
Since, two triangles are congruent if two sides and included angle of one triangle are equal to the two sides and included angle of another triangle.
Q.101. If two triangles are congruent, then the corresponding angles are equal.
Solution: True
Q.102. If two angles and a side of a triangle are equal to two angles and a side of another triangle, then the triangles are congruent.
Solution: False
If two angles and included side of a triangle are equal to two corresponding angles and the included side of the another triangle, then the triangles are congruent.
Q.103. If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Solution: False
Since, two right triangles are congruent, if hypotenuse and one side of a triangle are equal to hypotenuse and one side of another triangle.
Q.104. If hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.
Solution: True
Since, whenever, hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, we may convert it into ‘two angles and the included side’ form of congruence with the help of angle sum property.
Q.105. AAS congruence criterion is same as ASA congruence criterion.
Solution: False
Q.106. In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then, ∆ABD ≅ ∆ACD by RHS.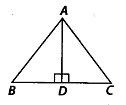 Solution: False
Solution: False
In ∆ABD and ∆ACD,
AD = AD [common]
∠BAD-∠CAD [∵ AD is the bisector of ∠BAC]
∠ADB = ∠ADC [each 90°, ∵ AD ⊥ BC]
∴ ∆ABD ≅ ∆ACD [By ASA criterion]
Q.107. The measure of three angles of a triangle are in the ratio 5 : 3 : 1. Find the measures of these angles.
Solution:
Let the angles of the triangle be 5x, 3x and x.
∴ x + 3x + 5x = 180° [Angle sum property of a triangle]
⇒ 9x = 180°
⇒x=180∘9=20∘
∴ 3x = 3 × 20° = 60°, 5x = 5 × 20° = 100°
Thus, angles of triangle are 100°, 60° and 20°
Q.108. In the given figure, find the value of x. Solution:
Solution: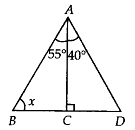 In ∆ABC, ∠ACD = ∠BAC + ∠ABC [Exterior angle property]⇒ 90° = 55° + x⇒ x = 90° – 55° = 35°
In ∆ABC, ∠ACD = ∠BAC + ∠ABC [Exterior angle property]⇒ 90° = 55° + x⇒ x = 90° – 55° = 35°
Thus, x = 35°
Q.109. In the given figure (i) and (ii), find the values of a, b and c.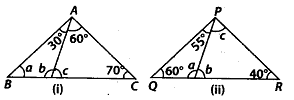 Solution: (i) In ∆ADC, ∠ADB = ∠DAC+ ∠ACD [Exterior angle property]b = 60° +70° = 130° …………(i)
Solution: (i) In ∆ADC, ∠ADB = ∠DAC+ ∠ACD [Exterior angle property]b = 60° +70° = 130° …………(i) Now, in ∆ABD, ∠ABD + ∠ADB + ∠BAD = 180° [Angle sum property]⇒ a + b + 30° = 180°⇒ a = 180° – 30° – 130° (using (1)
Now, in ∆ABD, ∠ABD + ∠ADB + ∠BAD = 180° [Angle sum property]⇒ a + b + 30° = 180°⇒ a = 180° – 30° – 130° (using (1)
⇒ a = 20° ………(ii)
Also, ∠ADC = ∠BAD + ∠ABD [Exterior angle property]
⇒ c = 30° + a
⇒ c = 30° + 20° = 50° [using (ii)]
Thus, a = 20°, b = 130°,c = 50°
(ii) In ∆POS, ∠PSR = ∠SPQ+ ∠PQS [Exterior angle property]
⇒ b = 55° + 60°⇒ b = 115° …………. (i)Now, in ∆PRS, ∠PSR + ∠PRS + ∠SPR = 180° [Angle sum property]
⇒ b + 40° + c = 180°
⇒ c = 180° – 40° – 115° [using (i)]
⇒ c = 25° ………. (ii)
Also, ∠PSQ = ∠SPR + ∠SRP [Exterior angle property]
⇒ a = c + 40°
⇒ a = 25° + 40° = 65° [using (ii)]
Thus, a = 65°, b = 115°, c = 25°
Q.110. In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Yand angle Z is a right angle. Find the measure of ∠Y.
Solution: Given that
∠X = ∠Y + 40° ……….(i)
∠Z = 90° ……….. (ii)
In ∆XYZ
∠X + ∠Y+∠Z = 180° [Angle sum property]
⇒ ∠Y + 30° + ∠Y + 90° = 180° [Using (i) and (ii)]
⇒ 2 ∠Y = 180°- 90° – 30° = 60°
⇒∠Y=60∘2=30∘
Q.111. In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50% less than that of angle C. Find the measure of ∠A.
Solution:
Given that ∠A = ∠B – 40° …………. (i)
and ∠A = ∠C – 50° …………..(ii)
Now, in ∆ABC
∠A + ∠B + ∠C = 180° [Angle sum property]
⇒ ∠A + ∠A + 40° + ∠A + 50° = 180° [Using (i) and (ii)]
⇒ 3∠A + 90° = 180°
⇒ 3∠A = 180° – 90° = 90°
⇒∠A=90∘3=30∘
Q.112. I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
Solution:
A polygon having three sides is a triangle.
Given that the two angles are of measure 15° and 60°
Let third angle of triangle be x.
∴ 15° + 60° + x = 180° [Angle sum property of a triangle]
⇒ x = 180° – 60° – 15°
⇒ x = 105°
Thus, one angle of triangle is obtuse angle. So, triangle is obtuse-angled triangle.
Q.113. Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
Solution:
Let A be the starting point and B be the ending point of Jiya.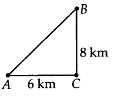
Since ∆ABC is right angled.∴ (AB)2 = (AC)2 + (BC)2
⇒ (AB)2 = 62 + 82 = 36 + 64 = 100
⇒ AB = 10
Thus, Jiya is 10 km away from her starting place.
Q.114. Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Solution: Let ∆BCD be the given rectangular park.
Since, ∆ABC is right angled.∴ (AC)2 = (AB)2 + (BC)2
⇒ (AC)2 = (80)2 + (60)2 = 6400 + 3600 = 10000
⇒ AC = 100 .
∴ Length of route across the park = 100 m and length of route around the edges = (80 + 60) m = 140 m
Thus, the route across the park is shorter than the route around edges of park by
140 m – 100 m = 40 m.
Q.115. In ∆PQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.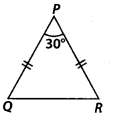 Solution: ∠PRQ ∠PQR [∵ PQ = PR (given)]Now, in ∆POR
Solution: ∠PRQ ∠PQR [∵ PQ = PR (given)]Now, in ∆POR
∠PQR + ∠PRQ+ ∠QPR = 180° [Angle sum property]
⇒ 2∠POR + 30° = 180° [using (1)]
⇒ 2∠PQR = 180° – 30° = 150°
⇒∠PQR=150∘2=75∘
Thus, ∠Q = ∠R = 75°
Q.116. In the given figure, find the measures of angles x and y.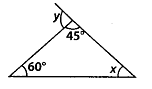 Solution:
Solution: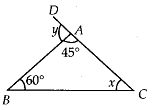 In ∆ABC,∠BAC + ∠ABC + ∠ACB = 180° [Angle sum property]⇒ 45° + 60° + x = 180°
In ∆ABC,∠BAC + ∠ABC + ∠ACB = 180° [Angle sum property]⇒ 45° + 60° + x = 180°
⇒ x = 180°- 45° – 60° = 75° ……………. (i)
Now, ∠BAD =∠ABC + ∠ACB [Exterior angle property]
⇒ y = 60° + x
⇒ y = 60° +75° = 135° [using (i)]
Thus, x = 75° and y = 135°
Q.117. In the given figure, find the measures of ∠PON and ∠NPO.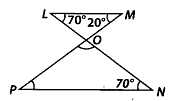 Solution: In ∆LOM,∠LOM + ∠OLM+∠OML = 180° [Angle sum property]
Solution: In ∆LOM,∠LOM + ∠OLM+∠OML = 180° [Angle sum property]
⇒ ∠LOM + 70° + 20° = 180°
⇒ ∠LOM = 180° – 70° – 20° = 90°
∠LOM = ∠PON [Vertically opposite angles]
∴ ∠PON = 90°
Now, in ΔΡΟΝ,
∠PON + ∠ONP + ∠NPO = 180° [Angle sum property]
⇒ 90° + 70° + ∠NPO = 180°
⇒ ∠NPO = 180°- 90° – 70° = 20°
Thus, ∠PON = 90° and ∠NPO = 20°
Q.118. In the given figure QP || RT. Find the values of x and y.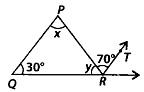 Solution: QP || RT and PR is a transversal.∴ ∠QPR = ∠PRT [Alternate interior angles]
Solution: QP || RT and PR is a transversal.∴ ∠QPR = ∠PRT [Alternate interior angles]
⇒ x = 70°
Now, OP || RT and OR is a transversal.
∴ ∠PQR + ∠QRT = 180° [Co-interior angles]
⇒ 30° + y + 70° = 180°
⇒ y = 180° – 30° – 70° = 80°
Thus, a = 70° and y = 80°,
Q.119. Find the measure of ∠A in the given figure.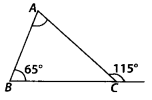 Solution:
Solution: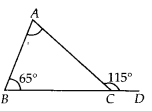
∠ACD = ∠ABC + ∠CAB [Exterior angle property]⇒ 115° = 65° + ∠CAB⇒ ∠CAB = 115° – 65°= 50°
Thus, ∠A = 50°
Q.120. In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
Solution:
Let ∆ABC be the given triangle such that ∠B = 90° and ∠C = 35°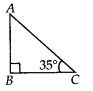
Now, ∠A +∠B + ∠C = 180° [Angle sum property]⇒ ∠A = 180°- 90° – 35°⇒ ∠A = 55°
Thus, third angle of triangle is 55°.
Q.121. Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
Solution: Let ∆ABC be the given isosceles triangle, such that AB = AC and ∠B = ∠C = x.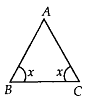
Now, ∠B = ∠C = 4∠A ……….. (i) [given]∠A +∠B +∠C = 180° [Angle sum property]⇒ ∠A + 4 ∠A + 4 ∠A = 180° [Using (i)]
⇒ 9∠A = 180°
⇒∠A=180∘9=20∘
∴ ∠B = ∠C = 4 × 20° = 80°
Thus, 80, 809 and 20° are the angles of the triangle.
Q.122. The angles of a triangle are in the ratio 2 : 3 : 5. Find the angles.
Solution:
Let the angles of the triangle be 2x, 3x and 5x.
∴ 2x + 3x + 5x = 180° [Angle sum property of a triangle]
⇒ 10x = 180°
⇒x=180∘10=18∘
∴ 2x = 2 × 18° = 36°, 3x = 3 × 18° = 54, 5x = 5 × 18°= 90°
Thus, 36°, 54° and 90°are the angles of the triangle.
Q.123. If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°
Solution: Let AABC be the given triangle and BD, CE, AF are the produced side in order.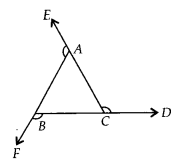
∠ACD = ∠CAB + ∠CBA ………. (i) [Exterior angle property]∠BAE = ∠ABC + ∠ACB ……… (ii) [Exterior angle property]∠CBF = ∠BAC + ∠BCA ……….(iii) [Exterior angle property]
Adding (i), (ii) and (iii), we get
∠ACD + ∠BAE +∠CBF = ∠CAB +∠CBA + ∠ABC + ∠ACB + ∠BAC + ∠BCA
⇒∠ACD + ∠BAE + ∠CBF
= 2[∠ABC + ∠ACB + ∠BAC]
= 2(180°) [Angle sum property]
= 360°
Q.124. In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
Solution:
∠ABX=∠BAC + ∠BCA [Exterior angle property]
⇒ 140° =2∠BAC [∵ ∠A = ∠C]
∠BAC=140∘2=70∘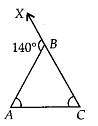
∴ BAC =∠BCA = 70° ……… (i)Now, in ∆ABC∠A +∠B + ∠C = 180° [Angle sum property]
⇒ ∠B = 180° – 70° -70 [using (i)]
⇒ ∠B = 40°
Thus, ∠A = 70°, ∠B = 40° and ∠C = 70° are the angles of triangle.
Q.125. Find the values of x and y in the given figure. Solution: In ∆QRS, ∠QST = ∠QRS + ∠SOR [Exterior angle property]
Solution: In ∆QRS, ∠QST = ∠QRS + ∠SOR [Exterior angle property]
⇒ x = 30° + 50° = 80°
Also, in ∆QRT, ∠PQT = ∠QRT + ∠QTR [Exterior angle property]
⇒ y = 30° + 45° = 75°
Thus, x = 80° and y = 75°
Q.126. Find the value of x in the given figure.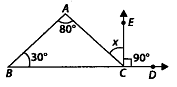 Solution: In ∆ABC, ∠ACD= ∠CAB + ∠CBA [Exterior angle property]⇒ x + 90° = 80° + 30°
Solution: In ∆ABC, ∠ACD= ∠CAB + ∠CBA [Exterior angle property]⇒ x + 90° = 80° + 30°
⇒ x = 110°- 90° = 20°
Q.127. The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10, find the three angles.
Solution: Let ∆ABC be the given triangle and descending order of angles of the triangle is ∠A, ∠B, ∠C
Now, ∠A – ∠B = 10° ………..(i)
∠B – ∠C = 10° ……….. (ii)
Also, ∠A +∠B + ∠C = 180° [Angle sum property]
⇒ ∠B + 10° + ∠B + ∠B – 10° = 180° [Using (i) and (ii)]
⇒ 3∠B = 180°
⇒∠B=180∘3=60∘
∴∠A = ∠B + 10° = 60° + 10° = 70°
and ∠C = ∠B – 10° = 60° – 10° = 50°
Thus, 70°, 60° and 50° are the angles of the triangle.
Q.128. In ∆ABC, DE || BC (see figure). Find the values of x,y and z.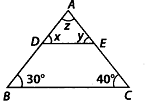 Solution:
Solution:
DE || BC and AB is a transversal.∴ ∠ADE = ∠DBC [Corresponding angles]
⇒ x= 30°
Now, DE || BC and AC is a transversal.
∴ ∠AED = ∠ECB [Corresponding angles]
⇒ y = 40°
In ∆ABC,
∠A + ∠B + ∠C = 180° [Angle sum property]
⇒ z + 30° + 40° = 180°
⇒ z = 180° – 40° – 30° = 110°
Thus, x = 30°, y = 40° and z = 110°.
Q.129. In the given figure, find the values of x, y and z.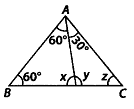 Solution: In ∆ABD,∠BAD + ∠BDA + ∠ABD = 180° [Angle sum property]
Solution: In ∆ABD,∠BAD + ∠BDA + ∠ABD = 180° [Angle sum property]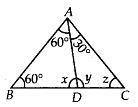
⇒ 60° + x + 60° = 180°⇒ x = 180° – 120° = 60°Now, ∠ADC = ∠BAD + ∠ABD [Exterior angle property]
⇒ y = 60° + 60° = 120°
Also, in ∆ADC,
∠ADB – ∠DAC + ∠DCA [Exterior angle property]
⇒ x = 30° + z
⇒ z = 60° – 30° = 30° [∵ x = 60°]
Thus, x = 60°, y = 120° and z = 30°
Q.130. If one angle of a triangle is 60° and the other two angles are in the ratio 1 : 2, find the angles.
Solution: Let ∆ABC be the given triangle such that ∠A = 60° and let angle B and C are x and 2x respectively.
∠A + ∠B + ∠C = 180° [Angle sum property]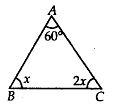
⇒ 60° + x + 2x = 180°⇒ 3x = 180° – 60° = 120°⇒x=120∘3=40∘
∴ ∠B = 40° and ∠C = 2 × 40° = 80°
Q.131. In ∆POR, If 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
Solution: In ∆POR,
∠P + ∠Q+ ∠R = 180° [Angle sum property]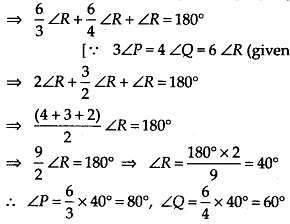
Thus, ∠P = 80°, ∠Q = 60° and ∠R = 40°
Q.132. In ∆DEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find
(i) ∠F
(ii) ∠EOF
Solution:
(i) In ∆DEF,
∠D + ∠E +∠F = 180° [Angle sum property]
⇒ 60° +70° + ∠F = 180°
⇒ ∠F = 180° – 60° – 70°= 50°
(ii) Since, EO and FO are the bisectors of ∠E and ∠F respectively.
∴ ∠OEF=∠OED=70∘2=35∘
and ∠OFE=∠OFD=50∘2=25∘
Now, in ∆OEF, ∠
OEF + ∠OFE+ ∠EOF = 180° [Angle sum property]
⇒ 35° + 25° + ∠EOF = 180°
⇒ ∠EOF = 180° – 35° – 25° = 120°
Q.133. In the given figure, ∆PQR is right-angled at P.U and Tare the points on line QRF. If OP || ST and US || RP, find ∠S.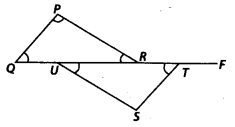
Solution:QP || ST and QT is a transversal.∴ ∠PQT = ∠STO [Alternate interior angles]
US || PR and UR is a transversal.
∴ ∠PRU = ∠SUR [Alternate interior angles]
Two angles of ∆PQR equal to two angles of ∆STU. Therefore, third angle also will be equal.
∴ ∠QPR = ∠TSU
Now, given that ∠P = 90°
∴ ∠S = 90°.
Q.134. In each of the given pairs of triangles of figure, applying only ASA congruence criterion, determine which triangles are congruent. Also, write the congruent triangles in symbolic form.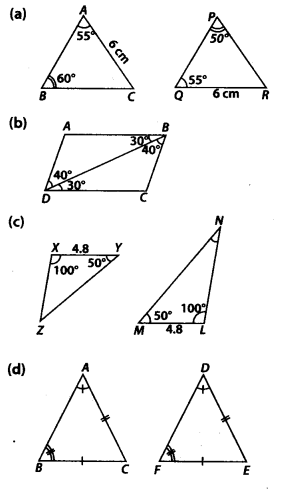
Solution: (a) In the given figure, ∆ABC and ∆POR are not congruent.(b) In ∆ABD and ∆CDB,
BD = DB (common)
∠ABD =∠CDB = 30° (given)
∠ADB = ∠CBD = 40° (given)
∴ ∆ABD ≅ ∆CDB (ASA criterion)
(c) In ∆XYZ and ∆LMN,
XY = LM = 4.8 (given)
∠YXZ = ∠MLN – 100° (given)
∠XYZ = LMN = 50° (given)
∴ ∆XYZ ≅ ∆LMN (ASA criterion)
(d) In ∆ABC and ∆DFE,
∠A =∠D (given)
∠B = ∠F (given)
∴∠C = ∠E (since two angles are equal)
BC = FE (given)
∴ ∆ABC ≅ ∆DFE (ASA criterion)
(e) In ∆PON and ∆MNO,
NO = ON (common)
∠NOP = ∠ONM = 50° + 40 = 90° (given)
∠ONP = ∠NOM = 50° (given)
∴ ∆PON ≅ ∆MNO (ASA criterion)
(f) In ∆AOD and ∆BOC,
∠AOD = ∠BOC (Vertically opposite angles)
OD = OC (given)
∠ADO = ∠BCO (given)
∴ ∆AOD ≅ ∆BOC (ASA criterion)
Q.135. In each of the given pairs of triangles of figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In case of congruence, write the result in symbolic form: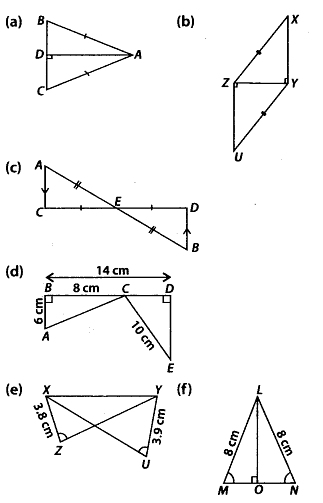
Solution:(a) In ∆ADB and ∆ADC,AD = AD (common)
∠ADB = ∠ADC (Each 90°)
AB = AC (given hypotenuse)
∴ ∆ADB ≅ ∆ADC (RHS criterion)
(b) In ∆XYZ and ∆UZY,
∠Y = ∠Z (Each 90°)
XZ = UY (given hypotenuse)
YZ = ZY (common)
∴ ∆XYZ ≅ ∆UZY (RHS criterion)
(c) In ∆ACE and ∆BDE,
∠ACE = ∠BDE (AC || BD, alternate interior angles)
CE = DE (given)
∠AEC = ∠BED (Vertically opposite angles)
∴ ∆ACE ≅ ∆BDE (ASA criterion)
∴ Triangles are congruent but not by RHS congruence criterion
(d) In ∆ABC, by phythagoras theorem
(AC)2 = (AB)2 + (BC)2
= 62 + 82 = 36 + 64 = 100 = 102
∴ AC – 10 cm
In ∆EDC,
DC = BD – BC = (14 – 8) cm = 6cm, CE = 10 cm
Now, in ∆ABC and ∆CDE,
∠B =∠D (each 90°)
AB = CD = 6 cm
AC = CE = 10 cm (hypotenuse)
∴ ∆ABC ≅ ∆CDE (RHS criterion)
(e) In the given figure, ∆XYZ and ∆YXU are not congruent by any criterion.
(f) In ∆LMO and ∆LNO,
LO = LO (common)
LM = LN = 8 cm (hypotenuse)
∠LOM = ∠LON (each 90°)
∴ ∆LOM ≅ ∆LON (RHS criterion)
Q.136. In the given figure, if RP=RQ, find the value of x.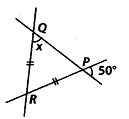 Solution:
Solution:
RP = RQ∴ ∠RQP = ∠RPQ = x [angles opposite to equal sides are equal]
Now, ∠RPQ = 50° [vertically opposite angles]
∴ x = 50°
Q.137. In the given figure, if ST = SU, then find the values of x and y.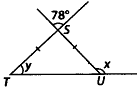 Solution:
Solution:
∠TSU = 78° [vertically opposite angles]∠SUT = ∠STU = y [∵ ST = SU]
Now, in ∆STU,
∠STU + ∠SUT + ∠TSU = 180° [Angle sum property]
⇒ y + y + 78° = 180°
⇒ 2y = 180° – 78° = 102°
⇒y=102∘2=51∘
Now, x = ∠TSU + ∠UTS [Exterior angle property]
⇒ x = 78° + 51°
⇒ x = 129°
Thus, x = 129° and y = 51°,
Q.138. Check whether the following measures (in cm) can be the sides of a right-angled triangle or not. 1.5, 3.6, 3.9
Solution:
Here, (1.5)2 + (3.6)2 = 2.25 + 12.96 = 15.21 and (3.9)2 = 15.21
Thus, (1.5)2 + (3.6)2 = (3.9)2
Yes, given sides are sides of a right angled triangle.
Q.139. Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Solution: Let AB be the given pole of height 8m and rope be AC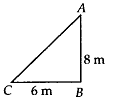
Since, ∆ABC is a right angled triangle.∴ (AC)2 = (AB)2 + (BC)2
(AC)2 = 82 + 62 = 64 + 36
(AC)2 = 100 = 102
∴ AC = 10 m
Thus, the required length of rope is 10 m.
Q.140. In the given figure, if y is five times x, find the value of z.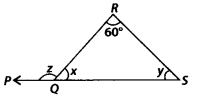 Solution: In ∆QRS,∠ROS + ∠RSQ + ∠QRS = 180° [Angle sum property]
Solution: In ∆QRS,∠ROS + ∠RSQ + ∠QRS = 180° [Angle sum property]
⇒ x + y + 60° = 180°
⇒ x + 5x = 180° – 60° [∵ y = 5x (given)]
⇒ 6x = 120°
⇒x=120∘6=20∘
∴ y = 5x = 5 × 20° – 100°
Now, ∠RQP = ∠QRS + ∠QSR [Exterior angle property]
z = 60° + 100° = 160°
Q.141. The lengths of two sides of an isosceles triangle are 9 cm and 20 cm. What is the perimeter of the triangle? Give reason.
Solution:
Sides of isosceles triangle are 9 cm and 20 cm.
Since, sum of any two sides of a triangle is greater than third side.
If third side will be 9 cm then 9 + 9 = 18 < 20
So, the triangle will not form.
∴ Third side of triangle must be 20 cm.
Perimeter = (9 + 20 + 20) cm = 49 cm.
Q.142. Without drawing the triangles write all six pairs of equal measures in each of the following pairs of congruent triangles.
(a) ∆STU ≅ ∆DEF
(b) ∆ABC ≅ ∆LMN
(c) ∆YZX ≅ ∆POR
(d) ∆XYZ ≅ ∆MLN
Solution:
(a) ∆STU ≅ ∆DEF
ST = DE, TU= LF, SU = DF
∠STU = ∠DEF, ∠SUT = ∠DFE, ∠TSU = ∠EDF
(b) ∆ABC ≅ ∆LMN
AB = LM, BC = MN, AC = LN
∠ABC = ∠LMN, ∠ACB = ANM, ∠BAC =∠MLN
(c) ∆YZX ≅ ∆POR
YZ = PQ, ZX = OR, YX = PR
∠YZX=∠POR, ∠YXZ = ∠PRO, ∠XYZ = ∠RPQ
(d) ∆XYZ ≅ ∆MLN
XY = ML, YZ = LN, XZ = MN
∠XYZ = ∠MLN, ∠XZY = ∠MNL, ∠ZXY = ∠NML.
Q.143. In the following pairs of triangles of figure, the lengths of the sides are indicated along the sides. By applying SSS congruence criterion, determine which triangles are congruent. If congruent, write the results in symbolic form.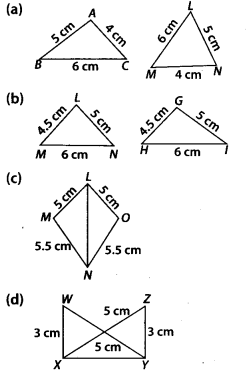
Solution: (a) In ∆ABC and ∆NLM,AB = NL = 5 cm (given)
BC = LM = 6 cm (given)
AC = NM = 4 cm (given)
∴ ∆ABC ≅ ∆NLM (SSS criterion)
(b) In ∆LMN and ∆GHI,
LM = GH = 4.5 cm (given)
LN = GI = 5 cm (given)
MN = HI = 6 cm (given)
∴ ∆LMN ≅ ∆GHI (SSS criterion)
(c) In ∆LMN and ∆LON,
LM = LO = 5 cm (given)
MN = ON = 5.5 cm (given)
LN = LN (common)
∴ ∆LMN ≅ ∆LON (SSS criterion)
(d) In ∆XYZ and ∆YXW,
XY = YX (common)
ZY = WX = 3 cm (given)
ZX = WY = 5 cm (given)
∴ ∆YXW ≅ ∆XYZ (SSS criterion)
(e) In ∆AOB and ∆DOE,
AO = DO = 2 cm (given)
AB = DE = 2 cm (given)
BO = EO = 1.5 cm (given)
∴ ∆AOB ≅ ∆DOE (SSS criterion)
(f) In ∆STU and ∆SVU,
SU = SU (common)
ST = SV = 5 cm (given)
UT = UV = 3 cm (given)
∴ ∆STU ≅ ∆SVU (SSS criterion)
(g) In ∆PQR and ∆RSP,
PR = RP (common)
PQ = RS = 5 cm (given)
OR = SP = 3 cm (given)
∴ ∆PQR ≅ ∆RSP (SSS criterion)
(h) In ∆STU, by Pythagoras theorem,
TU2 = (10.5)2 – 52 = 135.25
and in ∆PQR, QR2 = (10.5)2 – 52 = 135.25
∴ TU2 = QR2 ⇒ TU = QR …….. (i)
In ∆STU and ∆POR,
ST = PQ = 5 cm (given)
SU = PR = 10.5 cm (given)
TU = QR (From (1) .
∆STU ≅ ∆PQR (SSS criterion)
Q.144. ABC is an isosceles triangle with AB = AC and D is the mid-point of base BC (see figure).
(a) State three pairs of equal parts in the triangles ABD and ACD.
(b) Is AABD AACD. If so why?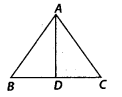 Solution: (a) In ∆ABD and ∆ACD,AD = AD (common)
Solution: (a) In ∆ABD and ∆ACD,AD = AD (common)
AB = AC (given)
BD = CD (D is mid-point of BC)
(b) Yes, by using (a) part, we get
∆ABD ≅ ∆ACD (SSS criterion)
Q.145. In the given figure, it is given that LM = ON and NL = MO
(a) State the three pairs of equal parts in the triangles NOM and MLN.
(b) Is ∆NOM ≅ ∆MLN.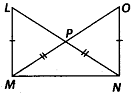 Give reason.
Give reason.
Solution: (a) In ∆NOM and ∆MLN,
NM = MN (common)
OM = LN (given)
ON = LM (given)
(b) Yes, by using part (a), we get
∆NOM ≅ ∆MLN (SSS criterion)
Q.146. Triangles DEF and LMN are both isosceles with DE = DF and LM = LN, respectively. If DE = LM and EF = MN, then, are the two triangles congruent? Which condition do you use? If ∠E = 40°, what is the measure of ∠N?
Solution: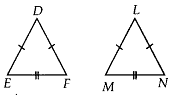 In ∆DEF and ∆LMN,EF = MN (given)DE = LM given
In ∆DEF and ∆LMN,EF = MN (given)DE = LM given
DF = LN [∵ DE = DF and LM = LN]
∴ ∆DEF ≅ ∆LMN (SSS criterion)
∴ ∠E = ∠M [By C.P.C.T.)
Now, ∠E = 40° ⇒ ∠M = 40°
Since, ∠M = ∠N [∵ LN = LM]
∴ ∠N = 40°
Q.147. If APQR and ASOR are both isosceles triangle on a common base OR such that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent? Which condition do you use?
Solution: Let ∆PQR and ∆SOR are the given triangles such that PQ = PR and SQ = SR.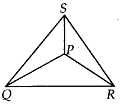
Now, in ∆PSQ and ∆PSR,PQ = PR (given)SQ = SR (given)
PS = PS (common)
∴ ∆PSQ ≅ ∆PSR (SSS criterion)
Yes, the ∆PSQ and ∆PSR are congruent by using SSS criterion
Q.148. In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
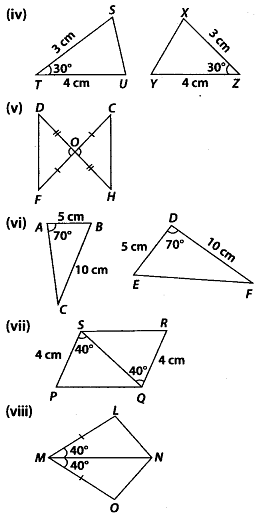
Solution:(i) In ∆POR and ∆TUS,PQ = TU = 3 cm (given)
OR = US = 5.5 cm (given)
∠POR = ∠TUS = 40° (given)
∴ ∆POR ≅ ∆TUS (SAS criterion)
(ii) In the given figure, ∆JKL and ∆MNO are not congruent by any criterion.
(iii) In ∆ABE and ∆CBD,
∠EAB = ∠DCB = 50° (given)
AE = CD = 5 cm (given)
AB = CB = 5.2 cm (given)
∴∆ABE ≅ ∆CBD (SAS criterion)
(iv) In ∆SUT and ∆XYZ
ST = XZ = 3 cm (given)
UT = YZ = 4 cm (given)
∠STU = ∠XZY = 30° (given)
∴ ∆SUT ≅ ∆XYZ (SAS criterion)
(v) In ∆DOF and ∆HOC,
DO = HO (given)
FO = CO (given)
∠DOF = ∠HOC (Vertically opposite angles)
∴ADOF ≅ AHOC (SAS criterion)
(vi) In the given figure, ∆ABC and ∆DEF are not congruent by any criterion.
(vii) In ∆PSQ and ∆RQS.
SQ = QS (common)
PS = RQ = 4 cm (given)
∠PSQ = ∠RQS = 40° (given)
∴ ∆PSQ ≅ ∆ROS (SAS criterion)
(viii) In ∆LMN and ∆OMN,
MN = MN (common)
LM = OM (given)
∠LMN = ∠OMN = 40° (given)
∴ ∆LMN ≅ ∆OMN (SAS criterion)
Q.149. State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
(a) ∆POR : PQ = 3.5 cm, OR = 4.0 cm, ∠Q=60°
∆STU : ST = 3.5 cm, TU= 4 cm, ∠T = 60°
(b) ∆ABC : AB = 4.8 cm, ∠A = 90°, AC = 6.8 cm
∆XYZ : YZ = 6.8 cm, ∠X = 90°, ZX = 4.8 cm
Solution:
(a)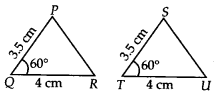
In ∆PQR and ∆STU,PQ = ST = 3.5 cm (given)∠PQR = ∠STU = 60° (given)
OR = TU = 4 cm (given)
∴ ∆PQR ≅ ∆STU (SAS criterion)
(b) Here, ∆ABC and ∆XYZ are not congruent by any criterion.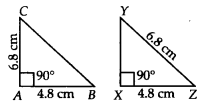
Q.150. In the given figure, PO = PS and ∠1 = ∠2.
(i) Is ∆POR = ∆PSR? Give reasons.
(ii) Is QR = SR? Give reasons.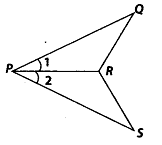 Solution:(i) In ∆PQR and ∆PSR,PQ = PS (given)
Solution:(i) In ∆PQR and ∆PSR,PQ = PS (given)
∠1 = ∠2 (given)
PR = PR (common)
∴ ∆POR ≅ ∆PSR (SAS criterion)
(ii) Yes, QR = SR (By C.P.C.T.)
Q.151. In the given figure, DE = IH, EG = FI and ∠E = 21. Is ∆DEF ≅ ∆HIG? If yes, by which congruence criterion?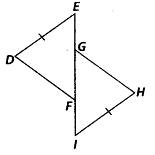
Solution: In ∆DEF and ∆HIG,DE = HI (given)
∠E = ∠I (given)
EF = IG ∴ ∆DEF ≅ ∆HIG (SAS criterion)
∴ ∆DEF ≅ ∆HIG (SAS criterion)
Q.152. In the given figure, ∠1 = ∠2 and ∠3 = ∠4.
(i) Is ∆ADC ≅ ∆ABC? Why?
(ii) Show that AD = AB and CD = CB.
Solution: (i) In ∆ADC and ∆ABC,∠1 = ∠2 (given)
AC = AC (common)
∠3 = ∠4 (given)
∴ ∆ADC = ∆ABC (ASA criterion)
(ii) By using (i) part, we get
AD = AB (By C.P.C.T.)
and CD = CB (By C.P.C.T.)
Q.153. Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.
(i) Is ∆ABC = ∆DCB? Why?
(ii) Is AB = DC? Why?
(iii) Is AC = DB? Why?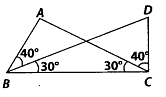
Solution: (i) In ∆ABC and ∆DCB,∠ABC = ∠DCB = 40° + 30 = 70° (given)
∠ACB = ∠DBC = 30° (given)
BC = CB (common)
∴ ∆ABC ≅ ∆DCB (ASA criterion)
(ii) Yes, by using (1) part, we get
AB = DC (By C.P.C.T.)
(iii) Yes, by using (1) part, we get
AC = DB (By C.P.C.T.)
Q.154. In the given figure, OS ⊥ PR, RT ⊥ PQ and QS = RT.
(i) Is ∆QSR = ∆RTO? Give reasons.
(ii) Is ∠PQR = ∠PRQ? Give reasons.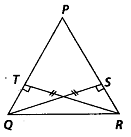
Solution: (i) In ∆QSR and ∆RTO,∠OSR = ∠RTO = 90° (∵ QS ⊥ PR and RT ⊥ PQ (given))
QS = RT (given)
QR = RO (common hypotenuse)
∴ ∆QSR ≅ ∆RTQ (RHS criterion)
(ii) Yes, by using (1) part, we get
∠TQR = ∠SRQ (By C.P.C.T)
⇒ ∠PQR = PRQ
Q.155. Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.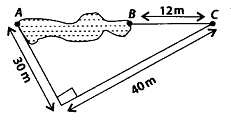
Solution:
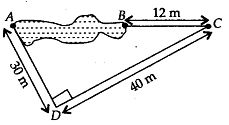 Since, ∆ADC is right-angled triangle∴ (AC)2 = (AD)2 + (CD)2
Since, ∆ADC is right-angled triangle∴ (AC)2 = (AD)2 + (CD)2
= (30)2 + (40)2 = 900 + 1600 = 2500 = (50)2
∴ AC = 50 m
Now, AB = AC – BC = 50 – 12 = 38
Thus, the distance AB is 38 m.
Q.156. Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
Solution:
Let AB and CD are the given poles of heights 15 m and 10 m such that AC = 13 m.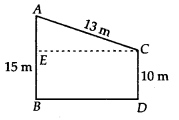
Now, BD = CE and BE = CD = 10 m∴ AE = AB – BE = (15 – 10) m = 5 mNow, in ΔAEC,
(AC)2 = (AE)2 + (EC)2
⇒ (13)2 = 52 + (EC) 2
⇒ (EC)2 = 169 – 25 = 144 – (12)2
∴ EC = 12 m
Also, BD – 12 m
Thus, distance between the feet of poles is 12 m.
Q.157. The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground,
(a) Find the length of the ladder.
(b) If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
Solution: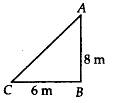
(a) Let AC be the given ladder such that BC = 6 m and AB = 8 mNow, in ΔABC,(AC)2 = (AB)2 + (BC)2
= 82 + 62
= 64 + 36 = 100 = (10)2
∴ AC = 10 m
Thus, length of the ladder is 10 m.
(b) Let AC be the ladder of length 10 m and BC = 8 m.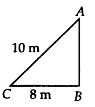 In ΔABC,(AC)2 = (AB)2 + (BC)2
In ΔABC,(AC)2 = (AB)2 + (BC)2
⇒ (10)2 = (AB)2 + (8)2
⇒ (AB)2 = 100 – 64 = 36 = (6)2
∴ AB = 6 m
Thus, the ladder top reaches 6 m above the ground.
Q.158. In the given figure, state the three pairs of equal parts in ΔABC and ΔEOD. Is ΔABC = ΔEOD? Why?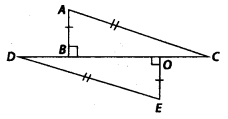 Solution: In ΔABC and ΔEOD,AB = EO (given)
Solution: In ΔABC and ΔEOD,AB = EO (given)
∠ABC = ∠EOD = 90° (given)
AC = ED (given hypotenuse)
∴ AABC ≅ AEOD (RHS criterion)
|
76 videos|344 docs|39 tests
|
FAQs on NCERT Exemplar Solutions: Triangles - Mathematics (Maths) Class 7
| 1. How to find the perimeter of a triangle? |  |
| 2. What is the Pythagorean theorem and how is it used in triangles? |  |
| 3. How do you determine if a triangle is equilateral, isosceles, or scalene? |  |
| 4. What is the sum of the interior angles of a triangle? |  |
| 5. How do you calculate the area of a triangle? |  |

|
Explore Courses for Class 7 exam
|

|


















