Nuclear Reaction: Assignment | Modern Physics PDF Download
Q.1. A nucleus at rest undergoes a decay emitting an α - particle of de-Broglie wavelength λ = 5.76 x 10-15 m. If the mass of the daughter nucleus is 223.610 amu and that of the α - particle is 4.002 amu , determine the total kinetic energy in the final state. Hence, obtain the mass of the parent nucleus in amu.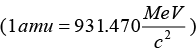
Let ZX4 represent the parent nucleus. The parent nucleus decays emitting α - particles
∴ ZX4 → Z-2 YA-4 + 2He4Mass of daughter nucleus Y = 223.610 amu , Mass of α - particle = 4.002 amu
De-Broglie wavelength of α - particle, λ = 5.76 x 10-15 m
So, momentum of α - particle would beFrom law of conservation of linear momentum, this should also be equal to the linear momentum the daughter nucleus thus pα = pY
Let Kα and KY be the kinetic energies of α - particle and daughter nucleus. Then total kinetic energy in the final state is∵ 1 amu 1.67x10-27 kg
Mass equivalent to energy
or Δm = 0.0067amu ∴ mX = mY + mα + Δm
or mX = (223.610 + 4.002 + 0.0067)amu or mX = 227.67∴ Mass of parent nucleus = 227.62 amu
Q.2. A nucleus with mass number 220 initially at rest emits an α - particle. If the Q value of the reaction is 5.5 MeV , calculate the kinetic energy of the α - particle
Linear momentum is conserved.
∴ p1 = p2
butwhere K = kinetic energy
where K2 is for α - particle and K1 is for nucleus.
or 216K1 = 4K2 or K2 = 54K1 ....(i)
Given: K1 + K2 = 5.5MeV .....(ii)From (i) and (ii),
K1 + 54K1 = 5.5 (MeV)
or 55K1 = 5.5 (MeV)
∴ K254 x K1 oror K2 = 5.4 MeV ....(iv)
∴ Kinetic energy of α - particle = 5.4 MeV
Q.3. In a nuclear reaction 235U undergoes fission liberating 200 MeV of energy. The reactor has 10% efficiency and produces 1000MW power. If the reactor is to function for 10 year, find the total mass of uranium required.
∴ Equivalent energy = Power input x time = 1010 x 365 x 24 x 60 x 60 J
= 31.1536 x 1018 J ...(i)Now 1 fission releases 200 MeV energy
∴ 1 fission releases energy = 200 x 1.6 x 10-13 J (ii)From (i) and (ii),
or Number of fissions = 9.85 x 1028
∴ Number of U235 atoms = 9.85 x 1028
Avogadro number 6.02 x 1026 per kg 26∴ 6.02 x 106 atoms are contained in 235kg of U235
∴ 9.85 x 1028 atoms are contained in mass
∴ Mass of U235 = 38451kg
Q.4. If a star can convert all the He nuclei completely into oxygen nuclei, then find the energy released per oxygen nuclei. [Mass of He nucleus is 4.0026 amu and mass of oxygen nucleus is 15.9994 amu]
4[2He4] →8 O16
Binding energy Δm x 931.5 MeV = (4 x 4.0026 -15.9994) x 931.5 MeV = 10.24MeV
∴ Energy released per oxygen nuclei = 10.24 MeV
Q.5. The element Curium 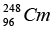 has a mean life of 1013 second, its primary decay modes are spontaneous fission and α-decay, the former with a probability of 8% and the latter with a probability of 92%. Each fission releases 200 MeV of energy. The masses involved in α-decay are as follows:
has a mean life of 1013 second, its primary decay modes are spontaneous fission and α-decay, the former with a probability of 8% and the latter with a probability of 92%. Each fission releases 200 MeV of energy. The masses involved in α-decay are as follows: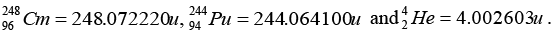
Calculate the power output from a sample of 1020Cm atoms.
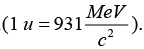
The primary decay modes of 96Cm248 are
(i) Spontaneous fission (probability 8%)
(ii) - α decay (probability 92%).The nuclear reaction is given as:
96Cm248 → 94Pu244 + 2He4∴ Mass defect in the reaction = Δm
∴ Δm = mass of Cm - mass of Pu - mass of He
or Δm = 248.072220 - 244.064100 - 4.002603 or Δm = 0.005517u∴ Energy released = (0.00515 x 931) MeV
Eα = 5.136 MeV
Given: = Ef Each fission released 200 meV of energyMean life of 1013 sec
again dN/dt = λN where N is given to be 1020
∴ Rate of decay = (10-13)(1020) or Rate of decay 107 dps
of these dps 107 dps, 8% are in fission and 92% are in α - decay process.
Energy released per second due to fission
Energy released per sec due to α - decay
Total energy released per second = (16 + 4.725)107 MeV = 20.725 x 107 MeV
∴ Power output = Energy per second
= (20.725 x 107) x (1.6 x 10-13)J / s = 3.316 x 10-5 W = 3.32 x 10-5 W
Q.6. A star initially has 1040 deuterons. It produces energy via the processes
1H2 + 1H2 → 1H3 + p, and 1H2 + 1H2 →2 He4 + n.
If the average power radiated by the star is 1016W , then the time required for the deuteron supply of the star to be exhausted.
The masses of the nuclei are as follow:
M(H2) = 2.014 amu ; M(p) = 1.007 amu; M (n) = 1.008 amu; M (He4) = 4.001amu.
1H2 + 1H2 → 1H3 + p, and 1H2 + 1H2 →2 He4 + n.
by adding 3(1H2) → 2He4 + p + n
∴ Δm = 3(2.014) - [4.001 + 1.007 + 1.008] or Δm = 0.026 amu
Mass is converted into energy1 amu = 931.5 MeV or 1 amu = 931.5 x 106 x 1.6 x 10-19 J
∴ Energy from (Δm) = 0.026 x 931.5 x 1.6 x 10-13 J = 3.87 x 10-12 J
∴ Energy released by 3 deuterons = 3.87 x 10-12 J∴ Energy for 1040 deuterons
Time is of the order of 1012 sec.
Q.7. A nucleus X , initially at rest, undergoes alpha decay according to the equation,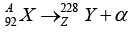
(a) Find the values of A and Z in the above process.
(b) The alpha particle produced in the above process is found: to move in a circular track. of radius 0.11 m in a uniform magnetic field of 3 tesla. Find the energy (in MeV) released during the process and the binding energy of the parent nucleus X .
Given that: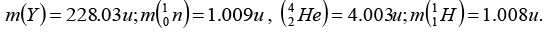
(a) A = 228 + 4 = 232, Z = 92 - 2 = 90
(b) The magnetic force q vB provides centripetal force mv2/r to α - particle for its circular motion.
Linear momentum is conserved in the process.
mYvY = mαvα ....(ii)
Nucleus X is initially at rest
Total kinetic energy = Ka + Kr
Equivalent mass = 5.31/931.5 = 0.0057amu
X is parent nucleus, Y is daughter nucleusAlso mX = mY + mα + equivalent mass
= 228.03 + 4.003 + 0.0057 = 232.0387 amuNow, Nucleons = 92 protons + 140 neutron
Binding energy = (92 x 1.008) + (140 x 1.009) - 232.0387
B.E. = 1.9573amu or B.E. = 1.9573 x 931.5 MeV
∴ B.E. of nucleus X = 1823MeV ...(iv)
Q.8. It is proposed to use the nuclear fusion reaction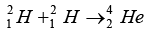
in a nuclear reactor of 200 MW rating. If the energy from the above reaction is used with 25 percent efficiency in the reactor, how many gram of deuterium fuel will be needed per day. (The masses 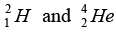 are 2.0141 atomic mass unit and 4.0026 atomic mass unit respectively).
are 2.0141 atomic mass unit and 4.0026 atomic mass unit respectively).
Deuterium fuel needed per day in the reactor:
Mass defect provides the energy in the reactor:Δm = 2(2.0141) - (4.0026) = 4.0282 - 4.0026 = 0.0256amu
∴ ΔE (m)(931.5 MeV) (0.0256)(931.5)x1.6x10-13 J = 3.82x10-12 J
Efficiency = 25%
∴ Energy available due to fusion of two deuterium nuclei
∴ Energy available = 9.55 x 10-13 J
Energy available per deuterium nuclei
Total energy needed = power x time = (200 x 106) x (24 x 60 x 60) = 1.728x1013 J
Number of deuterium nuclei required∴ Mass of deuterium required = m
or Mass = 120.26gram
Hence 120.26 gram of deuterium fuel will be needed per day in the nuc1ear reactor
|
37 videos|16 docs|19 tests
|
FAQs on Nuclear Reaction: Assignment - Modern Physics
| 1. What is a nuclear reaction? |  |
| 2. What is the significance of nuclear reactions? |  |
| 3. How do nuclear reactions occur? |  |
| 4. What is the difference between nuclear fusion and nuclear fission? |  |
| 5. Are nuclear reactions safe? |  |

|
Explore Courses for Physics exam
|

|





 where K = kinetic energy
where K = kinetic energy

 or K2 = 5.4 MeV ....(iv)
or K2 = 5.4 MeV ....(iv)


































