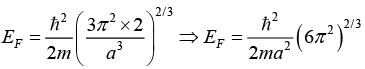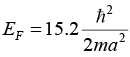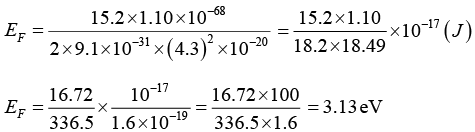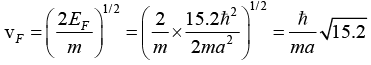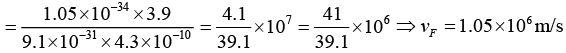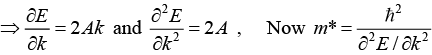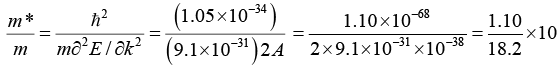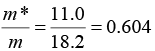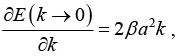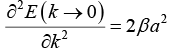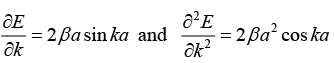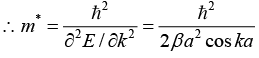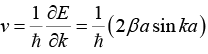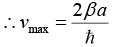Einstein & Debye Theory of Specific Heat: Assignment | Solid State Physics, Devices & Electronics PDF Download
Q.1. Debye temperature (θD) for a Na metal is 150 K . Find its molar-specific heat at 10 K.
Debye T3 - law is
Q.2. At very low temperatures, the specific heat of a rock salt varies with the temperature as CV = A(T/θD)3 where A = 464 cal mol-1K-1 and θD = 281K. How much heat is required to raise the temperature of n = 2 moles of rock salt from 10 to 50 K?
Heat required is
Q.3. At low temperatures, the Debye temperature (θD) for a NaCl and a KCl , which have the same crystal structure, are 330 K and 220 K respectively. The lattice specific heat of KCl at 5K is 3.8 x 10-2 J/mol-K. Estimate the lattice specific heat of NaCl at 10 K.
Q.4. Potassium has the bcc structure with lattice constant 5.3Å. Calculate the Debye temperature on the assumption that the transverse and longitudinal elastic waves in potassium have the same velocity c = 1.5 km/s.
Taking cl = ct = c, we have
Now V/N = a3/2 for bcc
Nowor
Q.5. At a very low temperatures, the specific heat of a rock salt varies with the temperature according to the Debye T3 law, 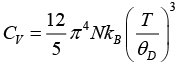 where θD for rock salt is 281 K . How much heat is required to raise the temperature of the 2 k-mol of the rock salt from 10 to 50 K?
where θD for rock salt is 281 K . How much heat is required to raise the temperature of the 2 k-mol of the rock salt from 10 to 50 K?
Given θD = 281K, m = 2k-mol, T1 = 10K, T2 = 50K, Q = ?
Debye T3, law is given as
Since the specific heat varies as T3, the calculation must be made by considering the different range of temperatures. Let the ranges of temperatures in 0K be 10 - 20, 20 - 30, 30 - 40 and 40 - 50
The rise of the temperature in each case is 10K. Then mean temperatures are: 15, 25, 35 and 45K. Therefore, the quantity of heat required to raise the temperature of the 2 k-mol of the salt through 10K is given by
Q.6. Diamond (atomic weight of the carbon = 12 amu) has young’s modulus of 1012 Nm-2 and a density of 3500 Kg/m3. Compute the Debye temperature for the diamond.
Given; Atomic Weight of C = 12 amu, Y = 1012 Nm-2, ρ = 3500kg/m3, θD = ?
The volume
The mean velocity of sound in the medium is given by
Now making use of Debye frequency equation in terms of mean velocity and also taking into Account the expression hvD = kθD, the Debye temperature can be written as
Substituting different values, we get
Q.7. A copper wire of diameter 1.0 mm and length 2.0 m carries a direct current of 5.0 A. Calculate to the drift velocity of the electrons in the copper, if n = 8.47 x 1028 m-3.
Q.8. Estimate the typical conductivity of a metal at 295 K assuming that the mean free path is about 10Å and that the number of valence electrons is about 1029 m-3.
Here

Q.9. Prove that compressibility of the free electron gas is given by β = 3/2nEF.
For free electron gas; Etotal = Ek = kinetic emergy only = 3/5(EF)
Q.10. Find the number of energy states available for the electrons in a cubical box of 0.01 m side lying below an energy of 4 eV.
The number of energy states below 4eV is
Q.11. If the Fermi energy of the electron is 2.1eV , find the Fermi velocity and the Fermi temperature.
Q.12. Show that the wavelength associated with an electron having energy EF is given by
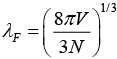 . If this wavelength is 4.6Å, find the Fermi temperature.
. If this wavelength is 4.6Å, find the Fermi temperature.
We have kF = (3π2N/V)1/3
∴ TF = 8.25 x 104 K
Q.13. What is the Fermi energy for the free electron gas in a silver, if the density of conduction electron is 5.8 x 1028m-3. What is the Fermi velocity?
3π2n = 3 x (9.86) 5.8 x 1028 = 156.2 x 1028 = 1562 x 1027 = 11.6 x 109 = 134.56 x 1018
Q.14. Calculate the electronic specific heat of Cu(EF = 7.05 eV) at 600 K.
Ce = 2.995J (kmol )-1 K-1
Q.15. Find the Fermi energy and Fermi velocity of conduction electrons in a Na metal (a = 4.3Å).
Here Na is bcc . Hence n = a3/2
6π2 = 6 x 3.14 x 3.14 = 59.1 ⇒ (6π2)1/ 3 = 3.9 ⇒ (6π2)2/3= 15.2
Now (1/2)mv2F = EF
Q.16. The valence band of a simple cubic metal has the form E = Ak2 + B where A = 10-38 Jm2 Calculate m*/m.
E = Ak2 + B

Q.17. Using the tight binding model, the energy wave vector dispersion relation for one-dimensional crystal of a lattice constant a is E(k) = E0 - α - 2βcos ka.
(a) What is the energy of the top of the band? Bottom of the band? Find the energy gap (Eg).
(b) Find m* near bottom of the band.
(c) Obtain an expression of m* as a function of k.
(d) Find the value of k, at which the velocity of an electron is maximum. What is the maximum velocity (vmax)?
(a) Etop = E0 - α + 2β, ∵ ka = π
Ebottom = E0 - α + 2β, ∵ ka =0
Eg = Etop - Ebottom = 4β
(b) Near the bottom, k → 0 and coska = 1 - (1/2)ka2
∴ E(k → 0) = E0 - α - 2β(1 - (1/2)k2a2)
(c) From equation (i),
(d)
v = vmax sin ka = 1 or ka = nπ/2 ⇒ k = nπ/2a
|
91 videos|21 docs|25 tests
|
FAQs on Einstein & Debye Theory of Specific Heat: Assignment - Solid State Physics, Devices & Electronics
| 1. What is the Einstein theory of specific heat? |  |
| 2. What is the Debye theory of specific heat? |  |
| 3. How do the Einstein and Debye theories of specific heat differ? |  |
| 4. What are the limitations of the Einstein and Debye theories of specific heat? |  |
| 5. How do the Einstein and Debye theories of specific heat contribute to our understanding of solids? |  |
|
91 videos|21 docs|25 tests
|

|
Explore Courses for Physics exam
|

|
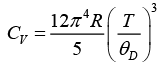
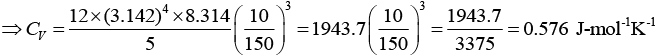
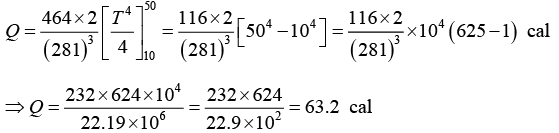
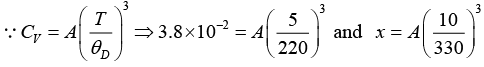
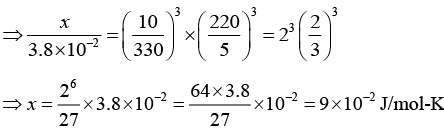
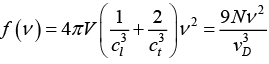
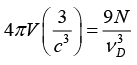
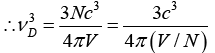
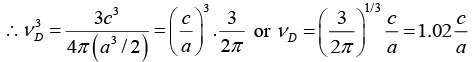
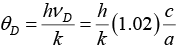 or
or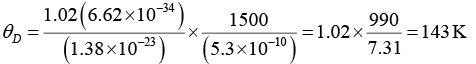
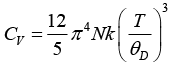
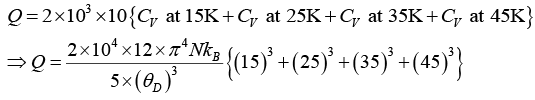
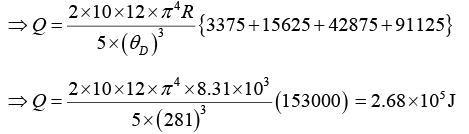
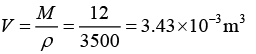
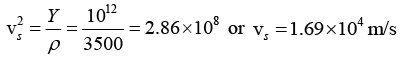
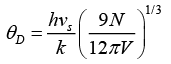
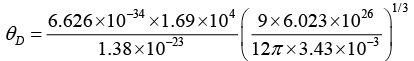
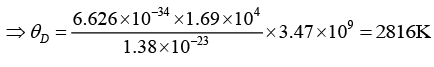
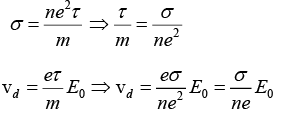
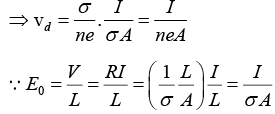
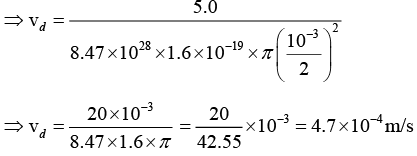
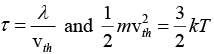
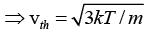
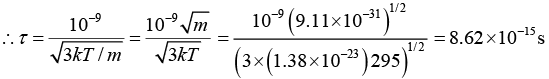
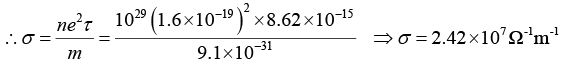
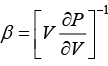
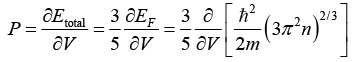
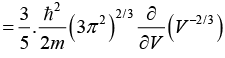
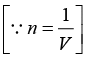
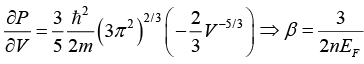
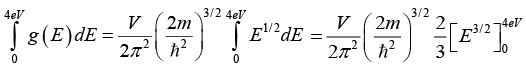
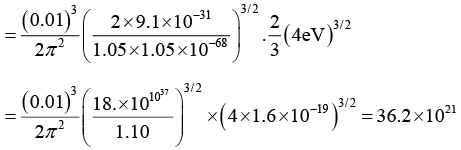
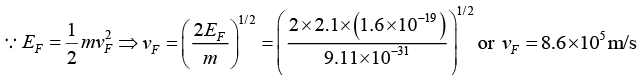
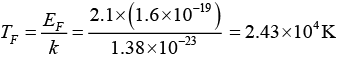
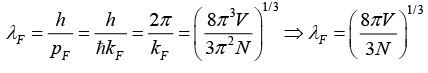
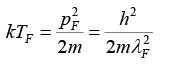
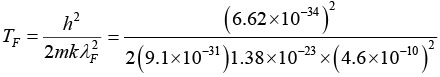
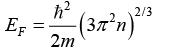
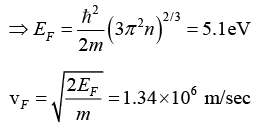
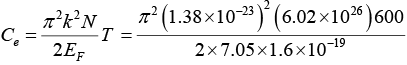
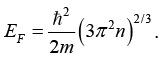 Here Na is bcc . Hence n = a3/2
Here Na is bcc . Hence n = a3/2