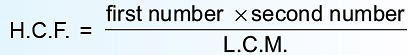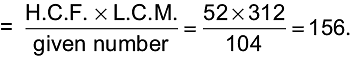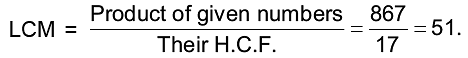HCF and LCM Class 5 Notes Maths
| Table of contents |

|
| Prime Numbers |

|
| Composite Numbers |

|
| Divisibility Rules |

|
| Factors and Multiples |

|
| Highest Common Factor H.C.F |

|
| Lowest Common Multiple L.C.M |

|
| Exponential Notation or Index Notation |

|
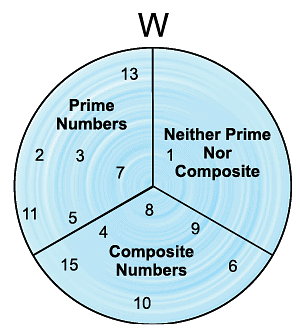
Prime Numbers
The numbers which cannot be broken into factors other than 1 and itself are known as prime numbers, e.g., 2, 3, 5, 7, 11, 13,...
It is important to note that
1 is not a prime number
2 is the only even number which is prime.
Composite Numbers
Numbers that can be expressed as a product of factors other than 1 and itself are known as composite numbers, e.g., 4, 6, 8, 9, 10, 12, 14, 15,...
Note that composite numbers are not only even. The collection of composite numbers is a mixture of even numbers and odd numbers both.
4, 6, 8, 10, ...... are even composite numbers
9, 15, 21, ...... are odd composite numbers.
Since we cannot express 1 as a product of two different factors other than 1 and itself, we say that 1 is the only exceptional number which is neither prime nor composite.
 To determine whether a particular number is prime or composite, we don't have a set formula. For this, we have to perform actual division many times to check whether we can divide the given number by another number or not. A reek mathematician, Eratosthenes developed a method in the 3rd century B.C. to find prime numbers. His method for finding prime numbers is known as the Sieve method. For numbers from 1 to 100, this method is explained below.
To determine whether a particular number is prime or composite, we don't have a set formula. For this, we have to perform actual division many times to check whether we can divide the given number by another number or not. A reek mathematician, Eratosthenes developed a method in the 3rd century B.C. to find prime numbers. His method for finding prime numbers is known as the Sieve method. For numbers from 1 to 100, this method is explained below.
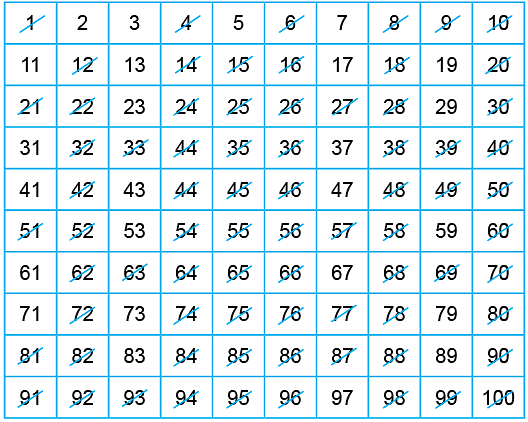
- First, we write all the numbers from 1 to 100.
- Then cross out the first number 1, it is neither prime nor composite.
- The next number is 2, it is the first prime number. We keep it and cross out all the multiples of 2.
- The next number is 3, it is the next prime number. We keep it and cross out all the multiples of 3.
- The next uncrossed number is 5, which is the next prime number. Keep it and cross out all the multiples of 5.
- The next uncrossed number is 7, which is the next prime number. Keep it and cross out all the multiples of 7.
Continue keeping the next prime numbers and crossing out their multiples, until we are left with prime numbers only.
Thus, prime numbers from 1 to 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Twin Primes
Two Prime numbers which differ by 2 are called twin primes, e.g., (3, 5) (5, 7) (11, 13 ) (17, 19)
Such numbers will form a pair of consecutive odd numbers.
Prime Triplet
A set of three prime numbers differing by 2 form a prime triplet, e.g., (3, 5, 7)
(3, 5, 7) is the only prime triplet.
Coprime Numbers
- A pair of two numbers which have no common factor other than 1 are called coprimes, e.g., (2, 3) (3, 4) (4, 5) (3, 7) (4, 9)
- Coprime numbers need not be rime numbers themselves, e.g, (4, 9)
The only condition for two numbers to be coprimes is that there is not even a single number, other than 1, which can divide both of them.
Divisibility Rules
Divisibility rules help us to find whether a number divides another number completely without performing actual division.
- Divisibility by 2
A number is divisible by two if it has 0, 2, 4, 6 and 8 in one place.
For example, 240; 1,752; 2,014; 85,396; and 53,178 are divisible by 2 because their ones digits are 0, 2, 4, 6 and 8 respectively. - Divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example, 4,518 is divisible by 3, because
The sum of its digits = 4 + 5 + 1 + 8 = 18, which is divisible by 3.
Consider 72,019.
The sum of its digits = 7 + 2 + 0 + 1 + 9 = 19, which is not divisible by 3. So 72,019 is not divisible by 3. - Divisibility by 4
A number is divisible by 4 if the number formed by its digits in tens and ones places is divisible by 4
For example, 7,80,456 is divisible by 4, because the number formed by its tens and ones digits is 56, which is divisible by 4.
7,52,963 is not divisible by 4, because the number formed by its tens and one's digits is 63, which is not divisible by 4. - Divisibility by 5
A number is divisible by 5 if it has 0 or 5 in its place
For example, 8,975 is divisible by 5, because it has 5 in its ones place.
Also, 75,293 is not divisible by 5, because its one digit is neither 0 nor 5. - Divisibility by 6
6 is a multiple of 2 and 3.
If we write some multiples of 2, 3 and 6, we have
Multiples of 2 are 2, 4, 8, 10,
8, 10,  14, 16,
14, 16,  20, 22,
20, 22,  26,...
26,...
Multiples of 3 are 3, 9,
9,  15,
15,  21,
21,  27,...
27,...
Multiples of 6 are,

We find that 6, 12, 18, and 24, come in both the lists of the multiples of 2 and 3.
These numbers make the table of 6. So we can say that
If a number is divisible by two coprime numbers, it is divisible by their product also.
Therefore, the numbers that are multiples of 6 are multiples of 2 and 3.
Thus, a number is divisible by 6 if it is divisible by 2 and 3 both. - Divisibility by 8
a number is divisible by 8 if the number formed by its digits in hundreds of tens and one's laces is divisible by 8.
For example, 72,15,976 is divisible by 8, because the number formed by its hundreds, tens and one's digits is 976, which is divisible by 8.7,41,138 is not divisible by 8 because the number formed by its hundreds of tens and one's digits is 138, which is not divisible by 8. - Divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
For example, a number 90,981 is divisible by 9,
because the Sum of its digits = 9 + 0 + 9 + 8 + 1 = 27, which is divisible by 9.
Consider 54,731.
The sum of its digits = 5 + 4 + 7 + 3 + 1 = 20, which is not divisible by 9. So, 54,731 is not divisible by 9. - Divisibility by 10
A number is divisible 10 if it has 0 at its one's place
For example, 98,370 is divisible by 10, because it has 0 in its units place.
53,948 is not divisible by 10, because its one digit is not 0. - Divisibility by 11
A number is divisible by 11 if the difference between the sum of its digits in odd laces and the sum of its digits in even laces (starting from the unit's lace) is either 0 or divisible by 11.
Consider the following numbers.
4,961, 61,831, 96,251
In 4,961, the sum of the digits in odd places is 10(1 + 9 = 10) and the sum of digits in even places is 10 (6 + 4 = 10)
Difference of the two sums = 10 – 10 = 0.
Hence, 4,981 is divisible by 11.
In 61,831, the sum of the digits in odd places is 15 (1 + 8 + 6 = 15) and the sum of the digits in even places is 4(3 + 1 = 4).
The difference between the two sums = is 15 – 4 = 11, which is divisible by 11. Hence, 61,831 is divisible by 11.
In 96,251, the sum of the digits in odd places is 12 (1 + 2 + 9 = 12) and the sum of the digits in even places is 11 (5 + 6 = 11).
The difference between the two sums = 12 – 11 = 1, which is not divisible by 11. Hence, 96,251 is not divisible by 11.
 Divisibility Rules
Divisibility Rules
Factors and Multiples
When a number divides another number exactly i.e. without leaving any remainder, the divisor is called a factor of the dividend.
The dividend is called a multiple of the divisor.
For example, 42 is divisible by 7, so 7 is a factor of 42 and 42 is a multiple of 7.
Consider, 105 = 7 × 15.
Here also, 7 and 15 are factors of 105 and 105 is a multiple of both 7 and 15.
- Even Numbers: Numbers divisible by 2 are called even numbers.
For example, 2, 4, 6, 8, ........ are even numbers. - Odd Numbers: Numbers not divisible b 2 are called odd numbers
For example, 1, 3, 5, 7, 9, ........ are odd numbers.
Common Factors
Observe the following:
(a) All the factors of 15 are 1, 3, 5 and 15.
All the factors of 20 are 1, 2, 4, 5, 10 and 20.
Thus, common factors of 15 and 20 are 1 and 5.
(b) All the factors of 32 are 1, 2, 4, 8, 16, 32.
All the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
Thus, common factors of 32 and 48 are 1, 2, 4, 8, 16.
Edurev Tips: does not have to factors So, it is not a prime number. Also, does not have more than to factors. So, it is not a composite number. Hence, is neither a prime nor a composite number
Highest Common Factor H.C.F
In the example given above, the common factors of 15 and 20 are 1 and 5. Out of these two common factors, 5 is the highest and greatest common factor. Therefore, we call 5 the highest common factor of 15 and 20.
Again in example by, common factors of 32 and 48 are 1, 2, 4, 8 and 16. Out of these, 16 is the highest and greatest common factor. Therefore, 16 is the highest common factor of 32 and 48.
Hence, the H.C.F. highest common factor of two or more than two numbers is the highest greatest among all their common factors.
The highest common factor H.C.F. is also called the Greatest common divisor (G.C.D.).
Example 1: Find all the common factors of:
(a) 24 and 40
(b) 20 and 64
(a) 24 = 1 × 24, 24 = 2 × 12,
24 = 3 × 8, 24 = 4 × 6
Therefore, all the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
Also, 40 = 1 × 40, 40 = 2 × 20, 40 = 4 × 10, 40 = 5 × 8.
Therefore, all the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
Thus, common factors of 24 and 40 are 1, 2, 4 and 8.
(b) 20 = 1 × 20, 20 = 2 × 10, 20 = 4 × 5
Therefore, all the factors of 20 are 1, 2, 4, 5, 10 and 20.
Also, 64 = 1 × 64, 64 = 2 × 32, 64 = 4 × 16, 64 = 8 × 8.
Therefore, all the factors of 64 are 1, 2, 4, 8, 16, 32 and 64.
Thus, common factors of 20 and 64 are 1, 2 and 4.
Example 2: Find the H.C.F. of 18, 45 and 63.
18 = 1 × 18, 18 = 2 × 9, 18 = 3 × 6
All the factors of 18 are 1, 2, 3, 6, 9 and 18.
Also, 45 = 1 × 45, 45 = 3 × 15, 45 = 5 × 9.
All the factors of 45 are 1, 3, 5, 9, 15 and 45.
Also, 63 = 1 × 63, 63 = 3 × 21, 63 = 7 × 9.
All the factors of 63 are 1, 3, 7, 9, 21 and 63.
Common factors of 18, 45 and 63 are 1, 3 and 9.
Thus, H.C.F. of 18, 45 and 63 is 9.
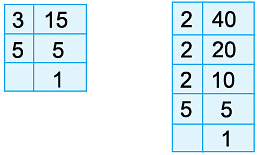
Example 3: Find the H.C.F. of 15 and 28.
15 = 1 × 15, 15 = 3 × 5.
All the factors of 15 are 1, 3, 5 and 15.
Also, 28 = 28 × 1, 28 = 2 × 14, 28 = 4 × 7
All the factors of 28 are 1, 2, 4, 7, 14 and 28.
Common factor of 15 and 28 is 1.
Thus, H.C.F. of 15 and 28 is 1.
We call 15 and 28 are co-prime.
Edurev Tips: Two numbers are said to be co-prime, if their H.C.F. is 1
Properties of H.C.F
- The H.C.F. of two or more numbers cannot be greater than one of them.
- If a number is a factor of another number, then their H.C.F. is the smaller number.
Common Multiples
Let us try to find out the multiples of 8 and 12.
Multiples of 8 are 8, 16, 24, 32, 40, 48, .....................
Multiples of 12 are 12, 24, 36, 48, 60, 72, .....................
Thus, common multiples of 8 and 12 are 24, 48, .....................
Again, find the common multiples of 10 and 15.
Multiples of 10 are 10, 20, 30, 40, 50, 60, .....................
Multiples of 15 are 15, 30, 45, 60, 75, .....................
Thus, common multiples of 10 and 15 are 30, 60, .....................
Lowest Common Multiple L.C.M
In the examples given above, common multiples of 8 and 12 are 24, 48, .... and common multiples of 10 and 15 are 30, 60,...
The lowest common multiple of 8 and 12 is 24.
And the lowest common multiple of 10 and 15 is 30.
Hence, the lowest common multiple L.C.M. of two or more numbers is the smallest of their common multiples.
Example 4: Find the first two common multiples of:
(a) 4 and 10
(b) 5, 6 and 15.
(a) Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, .....
Multiples of 10 are 10, 20, 30, 40, .....
Thus, the first two common multiples of 4 and 10 are 20 and 40.
(b) Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 60, 65, .....
Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, .....
Multiples of 15 are 15, 30, 45, 60, 75, .....
Thus, the first two common multiples of 5, 6 and 15 are 30 and 60.
Example 5: Find the L.C.M. of 12 and 18.
Multiples of 12 are 12, 24, 36, 48, 60, 72, .....
Multiples of 18 are 18, 36, 54, 72, 90, .....
Thus, common multiples of 12 and 18 are 36, 72, .....
Therefore, L.C.M. of 12 and 18 is 36.
Properties of L.C.M
- The L.C.M. of two co-prime numbers is their product.
- If one number is the multiple of the other, then their L.C.M. is the greater number.
- The L.C.M. of two or more numbers cannot be less than one of them.
Exponential Notation or Index Notation
When a number is multiplied with itself several times, we express the product in the form given below; called the exponential or index notation.
In 32, 3 is called the base and 2 is called the exponent or index or power.
Similarly, in 64, 6 is the base and 4 is the exponent index.
Observe the following examples:
2 × 2 × 2 × 3 × 3 = 23 × 32
5 × 5 × 5 × 5 × 8 × 8 × 8 = 54 × 83
10 × 10 × 10 × 10 × 10 × 17 × 17 × 17 × 17 = 105 × 174
Example 6: Write in the exponential form:
(a) 5 × 5 × 5 × 5 × 5 × 5
(b) 8 × 8 × 8 × 8 × 9 × 9
(a) 5 × 5 × 5 × 5 × 5 × 5 = 56
(b) 8 × 8 × 8 × 8 × 9 × 9 = 84 × 92.
Example 7: Write in the product form:
(a) 87
(b) 63 × 114
(a) 87 = 8 × 8 × 8 × 8 × 8 × 8 × 8
(b) 63 × 114 = 6 × 6 × 6 × 11 × 11 × 11 × 11.
Edurev Tips: In index notation, we cannot interchange base and exponent, i.e., 23 is not equal to 32.
Prime Factorisation
Observe the following:
54 = 1 × 54, 54 = 2 × 27, 54 = 3 × 18, 54 = 6 × 9, 54 = 2 × 3 × 9,
54 = 2 × 3 × 3 × 3
We see that in 54 = 2 × 3 × 3 × 3, all the factors are prime.
Thus, the prime factorisation of 54 is 2 × 3 × 3 × 3.
Similarly, the prime factorisation of 24 is 2 × 2 × 2 × 3.
The prime factorisation of 45 is 3 × 3 × 5.
When a number is expressed as a product of prime numbers, we call it prime factorization
To get the prime factorisation of a number, we divide the given number by the prime numbers 2, 3, 5, 7, 11, etc., so long as the quotient is divisible by that number.
Factor Tree
The prime factorisation of a number can be shown diagrammatically, known as a factor tree.
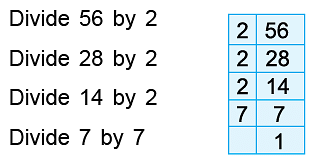
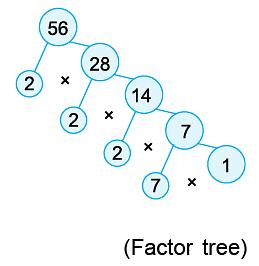
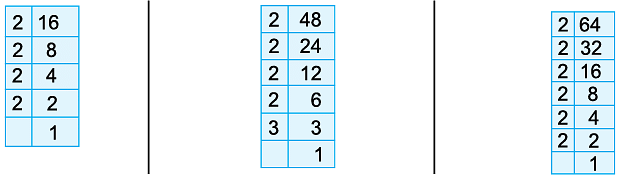
Example 8: Express 56 as the product of prime factors.
We proceed as follows:
Hence, the prime factorisation of 56 is
= 2 × 2 × 2 × 7 = 23 × 7.
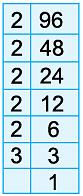
Example 9: Draw a factor tree to find the prime factorisation of 96.
Thus, the prime factorisation of 96 is
= 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3.
H.C.F by Prime Factorisation Method
To find the H.C.F. of two or more numbers, we express each one of them as the product of prime factors. Then, the product of terms containing the least powers of common factors is their H.C.F.
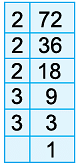
Example 10: Find the H.C.F. of 28 and 72 by the prime factorisation method.
Resolving each of the given numbers into prime factors, we get
28 = 2 × 2 × 7 = 22 × 7
72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
H.C.F. of 28 and 72 = Product of common prime factors
= Product of terms with smallest powers of common factors
= 22 = 4
Thus, H.C.F. of 28 and 72 = 4.
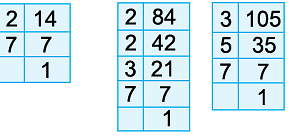
Example 11: Find the H.C.F. of 14, 84 and 105.
Resolving the given numbers into prime factors, we get.
14 = 2 × 7
84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
105 = 3 × 5 × 7
H.C.F. of 14, 84 and 105 = Product of common prime factors
= Product of terms with smallest powers of common factors.
= 71 = 7
Thus, the H.C.F. of 14, 84 and 105 = 7.
H.C.F by Long Division Method
To find the HCF of two or three given numbers, divide the greater number by the smaller one. Then, divide the divisor by the remainder. Go on repeating the process of dividing the preceding divisor by the remainder, till zero remainder is obtained. The last divisor is the HCF of the given numbers.
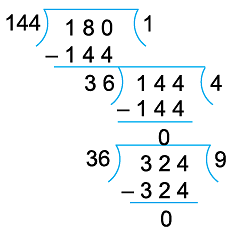
Example 12: Find the H.C.F. of 144, 180 and 324.
We first find the HCF of any two numbers (144 and 180).
Since, last divisor is 36, so 36 is the HCF of 144 and 180.
Now, we find the HCF of 36 and 324.
Hence, HCF of 144, 180 and 324 is 36.
L.C.M by Prime Factorisation Method
To find the L.C.M. of two or more numbers, we express each one of them as the product of prime factors. Then, the product of terms with the highest powers of all the factors gives their L.C.M.
Example 13: Find the L.C.M. of 15 and 40, using the prime factorisation method.
Resolving the given numbers into prime factors, we get
So, 15 = 3 × 5
Also, 40 = 2 × 2 × 2 × 5 = 23 × 5.
The different prime factors of 15 and 40 are 2, 3 and 5.
L.C.M. of 15 and 40 = Product of terms containing highest powers of 2, 3 and 5
= 23 × 3 × 5 = 8 × 3 × 5 = 120.
Example 14: Find the L.C.M. of 16, 48 and 64.
Resolving each of the given numbers into prime factors, we get
16 = 2 × 2 × 2 × 2 48 = 2 × 2 × 2 × 2 × 3, 64 = 2 × 2 × 2 × 2 × 2 × 2
= 24 = 24 × 3 = 26
The different prime factors of 16, 48 and 64 are 2 and 3.
Thus, L.C.M. of 16, 48 and 64
= Product of terms containing highest powers of 2 and 3.
= 26 × 3
= 64 × 3 = 192.
L.C.M. by Long Division Method
We proceed as below:
- Arrange the given numbers in a line, in an order.
- Divide by a number that exactly divides at least two of the given numbers and carry forward the numbers that are not divisible.
- Repeat the process till none of the two given numbers are divisible by the same number.
- The product of all the divisors and the numbers left undivided is the required LCM.
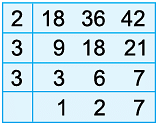
Example 15: Find the LCM of 18, 36, and 42 by long division method.
So, LCM of 18, 36 and 42
= 2 × 3 × 3 × 2 × 7 = 252
Hence, LCM of 18, 36 and 42 = 252.
Relationship Between H.C.F. and L.C.M, of Two Given Numbers
For two given numbers, we have.
- Product of two numbers = Product of their H.C.F. and L.C.M.
(First number × Second number = H.C.F. × L.C.M) 

Example 16: The H.C.F. of two numbers is 52 and their L.C.M is 312. If one of the numbers is 104, find the other.
It is given here that:
H.C.F. = 52, L.C.M. = 312 and one number = 104
The other number
Hence, the other number is 156.
Example 17: The product of two numbers is 867 and their HCF is 17. Find their L.C.M.
We know that:
Hence, the LCM of given numbers is 51.
|
32 videos|57 docs|45 tests
|
FAQs on HCF and LCM Class 5 Notes Maths
| 1. What are prime numbers and how do they differ from composite numbers? |  |
| 2. What are the divisibility rules for numbers? |  |
| 3. How do you find the Highest Common Factor (HCF) of two numbers? |  |
| 4. What is the difference between Highest Common Factor (HCF) and Lowest Common Multiple (LCM)? |  |
| 5. What is exponential notation and how is it used in mathematics? |  |

|
Explore Courses for Class 5 exam
|

|
 8, 10,
8, 10,  14, 16,
14, 16,  20, 22,
20, 22,  26,...
26,... 9,
9,  15,
15,  21,
21,  27,...
27,...