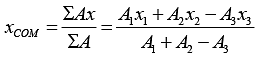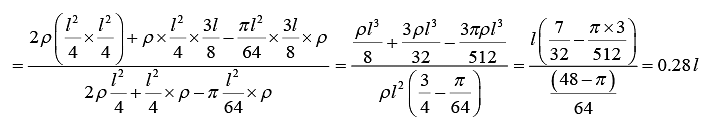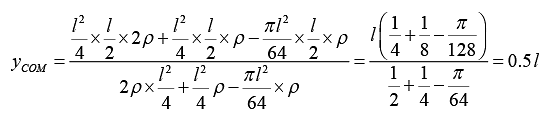Centre of Mass | Mechanics & General Properties of Matter - Physics PDF Download
Centre of Mass
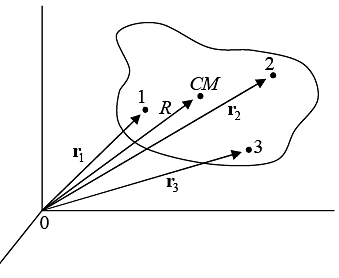
Consider a system composed of N particles with each particle's mass described by mi, where i is an index from i = 1 to i = N . The total mass of the system is denoted by M,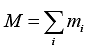
where the summation over i runs from i = 1 to i = N.
Such a system is displayed in figure given. If the vector connecting the origin with the ith particle is ri then the vector defining the position of the system's center of mass is 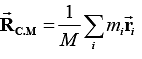
 The position of the centre of mass is defined by RCM ≡
The position of the centre of mass is defined by RCM ≡ 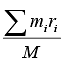
For N number of mass elements, if rj is the position of the jth element, and mj is its mass, then the center of mass is defined as 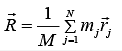
Example 1: The position vector of three particles of mass m1 = 1kg, m2 = 2 kg and m3 = 3kg are 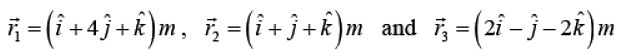
respectively. Find the position vector of their centre of mass.
The position vector of COM of the three particles will be given by
Substituting the values, we get
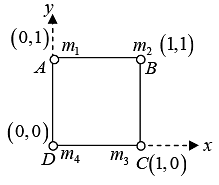
Example 2: Four particles of mass 1 kg, 2kg, 3kg and 4kg are placed at the four vertices A,B, C and D of a square of side 1 m. Find the position of centre of mass of the particles.
Assuming D as the origin, DC as x - axis and DA as y - axis, we have
m1 = 1kg, x1, y1) = ( 0,1 m)
m2 = 2kg, x2, y2) = (1m,1m)
m3 = 3kg, x3, y3) = (1 m, 0)
m4 = 4kg, x4, y4) = (0, 0)
and co-ordinates of their COM are
Similarly,
∴ (xCOMyCOM = (0.5,0.3)
Rigid Body Dynamics
A rigid body is defined as system of particles in which the distance between any two particles remains fixed throughout the motion.
Degree of Freedom of Rigid Body
To define rigid body, there must be minimum 3 non-collinear points.
Let P1 (x1, y1, z1), P2 (x2, y2 , z2) , P3 (x3, y3, z3) are three non-collinear points.
So, equation of constrained is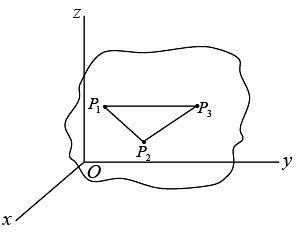 r12 = (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2 = c1
r12 = (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2 = c1
r23 = (x2 - x3)2 + (y2 - y3)2 + (z2 - z3)2 = c2
r13 = (x1 - x3)2 + (y1 - y3)2 + (z1 - z3)2 = c3
Dof = 3N - K
3 x 3 - 3 = 6
So there is six degree of freedom for rigid body
Center of Mass of Continuous System
The result is not rigorous, since the mass elements are not true particles. However, in the limit where N approaches infinity, the size of each element approaches zero and the approximation becomes exact. This limiting process defines an integral.
This limiting process defines an integral.
Formally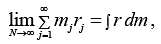 where dm is a differential mass element. Then,
where dm is a differential mass element. Then,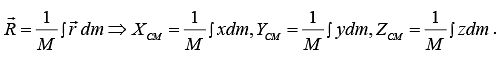
To visualize this integral, think of dm as the mass in an element of volume dV located at position r. If the mass density at the element is ρ, then dm = ρdV and 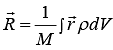 . This
. This
integral is called a volume integral.
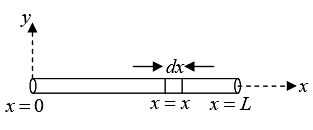
Example 3: A rod of length L is placed along the x - axis between x = 0 and x = L. The linear density (mass/length) λ of the rod varies with the distance x from the origin as λ = Rx . Here, R is a positive constant. Find the position of centre of mass of this rod.
Mass of element dx situated at x = x is
dm = λdx = Rx dx
The COM of the element has coordinates (x,0,0).
Therefore, x -coordinate of COM of the rod will be
The y -coordinate of COM of the rod is yCOM(as y = 0 )
Similarly, zCOM = 0 Hence, the centre of mass of the rod lies at
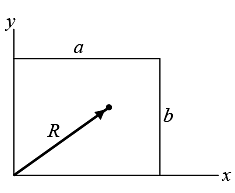
Example 4: Find the center of mass of a thin rectangular plate with sides of length α and b, whose mass per unit area σ varies in the following fashion:
σ = σ0(xy/αb) where σ0 is a constant.
We find M , the mass of the plate, as follows:
We first integrate over x , treating y as a constant.
The x component of R is
Similarly,
⇒ y = 2/3 b So center of mass is
Example 5 : Find the centre of mass of semicircular disc of mass M and radius R.
From the circular symmetry x = r cos θ, y = r sin θ
Example 6: Find the centre of mass of a hollow hemisphere of radius R and mass M.
Consider a ring at angle θ from the base area of ring This problem can be solved in spherical symmetry
x = R sinθ cos∅ , y = R sinθ sin∅ , z = R cos θ
XC.M = ∫xdmR sin θ cos ∅.sin θdθd∅
Second method
The integral is over three dimensions, but the symmetry of the situations lets us treat it as a one dimensional integral. We mentally subdivide the hemisphere into a pile of thin disks. Consider the circular disk of radius r and thickness dz . Its volume is dV = πr2dz , and its mass is
dM = ρdV= (M/V) dV, where V = 2/3 πR3.
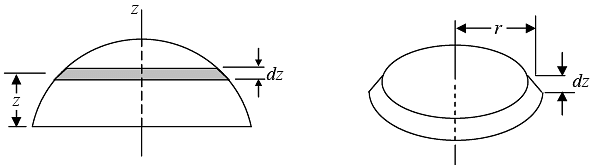
Hence, 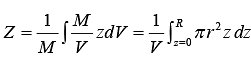
To evaluate the integral, we need to find r in terms of z. Since, r2 = R2 - z2, we have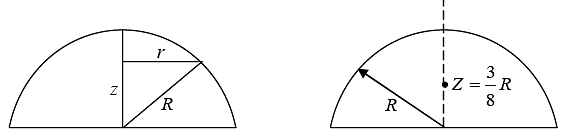

Example 7: Find the centre of mass triangular plate of Mass M . Where l and h are given parameter shown in figure.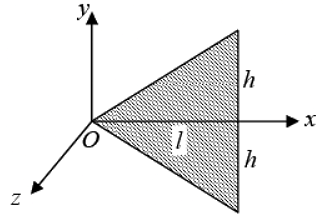
lf some mass M1 is removed from a rigid body of mass M , then the position of centre of mass of the remaining portion is obtained from the following formulae:Here,
the values mass and center of mass of the whole mass while are
the values for the mass which has been removed.
Example 8: Find the position of centre of mass of the remaining plate when a circle is cut from right half radius of circle is l/8. Centre of circle is in centre of the right part of the plate.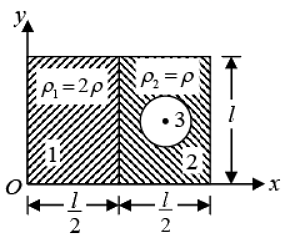
Area

A1 l2/4 l/4 l/2
A2 l2/4 3l/8 l/2
A3 πl2/64 3l/8 l/2
Taking origin at corner O
Centre of mass is (0.28l, 0.5l).
|
61 videos|23 docs|25 tests
|
FAQs on Centre of Mass - Mechanics & General Properties of Matter - Physics
| 1. What is the definition of the center of mass? |  |
| 2. How is the center of mass calculated for a rigid body? |  |
| 3. Why is the center of mass important in rigid body dynamics? |  |
| 4. Can the center of mass be outside the physical boundaries of an object? |  |
| 5. How does the center of mass affect the stability of a rigid body? |  |
|
61 videos|23 docs|25 tests
|

|
Explore Courses for Physics exam
|

|
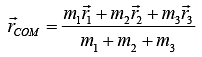
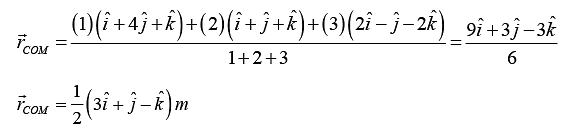
 m1 = 1kg, x1, y1) = ( 0,1 m)
m1 = 1kg, x1, y1) = ( 0,1 m)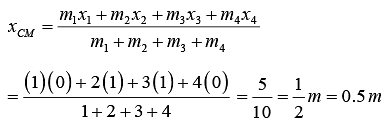
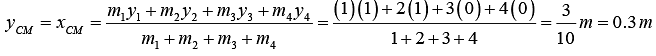
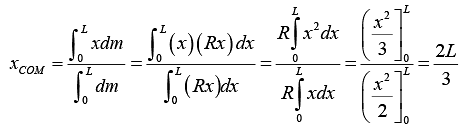
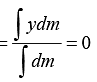 (as y = 0 )
(as y = 0 )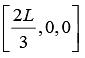
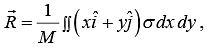
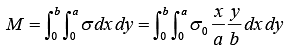
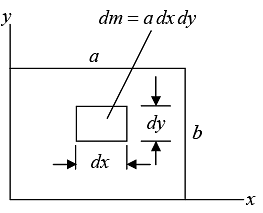 We first integrate over x , treating y as a constant.
We first integrate over x , treating y as a constant.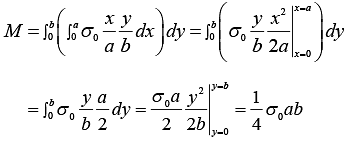
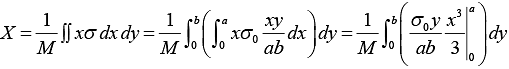
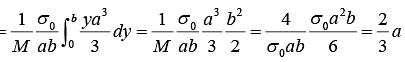

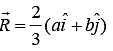
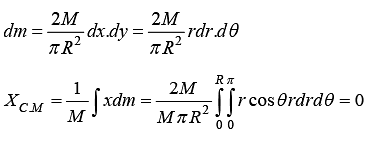
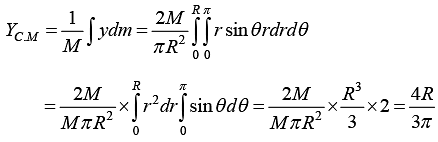

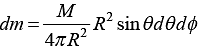
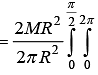 R sin θ cos ∅.sin θdθd∅
R sin θ cos ∅.sin θdθd∅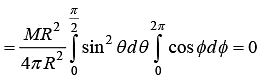
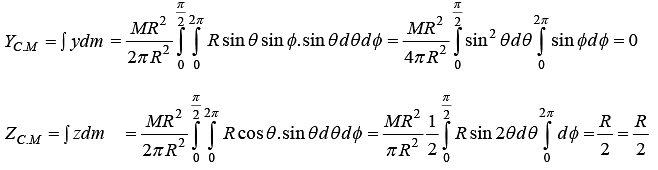
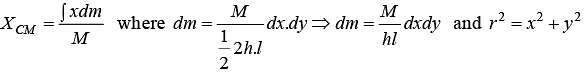

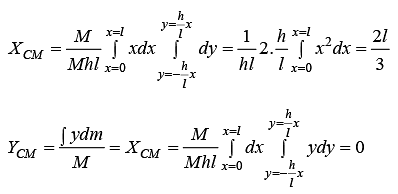
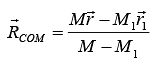
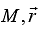 the values mass and center of mass of the whole mass while are
the values mass and center of mass of the whole mass while are the values for the mass which has been removed.
the values for the mass which has been removed.