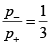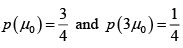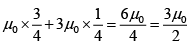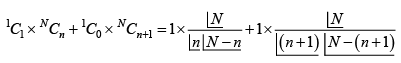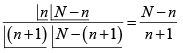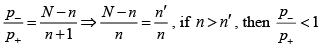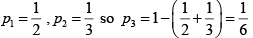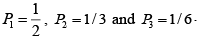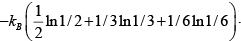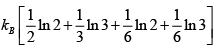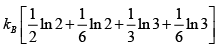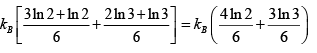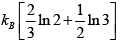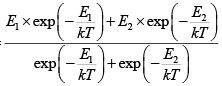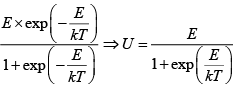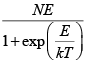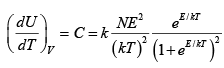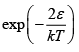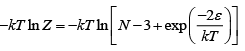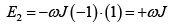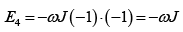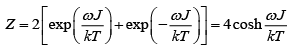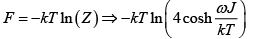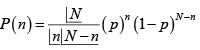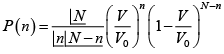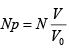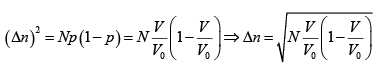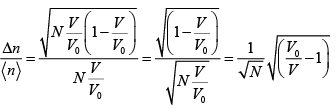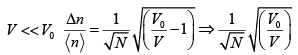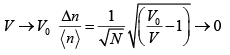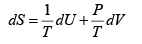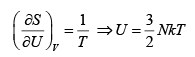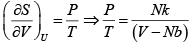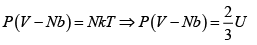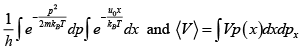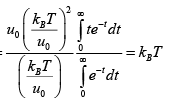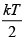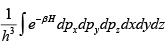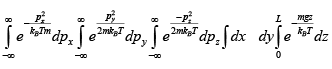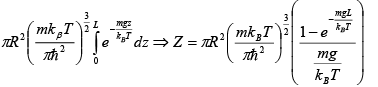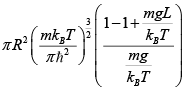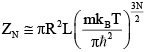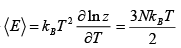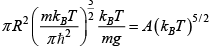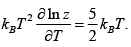Statistical Mechanics: Assignment | Kinetic Theory & Thermodynamics - Physics PDF Download
Q.1. One spin in the thermal contact with a small spin system
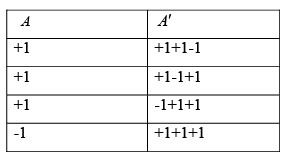
Consider a system A consisting of a spin having1/2 particle with magnetic moment μ0 ,and another system A' consisting of 3 spins 1/2 particle, each having magnetic moments μ0 . Both systems are located in the same magnetic field B . The systems are placed in contact with each other, in such a way, they are free to exchange energy. Suppose that, when the moments of A , points up (i.e., when A is in its + state), two of the moments of A' points up and one of them points down.
(a) Count the total number of state accessible to the combined system A+ A' , when the moment of A , points up, and points down respectively. Hence, calculate the ratio P- / P+ , where P- is the probability that the moment of A points down and P+ is the probability that it points up. Assume that the total system A+ A' is isolated.
(b) Find the average of magnetic moment of sub system A'.
If A has up state and A' has situation that 2 spin is in up state and 1 is in down state and has total energy of the system ( A +A') as 2μ0B , then the total number of microstate is given by
= 3 + 1 = 4 number of microstate .
For sub system A p+ = 3/4 and p- = 1/4
(a) For subsystem A' ,
Thus (M) =
Solution 3: Total number of microstate
If moment of A points up, then A' has
number of microstate
(b) If moment of A points down, then A' has n + 1 up and N - (n - 1) spin points down,
so number of microstate is
(c)
=
For n >> 1 and n' >> 1 , the ratio P- /P+ larger or smaller then unity if n >n'
Q.2. In a thermodynamic system in equilibrium, each molecule can exist in three possible states with two of them has probabilities 1/ 2, 1/ 3 respectively. Find entropy per molecule.
S =
S =
S =
S =
=
S =
Q.3. Consider a system of N particles obeying classical statistics, each of which can have an energy 0 or E . The system is in thermal contact with a reservoir maintained at a temperature T . Let k denote the Boltzmann constant. Find heat capacity C of the system .
U =
E1 = 0, E2 = E for one particle U =
So for N Particle U =
Q.4. Two classical particles are distributed among N (>2) sites on a ring. Each site can accommodate only one particle. If two particles occupy two nearest neighbour sites, then the energy of the system is increased by ∈.
(a) Find partition function
(b) Find The average Helmholtz free energy of the system at temperature T is
Since two particle two nearest neighbour sites, which energy of system increased by ∈, and remining ( N - 3) particle hs zero energy, then particle function is given
z = 2e-β∈ + ( N - 3) e-β .0 = ( N - 3) + 2e-β∈(a) Z = N - 3 +
(b) F =
Q.5. Consider a system of two Ising spins S1 and S2 taking values ± 1with interaction energy given by ε = JεS1S2 . When the system is in thermal equilibrium at temperature T ,
(a) Find partition function of system
(b) Find Helmholtz free energy
(c) Internal energy
The interaction energy is given by E = JεS1S2 where S1 and S2 taking values ± 1 .
Possible values of the Energy of the system are
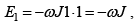
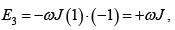
(a)
(b)
(c)
Q.6. Consider an ideal gas of N molecules which is in equilibrium, within a container of volume V0 . Denoted by n is the number of molecules located within any subvolume V of this container. The probability p that a given molecule is located within this subvolume V is then given by p =V /V0 .
(a) Find the probability that out of N molecules, n the number of molecules located
within any subvolume V
(b) What is mean number (n) of molecules within V ? Express your answer in terms of N,V0 and V
(c) Find the standard derivation Δn, where n is the number of molecules located within volume V .
(d) Calculate 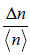 , expressing your answer in terms of N,V0 and V.
, expressing your answer in terms of N,V0 and V.
(e) What is the value of 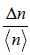 , when 0 V <<V0 ?
, when 0 V <<V0 ?
(f) What value should the standard deviation Δn assume when V →V0 ?
(a)
where
so
(b) (n) =
(c)
(d)
(e)
(f)
Q.7. The quantum states available to a given physical system is are group in gi equally likely states with common energy εi .If pi is probability associated with energy εi such that 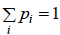 then prove that entropy is given by S=
then prove that entropy is given by S= 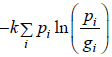
pi =
where Z is partition function
Q.8. A rigid and thermally isolated tank is divided into two compartments of equal volumeV, separated by a thin membrane. One compartment contains one mole of an ideal gas A and the other compartment contains one mole of a different ideal gas B . The two gases are in thermal equilibrium at a temperature T . If the membrane ruptures, the two gases mix. Assume that the gases are chemically inert. The Find the change in the total entropy of the gases on mixing is
For A , number of microstate after mixing is 2
For A , number of microstate before mixing is
⇒ ΔS A = R ln 2 - R ln1 = R ln 2
Similarly, for B ΔSB = Rln 2 ⇒ ΔS =ΔSA + ΔSB = 2 ln 2
The number of microstates of a gas of N particles in a volume V and of internal energy U , is given by
(where a and b are positive constants). Its pressure P , volume V and temperature U , are related by
Then prove that
S =
Q.9. A particle is confined to the region x ≥ 0 by a potential which increases linearly as V(x) = u0x . The find ratio between average potential energy V to average kinetic energy T
Partition function Z =
=
=
=
=
Hence the system is one dimensional so
= 2
Q.10. Gas molecules of mass m are confined in a cylinder of radius R and height L
(with R >> L ) kept vertically in the Earth’s gravitational field.
(a) Find The average energy of the gas at high temperatures (such that mgl<<kBT ) .
(b) Find The average energy of the gas at low temperatures (such that mgl>>kBT )
Z =
Z =
Z =
For high temperature Z =
Z =
⇒
mgl<<kBT ⇒
For low temperature
⇒ Z =
=
⇒ (E) =
|
6 videos|20 docs|32 tests
|
FAQs on Statistical Mechanics: Assignment - Kinetic Theory & Thermodynamics - Physics
| 1. What is the concept of statistical mechanics? |  |
| 2. How is statistical mechanics related to thermodynamics? |  |
| 3. What are the fundamental principles of statistical mechanics? |  |
| 4. How does statistical mechanics explain equilibrium and non-equilibrium systems? |  |
| 5. What are some applications of statistical mechanics? |  |