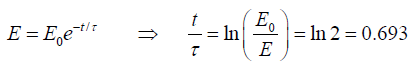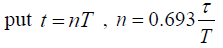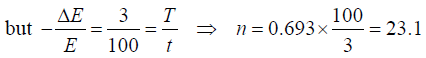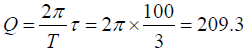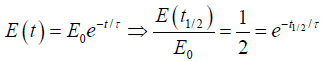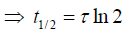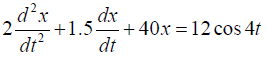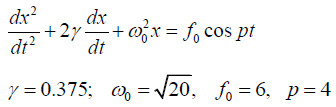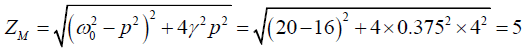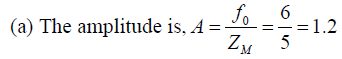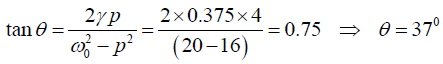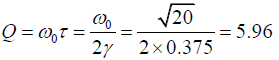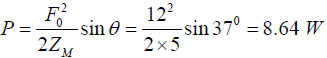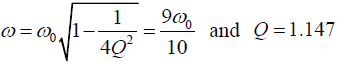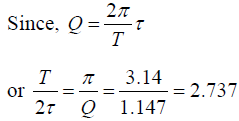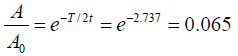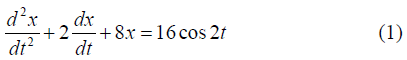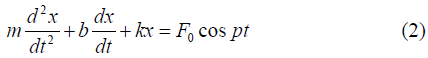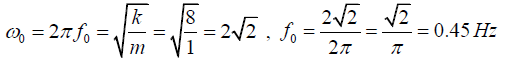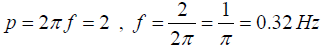Damped Harmonic Oscillations & Forced Oscillations: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. A mass of 4 kg attached to the lower end of a vertical spring of constant 20 N /m oscillates with a period of 10s. Find
(a) The natural time period;
(b) The damping constant and frictional force constant;
(c) The logarithmic decrement
(a)
(b)
Damping constant is
Frictional force constant is b = 2mγ= 2x4x2.146 =17.17 Ns /m
(c) Logarithmic Decrement is λ= γT' = 2.146x10 = 21.46
Q.2. A periodic force acts on a 6 kg mass suspended from the lower end of a vertical spring of constant 150 N/m. The damping force is proportional to the instantaneous speed of the mass and is 80 N when v = 2m/s. Find the resonance frequency.
Damping force Ff = -b.v
or
Q.3. An oscillator has a time period of 3s. Its amplitude decreases by 5% each cycle.
(a) By how much does its energy decrease in each cycle?
(b) Find the time constant
(c) Find the Q factor
(a) Energy is proportional to the square of amplitude
E = constant.A2
(b)
(c)
Q.4. The equation of motion for a damped oscillator is given by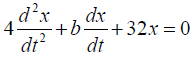
For what range of values for the damping constant will the motion be
(a) Underdamped
(b) Overdamped
(c) Critically damped?
The equation for damped oscillations is
Dividing the equation by 4 ;
Comparing the equation with the standard equation
We get,
The quantityrepresents the damping constant or decay rate of oscillation where
b is the frictional constant.
(a) The motion will be underdamped if
(b) The motion is overdamped if b>16√2
(c) The motion is critically damped if b=16√2
Q.5. The amplitude of a swing drops by a factor 1/ e in 8 periods when no energy is pumped into the swing. Find the Q factor.
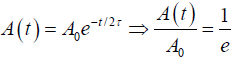
If t = 2τ =8T, τ = 4T,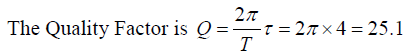
Q.6. An electric bell has a frequency 100 Hz. If its time constant is 2s, determine the Q factor for the bell.
Q =ω0τ = 2πf0τ = 2π x 2 x 100 =1256
Q.7. A 1kg weight attached to a vertical spring stretches it 0.2m . The weight is then pulled
down 1.5 m and released, the frictional force numerically equal to 14 times the
instantaneous speed is acting.
(a) Is the motion underdamped, overdamped or critically damped?
(b) Find the position of the weight at any time.
Equation of motion is
Substituting m = 1.0 kg, b = 14Nm-1s, k = 49Nm-1,(1) becomes(a) Therefore, the motion is critically damped.
(b) For critically damped motion, the equation is x = x0e-γt(1+γt) with γ = 7 and x0 = 1.5, x = 1.5e-7t (1+7t)
Q.8. A lead weight attached to a light extends it by 9.8cm . It is then slightly pulled down and released. Assuming that the logarithmic decrement is equal to 3.1, find the period of the oscillation.
Force = mg = kx
Substituting λ=3.1 and ω0 = 10 in (1), γ = 4.428
Q.9. A damped oscillator loses 3% of its energy in each cycle.
(a) How many cycles elapse before half its original energy is dissipated?
(b) What is the Q factor?
(a)
(b)
Q.10. Show that the time t1/2 for the energy to decrease to half its initial value is related to the time constant by t1/2= τ ln2.
Q.11. The equation of motion for forced oscillations is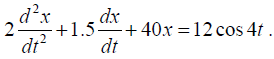
Find
(a) Amplitude
(b) Phase lag
(c) Q factor
(d) Power dissipation
Equation of motion is
Comparing this with the standard equation
Let
(b) The phase lag is,
(c) The quality factor is,
(d) F0 = f0 m = 6x2 =12
The power dissipation is,
Q.12. A damped oscillator has frequency which is 9/10 of its natural frequency. By what factor is its amplitude decreased in each cycle?
Q.13. The position of a particle moving along x - axis is determined by the equation
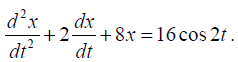
(a) What is the natural frequency of the vibrator?
(b) What is the frequency of the driving force?
This is the equation for the forced oscillations, the standard equation being
Comparing (1) and (2) we find
m=1kg, b=2, k=8, F0=16N, p=2rad/s
(a) the natural frequency of the vibration is
(b) the frequency of the driving force
|
54 videos|22 docs|14 tests
|
FAQs on Damped Harmonic Oscillations & Forced Oscillations: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is a damped harmonic oscillator? |  |
| 2. How does a damped harmonic oscillator differ from an undamped one? |  |
| 3. What are forced oscillations in the context of harmonic oscillations? |  |
| 4. How does resonance occur in forced oscillations? |  |
| 5. What are some real-life examples of damped and forced oscillations? |  |

|
Explore Courses for Physics exam
|

|
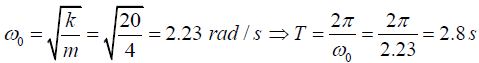
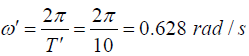
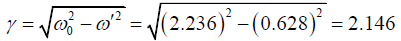
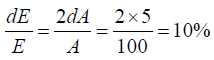
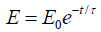
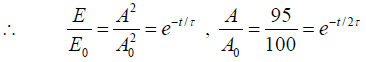
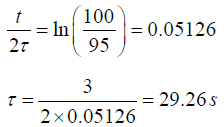
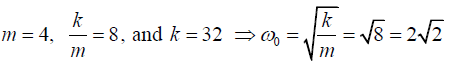
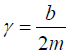 represents the damping constant or decay rate of oscillation where
represents the damping constant or decay rate of oscillation where