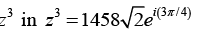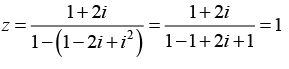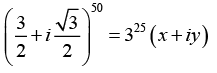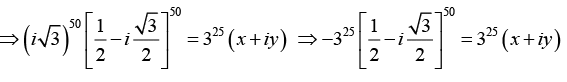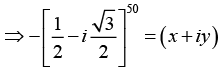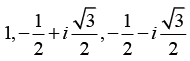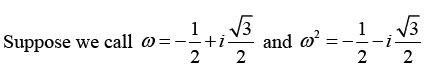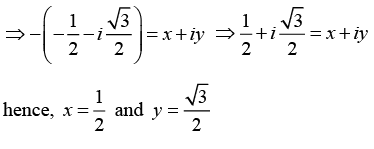Complex Numbers: Assignment | Mathematical Methods - Physics PDF Download
Q.1. Write the complex number 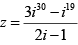 in the form x + iy.
in the form x + iy.
where we have used the fact that i2 = -1, i3 = -i and i4 = 1.
Q.2. Find the three cube roots of -i. Express your answer in Cartesian form (i.e in the form x + iy)
Given z3 = -i Then z = (-i)1/3
The magnitude of -i is 1 and the principal argument is
hence
Where k = 0 ,1, 2
For, k = 1
Q.3. If z1 = 2 + i, z2 = 3 - 2i and 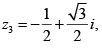 evaluate each of the following
evaluate each of the following
(i) |3z1 - 4z2|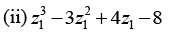
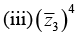
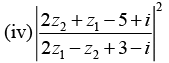
(i) |3z1 - 4z2| = |3(2 + i) - 4(3 - 2i) = |6 + 3i -12 + 8i| = |-6 + 11i|
Q.4. Find the fifth roots of -1- i.
Let z = (-1 -i)1/5
The modulus of -1- i is √2 and the argument is
k = 0 ,1, 2 , 3 , 4
Q.5. If (√3 + i)10 = a + ib, then find the values of a and b
Thus a = 29 and b = -29√3
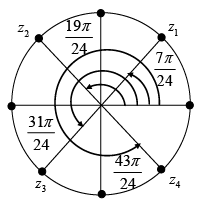
Q.6. Find the value of (-2√3 - 2i)1/4 and locate the roots graphically.
k = 0 ,1, 2 , 3
These four values are generated graphically in the figure below
Q.7. If 2 + √3 is a root of quadratic equation x2 + ax + b = 0, when a, b, ∈ R, Then find the values of a and b.
Since complex roots always occur in pairs, therefore if 2 + i√3 is a root then 2 - i√3 is also a root.
Thus, sum of roots = -a = 4 ⇒ a = -4 product of roots = b = 7
⇒ (2 + i√3)(2 - i √3) = 4 + 3 = 7 = b
thus a = -4 and b = 7.
Q.8. If n = 2 , 3 , 4 ...... prove that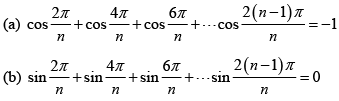
Consider the equation zn - 1 = 0 , whose solutions are the nth roots of unity.
1,e2πi/n , e4πi/n , e6πi/n ..... e2(n - 1)πi/n
We know that the sum of n roots of unity is 0. Hence
Q.9. 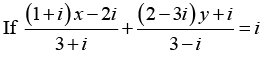
Then find the values of x and y.
Q.10. Prove that the roots of the equation 8x3 - 4x2 - 4x + 1 = 0 are cos π/7, cos 3π/7 and cos 5π/7 and hence deduce that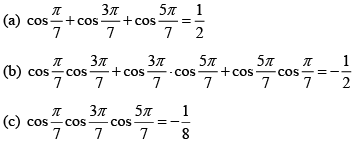
Let, y = cos θ + i sin θ, where θ has either of the values
Then, y7 = (cos 7θ + i sin 7θ) = -1i.e (y + 1) (y6 - y5 + y4 - y3 + y2 - y + 1) = 0
Now the root of y = -1 corresponds to θ = π.
The roots of the equation y6 - y5 + y4 - y3 + y2 - y + 1 = 0 ....(i)
are therefore cosθ + i sinθ , where θ has either of the values
On dividing equation (1) by y3 we obtain
⇒ 8x3 - 6x - (4x2 - 2) + 2x - 1 = 0
⇒ 8x3 - 4x2 - 4x + 1 = 0The roots of this equation are
Thus we have
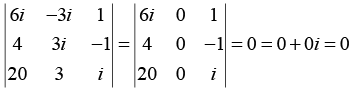
Q.11.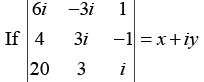
Then find the values of x and y.
Applying C2 → C2 + 3iC3 we obtain
Thus x = 0 and y = 0.
Where we have used the fact that the value of a determinant is zero if any of its row or column is zero.
Q.12. Solve the equation z2 + (2i - 3) z + 5 - i = 0
The roots of a quadratic equation az2 + bz + c = 0
Let us calculate the square roots of (-15 - 8i)
-15 - 8i = 17 [cos(θ + 2kπ) + i sin (θ + 2kπ)] where k = 0 and 1.
Where, cos θ = -15/17 and sin θ = -8/17
since θ is an angle in the third quadrant, θ/2 is an angle in the second quadrant.
Henceand the two values of (-15 - 8i)1/2 are -1 + 4i
and 1 - 4i.
Hence we can write
Q.13. If 5z2/7z1 is purely imaginary, then find the value of 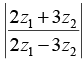 where z1 ≠ 0
where z1 ≠ 0
5z2/7z1 is purely imaginary ⇒ 5z2/7z1 = ki, where k ∈ R
Q.14. Prove that for m = 2, 3, ... 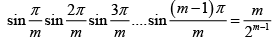
The roots of zm = are z = 1, e2πi/m , e4πi/m , e6πi/m ... e2(m-1)πi/m
Then we can write zm - 1 = (z - 1)(z - e2πi/m) (z - e4πi/m)...(z - e2(m - 1)πi/m)
Divid ing both sides by (z - 1) and then letting z = 1(realizing that
We find m = (1 - e2πi/m) (1 - e4πi/m)...(1 - e2(m - 1)πi/m) ....(i)
Taking the complex conjugate of both sides of equation (I) yields
m = (1 - e2πi/m) (1 - e4πi/m)...(1 - e2(m - 1)πi/m) ....(ii)
Multiplying (I) by (II) usingWe obtain,
Q.15. If the equation |z-i| / |z+i| = 3 represent a circle in the complex plane, then find the radius and the centre of the circle.
⇒ x2 + (y -1)2 = 9[x2 + (y + 1)2]
⇒ x2 + y2 - 2y + 1 = 9x2 + 9y2 + 18y + 9
⇒ 8x2 + 8y2 + 20y + 8 = 0
this is the equation of a circle with center atand of radius
Q.16. If |z| < 1, Then 1 + z + z2 + z3 + ... 1/(1-z). Using this fact and assuming that |a| < 1, prove the following
(a) 1 + a cosθ + a2 cos2θ + a3 cos3θ ....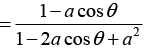
(b) a sinθ + a2 sin2θ + a3 sin3θ + ..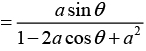
Let z = aeiθ , then since |a| < 1 we can write
⇒ (1 + a cosθ + a2 cos 2θ + ....) + i (a sinθ + a2 sin 2θ + ....)
⇒ (1 + a cosθ + a2 cos2θ +...) + i(a sinθ + a2 sin 2θ + ....)
Equating the real and imaginary parts we obtain
Q.17. Let z1 and z2 be two complex numbers such that z1 + z2 and z1z2 are both real then find the value of  denotes the complex conjugate z2.
denotes the complex conjugate z2.
Let z1 = a+ ib and z2 = c + id, then z1 + z2 is real ⇒ (a + c) + i (b + d) is real
⇒ b + d = 0 ⇒ d = -b
z1z2 in real ⇒ (ac - bd) + i (ad + bc) in real. ⇒ ad + bc = 0 ⇒ a (-b) + bc = 0 ⇒ a = c
Q.18. Find the real and Imaginary parts of
(a) e3iz
(b) cos 2z
(c) z2e2z
(d) sin h2z
(e) z coshz
(a) e3iz = e3i(x+iy) = e3ix-3y ⇒ e3iz = e-3y. e3ix = e-3y [cos 3x + i sin3x]
Thus the real and imaging parts are u(x, y) = e-3y cos 3x and v(x, y) = e-3y sin 3x.
(b) cos 2 z = cos (2 x+ 2iy)= cos 2x · cos (2iy) - sin 2x sin (2iy)
⇒ cos 2z = cos 2x cosh 2y - i sin 2x sinh 2yThus, u (x, y) = cos 2x cosh 2y
And, v (x, y) = - sin 2x sinh 2y
(c) z2e2z = (x + iy)2 e2(x + iy)
⇒ z2 e2z = (x2 + 2ixy - y2) e2x·e2iy
= z2 e2z = e2x [(x2 - y2)cos 2y - 2xy sin 2y] +ie2x[2xy cos 2y + (x2 - y2) sin 2y]
[cos 2y · sinh 2x + i sin 2y cosh 2x]u(x, y) = cos 2y sinh 2x , v (x, y) = sin 2y cosh 2x
(e)
Hence, u (x, y) = cos 2x · cosh 2y and v (x, y) = sin 2x sinh 2y= (x cosh x cos y - y sinh x sin y) + i (y cosh x cos y + x sinh x sin y)
Thus u (x, y) = cosh x cos y - y sinh x sin y and v (x, y) = y cosh x cos y + x sinh x sin y
Q.19. Find the locus of points representing the complex numbers z for which |z| - 2 = |z - i| - |z + 5i| = 0
|z| - 2 = |z - i| - |z + 5i| = 0
⇒ |z| = 2 and |z - i| = |z + 5i|
⇒ z lies on a circle |z| = 2 and the perpendicular bisector of the line segment joining (0, -5) and (0, 1) that is y = -2 putting y = -2 in |z| = 2
i.e x2 + y2 = 4 we obtain x = 0
Hence the locus of z is a single point (0, -2).
Q.20. Obtain all the values of
(a) In(√3 - i)
(b) ln (3i)
(c) ln (-√2- i√2)
(d) (1 - √2i)i
And then find the principal value in each case.
(a) ln (√3 - i)
And the principal argument is
Where n = 0, ±1, ±2, ±3 ......
The principal value of (√3 - i) is obtained when n = 0, Thus the principal value is
(b) The complex number z = 3i has modulus 3 and the principal argument π/2The principal values of ln (3i) occurs when n = 0, Thus the principal value
(c) The complex numberhas the modulus
and the principal argument
Hence the general values of
Where n = 0, ±1, ±2, ±3,......
The principal values ofis obtained when n = 0, thus the principa l values is
(d) First we find the value of
Where k = 0,1
when,
when,we obtain
whenthe principal value is
when,
the principal value is
Q.21. If (1+x)/(1-x) = cos2θ + i sin2θ, then find the value of α such that x = α tan θ.
Using componendo and dividendo we can write
Hence, the value of α is i.
Q.22. Express each of the following complex numbers in polar and Eulerian form (using the principal argument -π < arg z ≤ π).
(i) 2 + 2√3i
(ii) 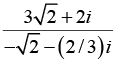
(iii) (√2 + √2i)12
(iv) (9 + 9i)3
(i) we have
Since θ lies in the first quadrant θ = α
Hence, θ = π/α,
Hence the polar form is
Eulerian form is z = eiπ/3.
(ii) GivenRationalising the denominator gives
Thus z lies on the negative x - axis and its principle argument is θ = π
Hence, r = 3 and θ = π
Hence the polar form is z = 3[cos(π) + i sin (π)]. The Eulerian form is z = 3eiπ(iii) Let z = (√2 + √2i)
Then,
Since θ lies in the first quadrant hence θ = α = π/4.Thus, in polar form
and the Eulerian form of z is z = 2eiπ/4
Using Euler’s formula
(cosθ + i sinθ)n = cos nθ + i sin nθ
We obtain
z12 = 212 [cos 3π + i sin 3π]
In terms of principle angle we can writez12 = 212 (cos π + i sin π)
The eulerian form of z12 is
z12 = 212ei(3π) = 212 eiπ(iv) Let z = 9 + 9i
Since θ lies in the first quadrant, hence θ = α = π/4.
Using the Euler’s formula, (cos θ + isin θ)n = cos nθ + i sin nθ
We can write ;
Sinceis the principal argument.
The Eulerian form of
Q.23. 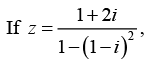 then find arg (z) (where -π < argz ≤ π).
then find arg (z) (where -π < argz ≤ π).
Since z = 1 lies on the real axis hence its principal argument is 0.
Q.24. 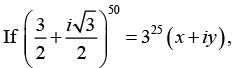 where x and y are reals then find the values of x and y.
where x and y are reals then find the values of x and y.
The Three roots of unity are
Hence we can write -(-ω)50 = (x + iy)
Since ω3 = 1 hence we can write -ω2 = (x + iy)
|
78 videos|18 docs|24 tests
|
FAQs on Complex Numbers: Assignment - Mathematical Methods - Physics
| 1. What is the importance of complex numbers in the IIT JAM exam? |  |
| 2. How can complex numbers be represented geometrically? |  |
| 3. What are the properties of complex conjugates? |  |
| 4. How are complex numbers used in solving polynomial equations? |  |
| 5. How can complex numbers be used to solve problems in electrical circuits? |  |

|
Explore Courses for Physics exam
|

|
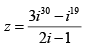
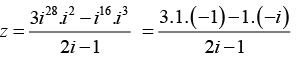
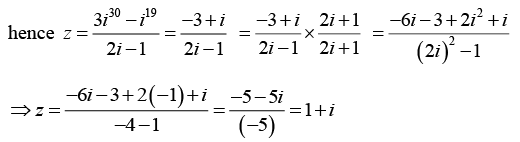
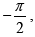 hence
hence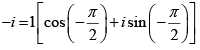
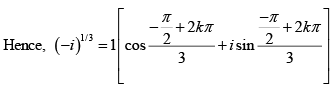
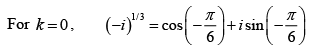
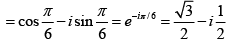
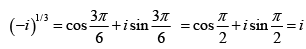
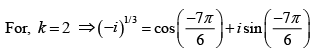
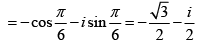
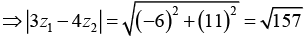

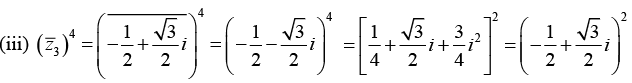
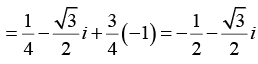
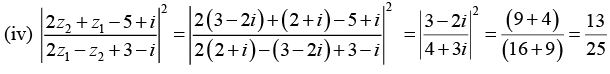

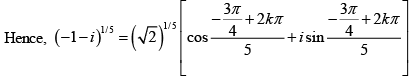
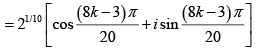
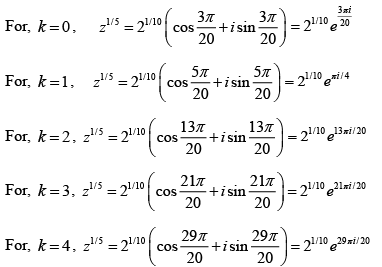
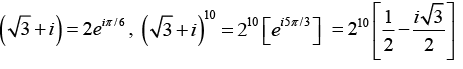
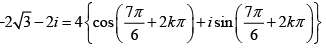
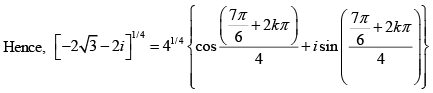
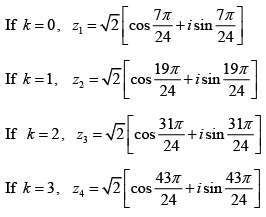
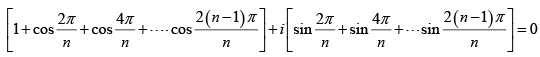
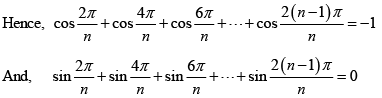
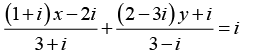

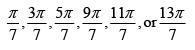
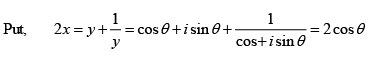
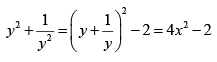
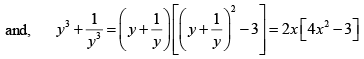
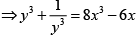
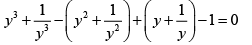
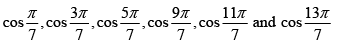
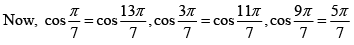
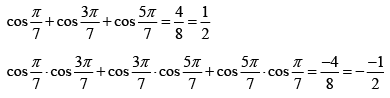
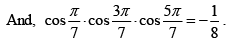
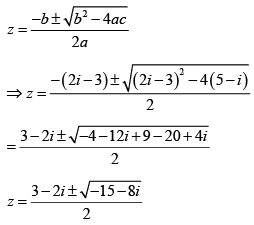
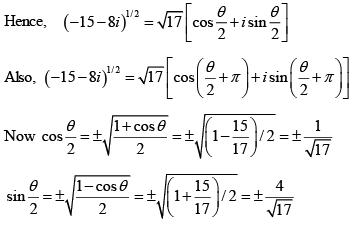
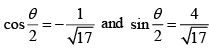 and the two values of (-15 - 8i)1/2 are -1 + 4i
and the two values of (-15 - 8i)1/2 are -1 + 4i
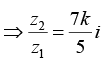
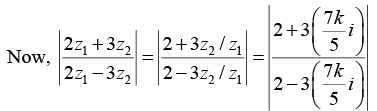

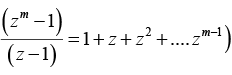
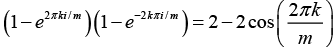
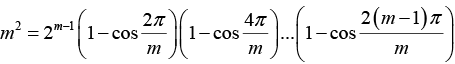
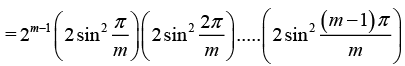

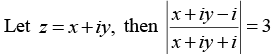
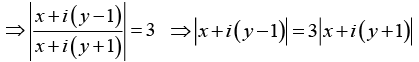
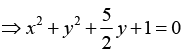
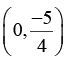 and of radius
and of radius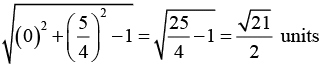
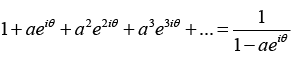
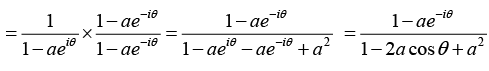
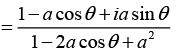
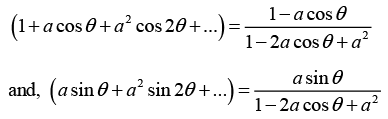
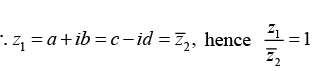
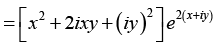
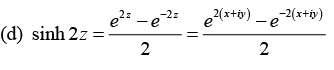

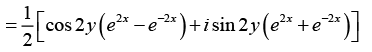
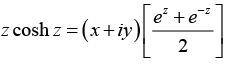
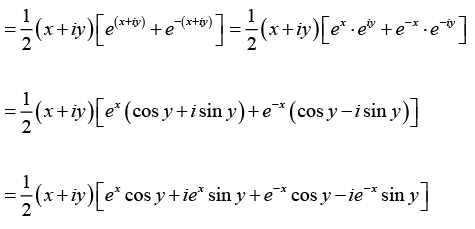
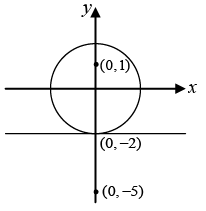
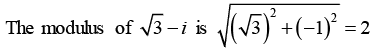
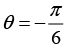
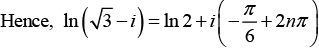
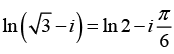

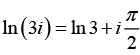
 has the modulus
has the modulus 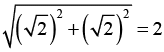 and the principal argument
and the principal argument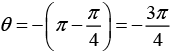
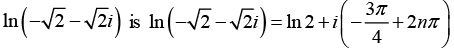
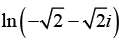 is obtained when n = 0, thus the principa l values is
is obtained when n = 0, thus the principa l values is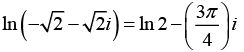
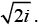
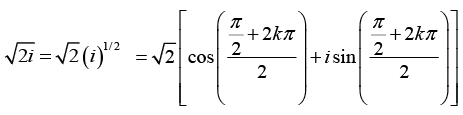
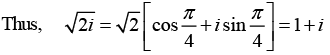
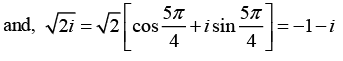
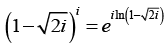
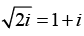
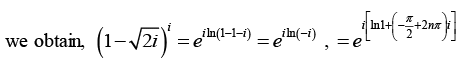
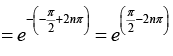
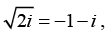 we obtain
we obtain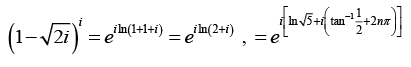
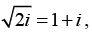 the principal value is
the principal value is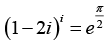
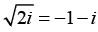 the principal value is
the principal value is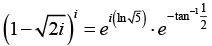
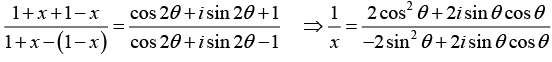
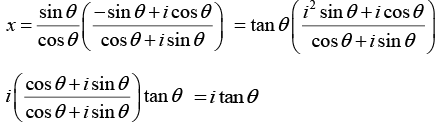
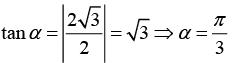

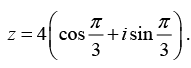
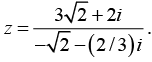
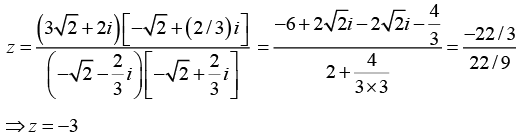
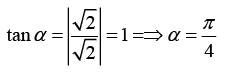
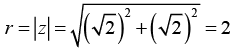
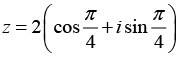
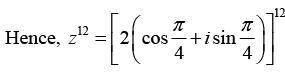

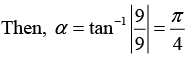
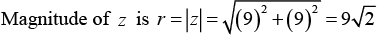
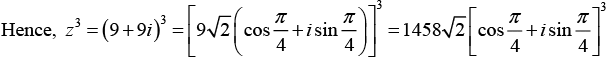
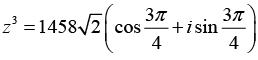
 is the principal argument.
is the principal argument.