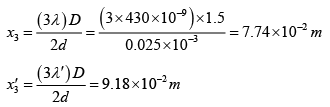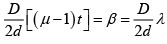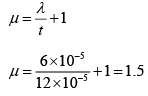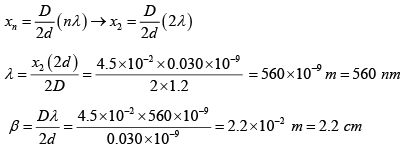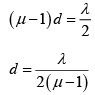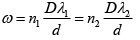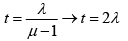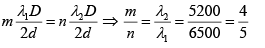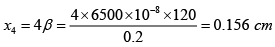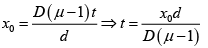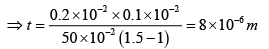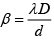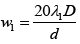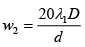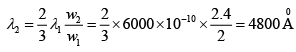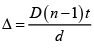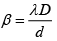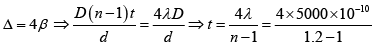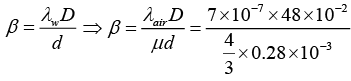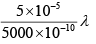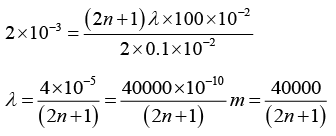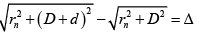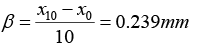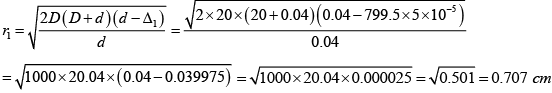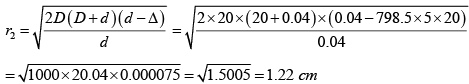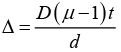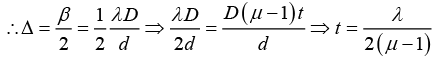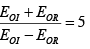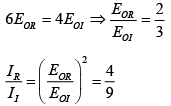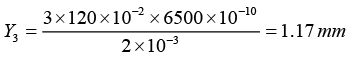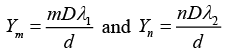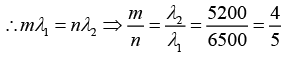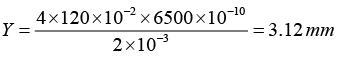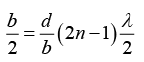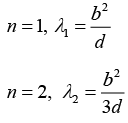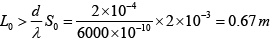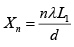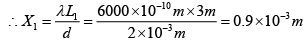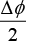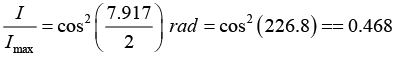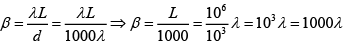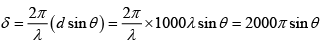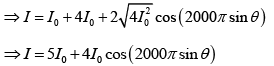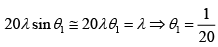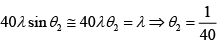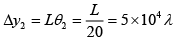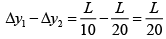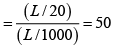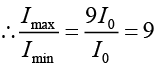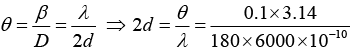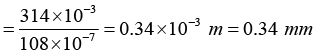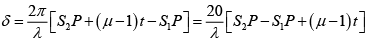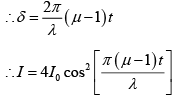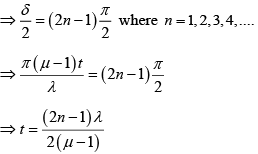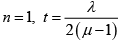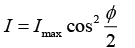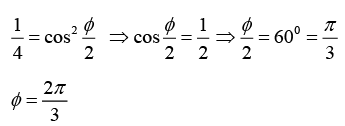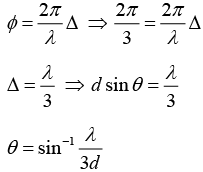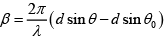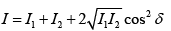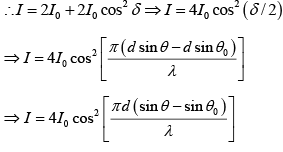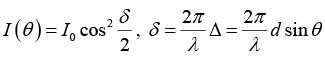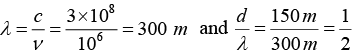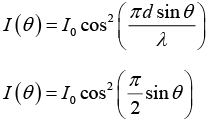Interference of Light: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. A light source emits visible light of two wavelengths λ = 430 nm and λ' = 510 nm . The source is used in a double slit interference experiment in which D = 1.5m and distance between the slits is 0.025 mm . Find the separation between third order bright fringes.
At n = 3
Δx = x'3 - x3 = 1.4 cm
Q.2. On placing a thin sheet of mica of thickness 12 x 10-5 cm in the path of one of the two interfering beams in YDSE arrangement, it is found that the central bright band shifts a distance equal to the width of a bright fringe. Find the refractive index of mica. (Given λ = 6000Å)
Q.3. A viewing screen is separated from a double slit source by 1.2 m. The distance between the two slits is 0.030 nm . The second order bright fringe (n = 2) is 4.5 cm from the central line? What will be the fringe width and wavelength of light?
n = 2, 2d = 0.030 x 10-9m, D = 1.2m, x2 = 4.5 x 10-2m
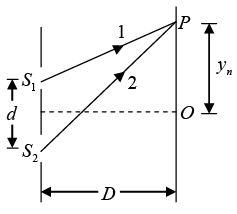
Q.4. Two transparent slabs having equal thickness but different refractive indces μ1 and μ2 are pasted side by side to form a composite slab. This slab is placed just after the double slit of YDSE, so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point which is equidistant from the slits?
To have a minimum at point P, the path difference should change by λ/2
Q.5. White light is used in a Young’s double slit experiment. Find the order of bright fringe of red light (700 nm) that will overlap with7th bright fringe of violet light (400 nm).
x = D/2d (7 x 400 x 10-9) = D/2d (n x 700 x 10-9)
= n = 4th
Q.6. In a YDSE, the slits are at a distance 2L from each other and the screen is at a distance D from the slits. If a glass slab of refractive index μ and thickness d is placed in the path of one of the beams, then calculate the minimum value of d for the central fringe to be dark.
For central fringe to be dark
Q.7. In YDSE, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600 nm is used. If the wavelength of light is changed to 400 nm, then calculate number of fringes observed in the same segment of the screen.
12 x 600 = n2 x 400 n2 = 18
Q.8. In the ideal YDSE, when a glass plate, (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength λ), the intensity at the position where the central maximum occurred previously remains unchanged. Find the minimum thickness of the glass plate.
(μ - 1) t = λ
Q.9. A beam of light consisting of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in a YDSE. The distance between the slits is 2 mm , the distance between the plane of slits and the screen is 120 cm .Then find the least distance from the central maximum when the bright fringes due to both the wavelengths coincide.
Q.10. In Young’s double-hole experiment, a thin mica sheet (n = 1.5) is introduced in the path of one of the beams. If the central fringe gets shifted by 0.2 cm, calculate the thickness of the mica sheet. Assume d = 0.1cm and D = 50 cm.
t = 8μm
Q.11. The interference pattern is obtained using a yellow light of wavelength 6000Å, in which 20 equally spaced fringes occupy 2.0 cm on the screen. On replacing the yellow source by another monochromatic source but making no other changes it is noticed that 30 fringes occupy 2.4 cm on the screen. What is the wavelength of the second source?
Fringe width
For λ1 = 6000Å; w1 = 20β where w1 = 2cm
Therefore,
for λ2 = ?, w2 = 30β where w2 = 2.4cm
Therefore,
Now
∴ λ2 = 4800Å
Q.12. A two slit Young’s interference experiment is arranged as shown in the figure; λ = 5000Å. When a thin film of a transparent material is put behind one of the slits, the zero order fringe moves to the position previously occupied by the 4th order bright fringe. The refractive index of the film is n = 1.2. Calculate the thickness of the film.
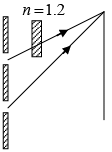
The fringe shift is
The fringe width is
Since
⇒ t = 10 x 10-6 ⇒ t = 10μm.
Q.13. A Young's double slit experiment has slits separated by 0.28 mm and a screen placed at 48 cm from the slits. The whole apparatus is immersed in water and the slits are illuminated by the red light (λ = 700 nm in vacuum). Find the fringe-width of the pattern formed on the screen. Refractive index of water is 4/3.
The wavelength in water is λw = λair/μ
The fringe width is
= 9 x 10-4m ⇒ β = 0.9mm
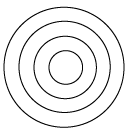
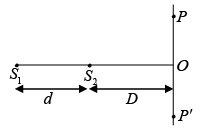
Q.14. Consider the interference pattern produced by two point sources S1 and S2 on a plane; PP' which is perpendicular to the line joining S1 and S2. Explain the nature of pattern obtained on the screen.
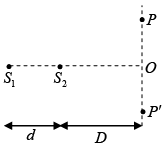
On the plane PP', the locus of the point P for which
S1P - S2P= constant will be a circle.
If S1P - S2P= nλ then one gets bright circle
If S1P - S2P = (2n + 1) λ/2 then dark circle will be observed.
If D = 20cm and S1S2 = d = 0.05 mm and π = 5000Å, then S1P - S2P = 0.05 mm = 5 x 10-5 m
S1P - S2P = 100λ
So, in the case, centre spot at 0 will be bright.
Thus one obtains Co-centric circular ring pattern on the screen.
For the used numerical values.
S2θ -S2θ= 100λ at central point
S1P - S2P= 99.5λ dark circle (first)
S1P - S2P= 99 λ first bright ring
S1P - S2P= 98.5λ second dark ring
S1P - S2P= 98 λ second bright ring
Q.15. A double slit of separation 0.1cm is illuminated by white light. A coloured interference pattern is formed on the screen 100 cm away. If a pin holes is located on this screen at a distance 2 mm from the central white fringe, which wavelength within the visible spectrum will be absent in the light transmitted through the hole. Visible spectrum lie between 3500Å and 7000Å.
Position of dark fringes
where n = 0,1, 2, 3, ....
n = 2, λ1 = 8000 Å
n = 3, λ2 = 5715.3 Å
n = 4, λ3 = 4444.4 Å
n = 5, λ4 = 3636.36 Å
Q.16. In the above question if S1P - S2P = Δ then calculate OP
Or
Calculate the radius of nth bright or dark ring in the above mentioned question.
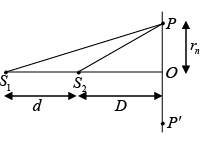
If S1P - S2P = nλ Bright ring
If S1P - S2P = (n + 1/2)λ Dark ringS1P - S2P = Δ
Q.17. In a two slit interference pattern with wavelength 6000Å, the zero order and tenth order maxima fall at 12.34 mm and 14.73 mm respectively. If wavelength is changed to 5000Å, deduce the positions of the zero order and 20th fringe; other arrangements remaining the same.
Zero order fringe is independent of λ, so it falls at 12.34 mm
x10-x0 = 10,
so position of 20th fringes
= x0 ± 20β1 = x0 ± (20 x 0.199) = 16.32 mm,8.36 mm
Q.18. For λ = 0.5μm, d = 0.4 mm and D = 200 mm, calculate the radii of first two dark rings
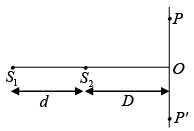
S1O - S2O= 800λ
Thus for first dark ring
S1P - S2P = Δ = 799.5λ
Calculation for first dark ring
Second dark ring
Q.19. A plate of thickness t made of a material of refractive index m is placed in front of one of the slits in a double slit experiment.
(a) Find the change in the optical path due to the introduction of the plate
(b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is λ.
(a) Path length of ray 1 = (S1P - t) + μt = S1P + (μ-1)t
∴ change in optical path = (μ-1)t
(b) The shift in the fringes is
To make zero intensity at the centre of the screen the shift Δ should be half of the fringe width β.
Q.20. A plane electromagnetic wave incident normally on the surface of a material is partially reflected. Measurements on the standing wave in the region in front of the interface show that the ratio of the electric field amplitude at the maxima and the minima is 5. Find the ratio of the reflected light intensity to the incident intensity.
Q.21. A beam of light consisting of two wavelengths, 6500Å and 5200Å is used to obtain interference fringes in Young's double slit experiment. The distance between the slit is 2.0 mm and the distance between the plane of the slits and the screen is 120 cm.
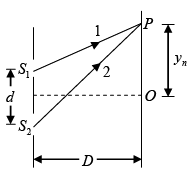
(a) Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 6500 Å.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
(a) Position of bright fringes on screen is
∴ n= 0,1, 2, 3, ....
The distance of 3rd bright fringe for λ = 6500Å is
(b) Let nth maxima of λ2 = 5200Å coincide with mth maxima of λ1 = 5200Å
Thus
Q.22. Consider the interference of two coherent electromagnetic waves whole electric field vectors are given by 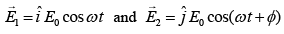 where ∅ is the phase difference. The intensity of the resulting wave is given by
where ∅ is the phase difference. The intensity of the resulting wave is given by 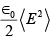 where <E2> is the time average of E2. Find the total intensity.
where <E2> is the time average of E2. Find the total intensity.
Since waves are polarized in perpendicular direction, hence there will be no interference.
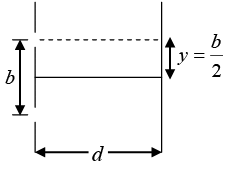
Q.23. White light is used to illuminate the two slits in YDSE. The separation between the slits is b ; and the screen is at a distance d(>b) from the slits. Show that at a point on the screen directly in front of one of the slits , wavelengths 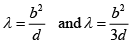 are missing.
are missing.
y = (D/d)Δ
where n = 1, 2, 3
Q.24. Consider the Young’s interference experiment as shown in the figure. Assume that the wavelength of the light is 6000Å, the slits width are all the same, S0 = S1 = S2 = 0.2 mm, the slit separation d = 2.0 mm and L1 = 30 mm.
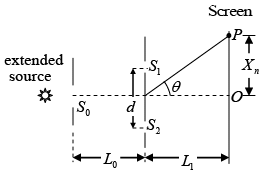
(a) About how long must L0 be in order to produce a well-defined interference pattern on the screen?
(b) What is the distance between the central and first bright fringe on the screen?
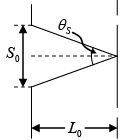
(a) The lateral length of an extended slit source is given by LS = λ/θS where θS is the angle subtended by the slit at the point concerned in radians. In order to get a clear interference pattern, the distance S1 and S2 should be less than LS, i.e. d < LS ⇒ θS < λ/d but θS = S0/L0 we require that,
(b) The position of interference maxima
Therefore, the 1st bright fringe is 0.9 mm away from the centre of the interference pattern.
Q.25. Two narrow parallel slits separated by 0.850 mm are illuminated by 600 nm light and the viewing screen is 2.8 m away from the slits, what is the phase difference between the two interfering waves on a screen at a point 2.5 mm from the central bright fringe? What is the ratio of the intensity at this point to the intensity at the center of the bright fringe?
2d = 0.850 x 10-3 m, D = 2.8 m, λ = 600 x 10-9 m
x = 2.5 x 10-3
Path difference = x(2d)/D = 7.58 x 10-7 m
Intensity I = Imax cos2
Q.26. A double-slit interference is produced by plane parallel light of wavelength l passing through two slits of unequal width, say ω1 = 20λ and ω2 = 40λ, their centre being 1000λ apart. If the observation is made on a screen very far away at L = 106λ, determine the following features
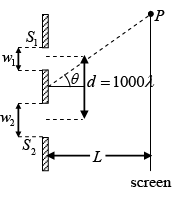
(a) Separation β between adjacent maxima and Intensity at P
(b) Width Δy1 and Δy2 of the central maxima of the diffraction patterns of the two slits individually (i.e. distance between the first zero’s)
(c) Hence, the number of fringes produced by the overlap of these central maxima.
(d) The intensity ratio between intensity maximum and minimum in the centre of the pattern.
Fringe width is
Now, as w2 = 2w1, L >> w1, w2, we may take the amplitude of the electric field vectors produced by the S1 and S2 individually on the screen to be E0 and 2F0 respectively. Since I ∝ E2, the corresponding intensities are I1 = I0 and I2 = 4I0where
(b) The diffraction intensity distribution due to a slit of width w is given by
Let the first zeroes occur at angular from the center of θ1 and θ2 given by
and
Hence the angular widths of the central maxima are
Δθ1 = 2θ1= 1/10
and Δθ2 = 2θ2= 1/20
The corresponding widths are thenand
(c) The width of the overlap of these central Maxima is
∴ The number of fringes produced by the overlap of the central maxima
(d) The intensity maximum and minimum in the centre of the pattern are given by cosδ = 1 and cosδ = -1
Q.27. In a YDSE, the angular width of a fringe formed on a distant screen is 0.10. The wavelength used is 6000Å. Calculate the spacing between the slits.
Q.28. A Young’s double slit interference produced using thin lamina sheet as shown in figure.
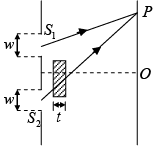 (a) What is the intensity at point O as a function of thickness t
(a) What is the intensity at point O as a function of thickness t
(b) For what value of t is the intensity at O is minimum
(c) Suppose the width w of one of the slits is now increased to 2w, the other width remaining unchanged, what is the intensity at a point O as a function of t
(a) For the double slit system, the intensity at a point on the screen is given
by I= 4I0cos2(δ/2)
where
Now, at position O, S1P = S2P
(b) The intensity at O is minimum when cos2(δ/2) = 0
For
(c) As the width of one of the slits is increased to 2w , the amplitude due to the slit will become 2E0. The intensity of the resultant wave at P is now given by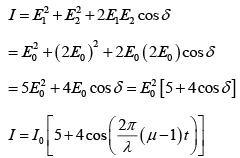
Q.29. In YDSE, find the angular position of the point at which intensity is one fourth of maximum intensity.
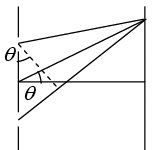
Q.30. In Young double slit interference experiment, light of wavelength λ incident at an angle θ0 on the slits S1 +S2 as shown in figure. Determine the intensity variation as a function of θ and θ0 on the screen
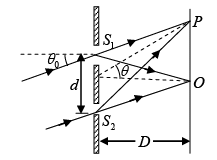
The Path difference between ray from S1 and S2 at P is Δ = d sinθ - d sinθ0
∴ Phase difference is
Now,
If two slits are of equal width, then I1 = I2 = I0
Q.31. In an interference arrangement similar to YDSE, the slits S1 and S2 are illuminated with coherent microwave sources, each of frequency 106 Hz.
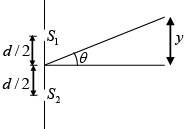 The sources are synchronized to have zero phase difference, the slits are separated by a distance d = 150m . The intensity I(θ) is measured as a function of θ, where θ is defined as shown. If I0 is the maximum intensity, then calculate I(θ) for θ = 000 ≤ θ ≤ 900 and evaluate its value at θ = 00 and θ = 300.
The sources are synchronized to have zero phase difference, the slits are separated by a distance d = 150m . The intensity I(θ) is measured as a function of θ, where θ is defined as shown. If I0 is the maximum intensity, then calculate I(θ) for θ = 000 ≤ θ ≤ 900 and evaluate its value at θ = 00 and θ = 300.
Here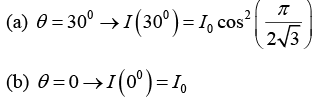
|
54 videos|22 docs|14 tests
|
FAQs on Interference of Light: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is interference of light? |  |
| 2. How does interference of light occur? |  |
| 3. What are the types of interference of light? |  |
| 4. How is interference of light useful in practical applications? |  |
| 5. Can interference of light be observed in everyday life? |  |