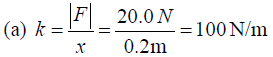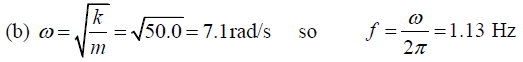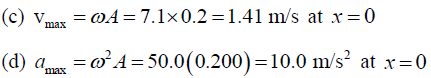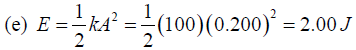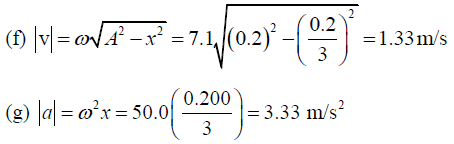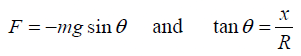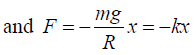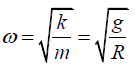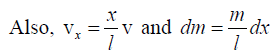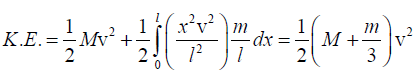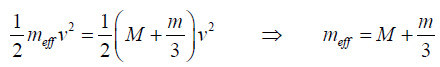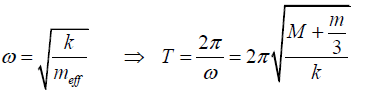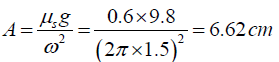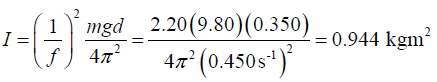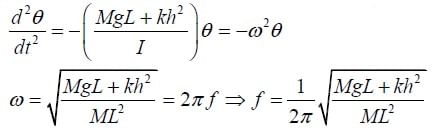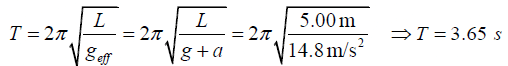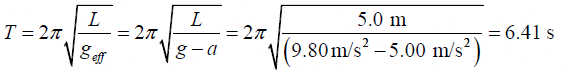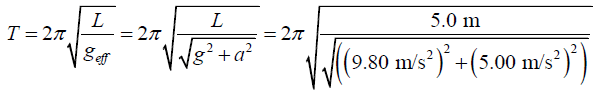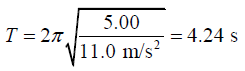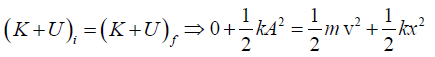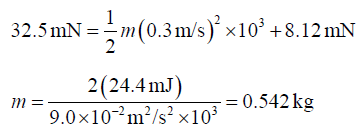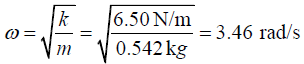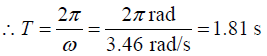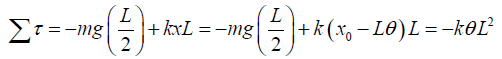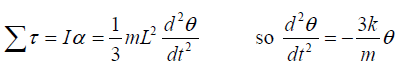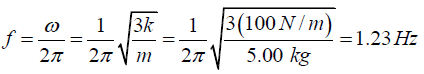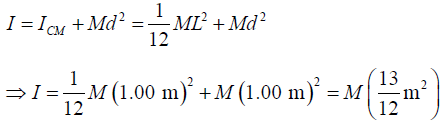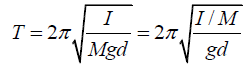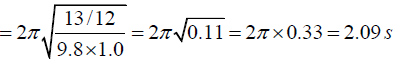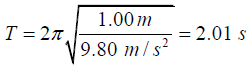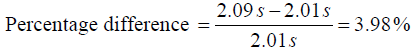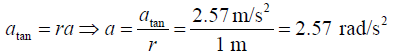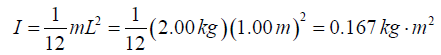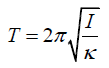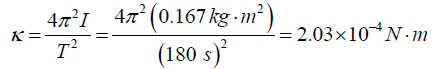Simple Harmonic Oscillator: Assignments | Oscillations, Waves & Optics - Physics PDF Download
Q.1. A 2 kg object is attached to a spring and placed on a horizontal, smooth surface. A horizontal force of 20 N is required to hold the object at rest when it is pulled 0.2m from its equilibrium position (the origin of the x axis). The object is now released from rest with an initial position of xi = 0.2m, and it subsequently undergoes simple harmonic oscillations. Find:
(a) The force constant of the spring
(b) The frequency of the oscillations
(c) The maximum speed of the object. Where does this maximum speed occur?
(d) Find the maximum acceleration of the object. Where does it occur?
(e) Find the total energy of the oscillating system.
(f) The speed and
(g) The acceleration of the object when its position is equal to one third of the maximum value.
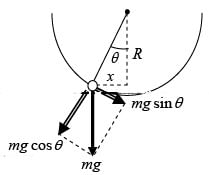
Q.2. A particle of mass m slides without friction inside a hemispherical bowl of radius R . Show that, if it starts from rest with a small displacement from equilibrium, the particle moves in simple harmonic motion with an angular frequency equal to that of a simple pendulum of length R . That is, ω = √g/R.
Referring to the sketch we have
For small displacements, tanθ ≈ sinθ
Since the restoring force is proportional to the displacement from equilibrium, the motion is simple harmonic motion
Comparing to F = -mω2x shows that
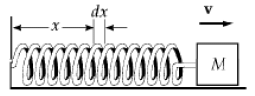
Q.3. A block of mass M is connected to a spring of mass m and oscillates in simple harmonic motion on a horizontal, frictionless track (figure). The force constant of the spring is k and the equilibrium length is l. Assume that all portions of the spring oscillate in phase and that the velocity of a segment dx is proportional to the distance x from the fixed end; that is, vx= (x/l)v. Also, note that the mass of a segment of the spring is dm = (m/ l)dx. Find
(a) the kinetic energy of the system when the block has a speed v and
(b) the period of oscillation.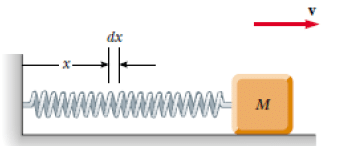
(a) For each segment of the spring, the kinetic energy is
Therefore, the total kinetic energy of the block-spring system is
(b) The kinetic energy is written as
Therefore,
Q.4. A large block P executes horizontal simple harmonic motion as it slides across a frictionless surface with a frequency f =1.50 Hz . Block B rests on it, as shown in figure and the coefficient of static friction between the two is μs = 0.600. What maximum amplitude of oscillation can the system have if block B is not to slip?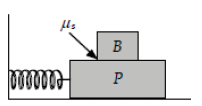
The maximum acceleration that object P achieve during oscillation is
The force corresponding to amax is
Fmax=mamax=mAω2
Where, A is the corresponding maximum amplitude of the oscillation. The object B will not slide until the Fmax does not exceed the static frictional force fstatic = μsn i.e. the condition that block B will not slip is fstatic = fmax
μsn =mAω2 ⇒ μsmg =mAω2
The maximum amplitude of oscillation can the system have if block B is not to slip is
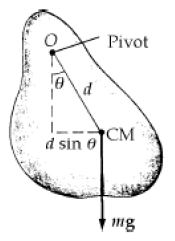
Q.5. A physical pendulum in the form of a planar body moves in simple harmonic motion with a frequency of 0.450 Hz. If the pendulum has a mass of 2.20 kg and the pivot is located 0.350 m from the center of mass, determine the moment of inertia of the pendulum about the pivot point.
Given, frequency of oscillation f = 0.450 Hz,
Length of the pendulum d = 0.350 m
And mass of the pendulum m = 2.20 kg
The time period of the compound pendulum is
Since, T = 1/f, therefore
Q.6. A pendulum of length L and mass M has a spring of force constant k connected to it at a distance h below its point of suspension (figure). Find the frequency of vibration of the system for small values of the amplitude (small θ ). Assume the vertical suspension of length L is rigid but ignore its mass.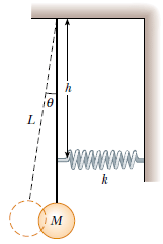
We draw a free-body diagram of the pendulum. The force H exerted by the hinge
cause no torque about the axis of rotation.
For small amplitude vibrations, use the approximations:
sinθ =θ , cosθ =1 and x ≈ s - hθ
Therefore,
Q.7. A simple pendulum is 5.00m long.
(a) What is the period of small oscillations for this pendulum if it is located in an elevator accelerating upward at 5.00m/s2 ?
(b) What is its period if the elevator is accelerating downward at 5.00 m/s2 ?
(c) What is the period of this pendulum if it is placed in a truck that is accelerating horizontally at 5.00 m/s2 ?
(a) When elevator is accelerating upward with the acceleration a, the effective
acceleration is g +a. The time of the pendulum is
(b) When elevator is accelerating upward with the acceleration a, the effective
acceleration is g - a . The time of the pendulum is
(c) When pendulum is placed in a truck that is accelerating horizontally with
acceleration a, the effective acceleration is
thus the time period of the oscillation is
Q.8. A block of unknown mass is attached to a spring with a spring constant of 6.50 N/m and undergoes simple harmonic motion with amplitude of 10.0cm. When the block is halfway between its equilibrium position and the end point, its speed is measured to be 30.0 cm/s. Calculate
(a) the mass of block
(b) the period of the motion, and
(c) the maximum acceleration of the block.
(a) Energy is conserved for the block-spring system between the maximum displacement and the half-maximum points:
(b)
(c) amax = Aω2 = 0.1m(3.46 rad/s)2 = 1.20 m/s2
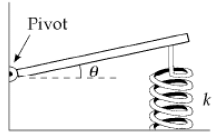
Q.9. A horizontal plank of mass m and length L is pivoted at one end. The plank’s other end is supported by a spring of force constant k (figure). The moment of inertia of the plank about the pivot is 1/3mL2. The plank is displaced by a small angle θ from its horizontal equilibrium position and released.
(a) Show that it moves with simple harmonic motion with an angular frequency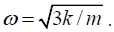
(b) Evaluate the frequency if the mass is 5.00 kg and the spring has a force constant of 100 N/m.
(a) At equilibrium, we have
where x0 is the equilibrium compression.
After displacement by a small angle,
But,
The angular acceleration is opposite in direction and proportional to the displacement, so, we have simple harmonic motion with ω2 = 3k/m.
(b)
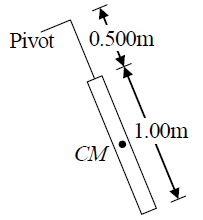
Q.10. A very light rigid rod with a length of 0.500 m extends straight out from one end of a meter stick of length 1.00 m. The stick is suspended from a pivot at the far end of the light rigid rod and is set into oscillation.
(a) Determine the period of oscillation (Use the parallel-axis theorem).
(b) By what percentage does the period differ from the period of a simple pendulum
1.00 m long?
(a) The parallel-axis theorem:
The time of oscillation is(b) The time period of the simple pendulum of length 1.00 m is
Q.11. A simple pendulum has a mass of 0.250 kg and a length of 1.00 m. It is displaced through an angle of 15.0° and then released. What are
(a) the maximum speed,
(b) the maximum angular acceleration, and
(c) the maximum restoring force?
Using the simple harmonic motion model:
(a) vmax = Aω = (0.262 m)(3.13 rad/s) = 0.820 m/s
(b) amax = Aω2 = 0.262 m (3.13 rad/s)2 = 2.57 m/s2
(c) F = ma = (0.25kg)(2.57 m/s2) = 0.641 N
Q.12. A torsional pendulum is formed by taking a meter stick of mass 2.00 kg , and attaching to its center a wire. With its upper end clamped, the vertical wire supports the stick as the stick turns in a horizontal plane. If the resulting period is 3.00 minutes, what is the torsion constant for the wire?
We suppose the stick moves in a horizontal plane. Then,
|
54 videos|22 docs|14 tests
|
FAQs on Simple Harmonic Oscillator: Assignments - Oscillations, Waves & Optics - Physics
| 1. What is a simple harmonic oscillator? |  |
| 2. What are the equations of motion for a simple harmonic oscillator? |  |
| 3. What is the period of a simple harmonic oscillator? |  |
| 4. How is the energy of a simple harmonic oscillator related to its amplitude? |  |
| 5. How does the frequency of a simple harmonic oscillator change with the mass and spring constant? |  |