Superposition Principle: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. In YDSE, the interference pattern is found to have an intensity ratio between the bright and dark fringes as 9 . Find the ratio of amplitude and intensity of interfering sources.
= 9
= 3
= 4
Q.2. A thin paper of thickness 0.02mm having refractive index 1.45 is pasted across one of the slits in Young's double slit experiment. The paper transmits 4/9 of the light falling on it.
(a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern.
(b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of light used is 600nm.
(a)
Where
∴
= 25
(b) Fringe shift due to introduction of paper of refractive index μ is
Δ =
where Δ = nβ =
⇒ n =
=
=
= 15
Q.3. The electric fields of two light sources with nearby frequencies ω1 and ω2 and wave vectors 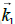 and
and 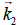 are expressed as
are expressed as  and
and 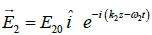 , respectively. The interference pattern on the screen is photographed at t = t0 ; denote
, respectively. The interference pattern on the screen is photographed at t = t0 ; denote 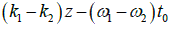 by θ . For this pattern what will be the value of cosθ for bright fringe and dark fringe. Also write the expression for maximum and minimum intensities.
by θ . For this pattern what will be the value of cosθ for bright fringe and dark fringe. Also write the expression for maximum and minimum intensities.
cosθ =+1 bright fringes
= -1 dark fringe
Q.4. In an interference pattern with two coherent sources, the amplitude of intensity variation is found to be 5% of the average intensity. Find the relative intensities of the interference sources.
= 1.051
α = 40.2
= α2 = 1616
Q.5. Two coherent sources whose intensity ratio is 81:1 produce interference pattern. Find the ratio of maximum and minimum inference of fringes.
= 9
⇒
= 100/64
=25/16
Q.6. Two coherent sources of intensity ratio β interfere. Then what will be the value of 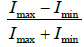 in the interference pattern.
in the interference pattern.
=

=

=
Q.7. (a) Two beams of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is π/2 at point A and π at point B. Then find the difference between the resultant intensities at A and B.
(b) In Young’s double-hole experiment, calculate 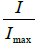 where I represents the intensity at a point where the path difference isλ / 5 .
where I represents the intensity at a point where the path difference isλ / 5 .
(a)
Intensity at position A is
Intensity at position B is
∴
(b)
Now, δ = 2π/λ (Path difference)
=
∴
= 0.66
Q.8. Two waves travelling together along the same line are represented by y1 = 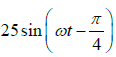 and y2 =
and y2 = 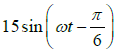 . Find
. Find
(i) the resultant amplitude
(ii) the initial phase angle of the resultant
(iii) the resultant equation for the sum of the two motions
y = y1 + y2 =
y = Asin(ωt - ∅)
where A = 39.68 and ∅ = 39.39
Q.9. Three sinusoidal waves have the same frequency with amplitude , A, A/2 and A/3 while their phase angles are 0, π/2 and π respectively. Calculate the amplitude of the resultant wave.
y1 = Asinωt
y = y1 + y2 + y3 =
=
R =
Q.10. At a given point in space the total light wave is composed of three phasors P1 = a , P2 = 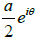 and P3 =
and P3 = 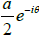 . Calculate the intensity of light at this point.
. Calculate the intensity of light at this point.
P = P1 + P2 + P3 =
=
I = P2 =
Q.11. Find the amplitude of the oscillation resulting from the addition of the following three oscillations of the same direction:
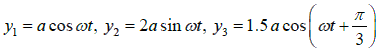
Resultant oscillation
⇒
y = Asin(ωt + θ)
A =
⇒A = 1.89a
Acosθ =
tanθ =
Q.12. In the Young’s double slit experiment the waves passing from slits S1 and S2 are described by the following pair of equations
(a) y1 = 0.5sin (3t - 4.1401) , y2 = 0.5sin (3t -7.2817)
(b) y1 = 0.5sin (6t - 2.0202) , y2 = 0.5sin (6t -8.3034)
(c) y1 = 0.5cos (9t) , y2 = 0.5sin (9t - 9.4248)
Identify the pair for which the central point on the screen is
(i) bright
(ii) dark
(iii) neither completely bright nor completely dark.
(a) Δ∅ = 3.1416 = π
Δx = λ/2 (dark)
(b) Δ∅ = 2π
Δx = λ (bright)
(c) Δ∅ = 7π/2
Δx = 7λ/4 (neither bright nor dark)
Q.13. Two similar coherent sources produce interference pattern. Find the ratio of intensity at the center of bright fringe to the intensity at a point one quarter of the distance between
two fringes from the center.
At the centre I0 = 4a2
Phase difference at a distance one quarter between the two fringes =
Intensity at that point
= 2
Q.14. In Young’s double slit experiment, the two slits act as coherent sources of equal amplitude A and wavelength λ . In another experiment with the same set-up the two slits are sources of equal amplitude A and wavelength λ , but are incoherent. Calculate the ratio of the intensity of light at the midpoint of the screen in the first case to that in the second case.
When sources are coherent Im = 4I0
When sources are incoherent I = I0 + I0 = 2I0
Ratio Im/I = 2
|
54 videos|22 docs|14 tests
|
FAQs on Superposition Principle: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is the superposition principle? |  |
| 2. How does the superposition principle apply to the IIT JAM exam? |  |
| 3. Can you provide an example of the superposition principle in quantum mechanics? |  |
| 4. How is the superposition principle useful in solving problems in quantum mechanics? |  |
| 5. Are there any limitations to the superposition principle? |  |

|
Explore Courses for Physics exam
|

|
 = 9
= 9 = 3
= 3
 = 4
= 4


 = 25
= 25 where Δ = nβ =
where Δ = nβ = 
 =
=  =
=  = 15
= 15

 = 1.051
= 1.051 = α2 = 1616
= α2 = 1616 = 9
= 9
 =
= 









 = 0.66
= 0.66















 = 2
= 2
















