Ordinary Differential Equation - Assignment | Mathematical Methods - Physics PDF Download
Q.1. x (y2 +1) dx + y (x2 +l) dy = 0, y (1) = 2
Ans. Dividing both sides by (v2 +1 y2 +1) , we have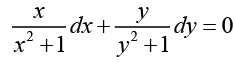
Integrating both sides gives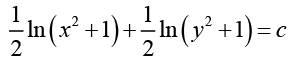
Writing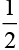 ln A in place of c1 the above solution can be written in the form
ln A in place of c1 the above solution can be written in the form
(x2+1)(y2+1) = A
Using, y (l) = 2 ⇒ (1 +1)(4 +1) = A ⇒ A = 10
Thus the required solution is (x2 +1)( y2 +1) = 10.
Q.2. (x2 - yx2) dy + (y2 + xy2) dx = 0
Ans. The given differential equation can be written as
x2 (1 - y) dy + y2 (1 + x) dx = 0
Dividing both sides by x2 y2 , we obtain 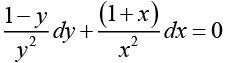
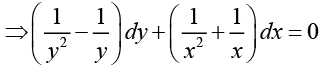
Integrating both sides gives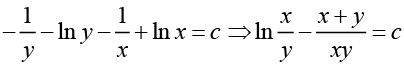
Q.3. 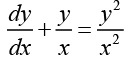
Ans. This equation can be written as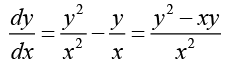
This is a homogeneous differential equation. Letting y = xv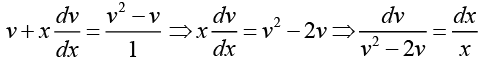
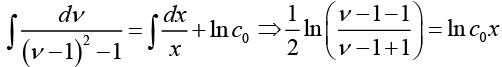
Where we have used the fact that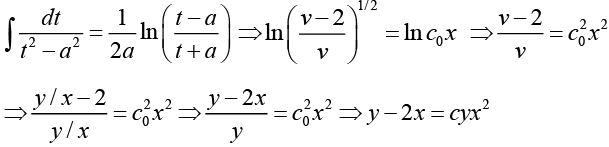
Where we have written, c02 = c .
Q.4. 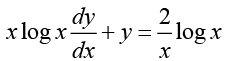
Ans. We can write,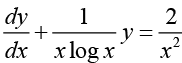
This is a linear differential equation but with integrating factor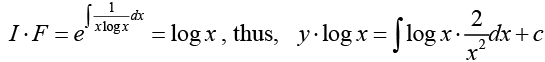
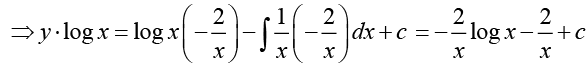
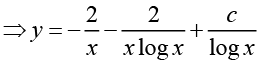
Q.5. 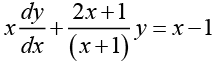
Ans. The given equation can be written as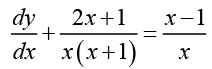
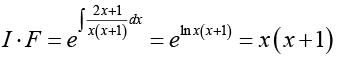
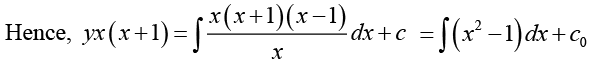
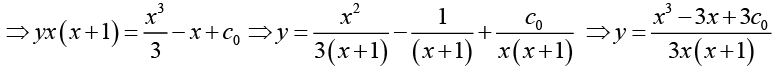
If we write c for 3c0 then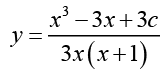
Q.6. 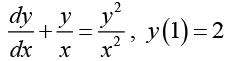
Ans. This is Bernoulli’s differential equation. Hence letting v = y1-2 = y-1 we obtain 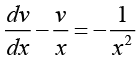
This is linear differential equation in dependent variable v and independent variable x.
Hence, 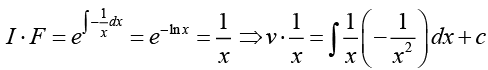
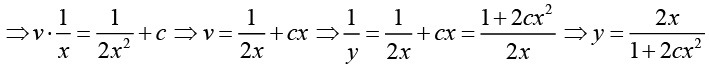
Using the given condition y (1) = 2 we obtain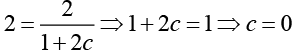
Thus, y = 2 x
Q.7. 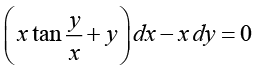
Ans. The given differential equation can be written as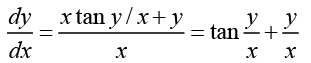
Putting, y = xv , we obtain
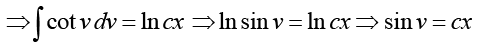
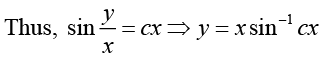
Q.8. (2y sin x cos x + y2sin x) dx + (sin2 x - 2y cos x)dy = 0 , y (0) = 3
Ans. M = 2y sin x • cos x + y2 sin x
N = sin2 x - 2 y cos x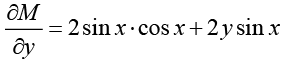
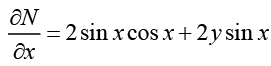
Thus the given differential equation is exact. Hence there exists a function u (x, y) such that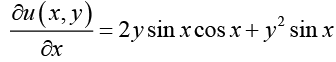 (I)
(I)
and, 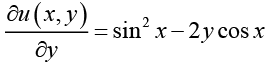 (II)
(II)
Integrating equation (I) partially with respect to x .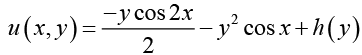 (III)
(III)
Differentiating equation (III) with respect to y , we obtain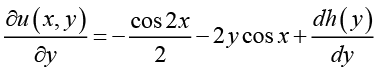 (IV)
(IV)
From equation (II) and (IV)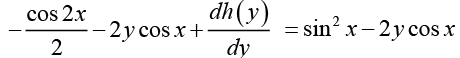

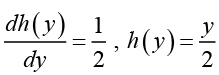
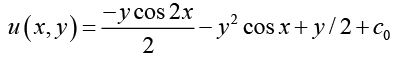
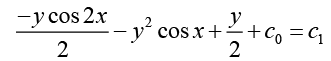
Since, y (0) = 3, c1 - 9
Hence Solution , 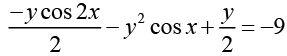
Q.9.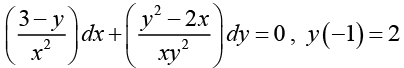
Ans.This equation is exact since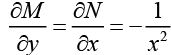
Hence there exists a function u (x, y) such that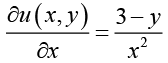 (I)
(I)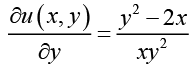 (II)
(II)
Hence using equation (I), we obtain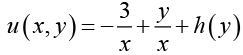 (III)
(III)
Differentiating this equation with respect to y , we obtain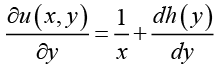 (IV)
(IV)
From equations (II) and (IV)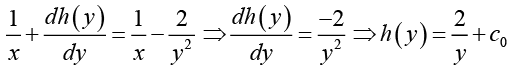
Hence the required solution is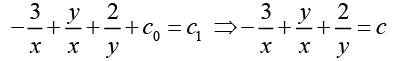
Using the given initial condition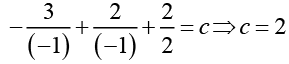
Thus the required solution is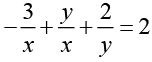
Q.10. 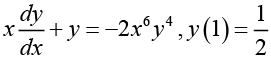
Ans. This equation can be written as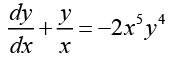
This is a Bernoulli’s differential equation.
Using, v = y1-n = y1-4 = y-3 we obtain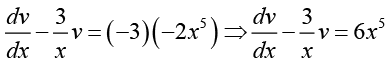
This is a linear differential equation in dependent variable v and independent variable x .
Hence, 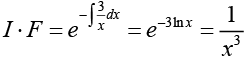
Hence, 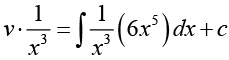
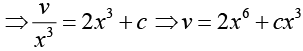
Since, 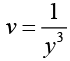 we obtain
we obtain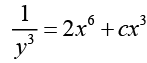
Using the given condition y (1) = 1/2
Thus the required solution is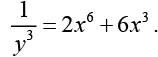
Q.11. Find the particular and general solution of the equation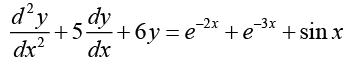
Ans. The particular solution is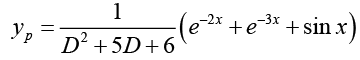
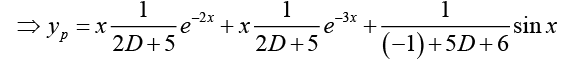
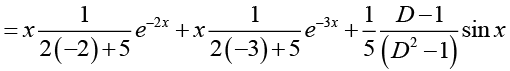
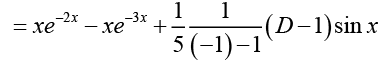
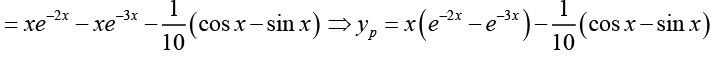
The general solution of the corresponding homogeneous differential equation is
yh = c1e-2x + c2 e-3x
Thus the general solution of the given nonhomogeneous differential equation is
y = yh + yp
⇒ y = c1e -2x + c2e -3x + x (e -2x - e -3x) -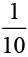 ( cos x - sin x) .
( cos x - sin x) .
Q.12. Given a differential equation (D2 - 1) y = e2x sin 2x
(a) Write the particular solution.
(b) Write the general solution.
Ans. 
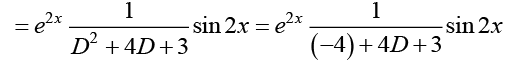
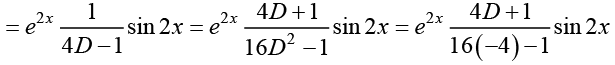
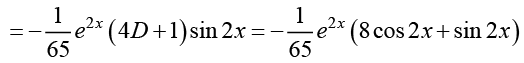
Thus, the general solution is y = c1ex + c2e -x - 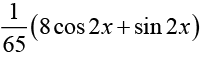
Q.13. Write the particular and general solution of (D2 + 3D + 2) y = x sin 2x
Ans. (D2 + 3D + 2) y = x sin2x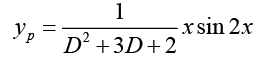
If the nonhomogeneous term r (x) of the differential equation
(D2 + aD + b y = r (x) ,
is of the form r (x) = xv (x) , then the particular solution is given by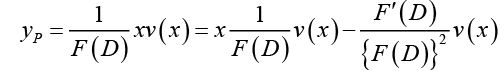
Here we see that v (x) = sin2x hence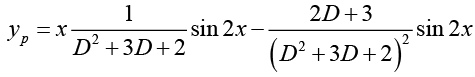

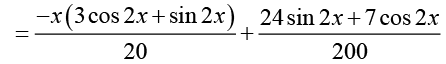
The general solution of the corresponding nonhomogeneous equation is
yh = c1e-x + c2 e-2x
hence the general solution of the given nonhomogeneous differential equation is
Q.14. Solve (D2 - 4D + 3) y = 2xex
Ans.
Thus the general solution of the given nonhomogeneous equation is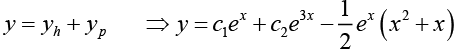
Q.15. Solve (D2 +1) y = cos2 x
Ans.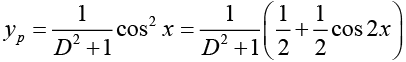
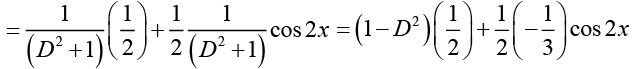
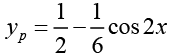
The general solution of the corresponding homogeneous differential equation is
yh = c1 cos x + c2 sin x
Hence the general solution of the nonhomogeneous equation is
y = yh + yP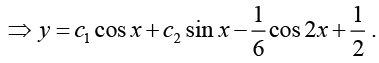
Q.16. (1 + y2) dx + (1 + x2) dy = 0, y (0) = 1
Ans. Dividing by (1 + x2) (1+y2), we get 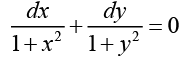
Integrating both sides gives; tan -1 x + tan -1 y = c From the given condition
From the given condition
y(0) = 1 and tan -1 0 + tan -11 = c ⇒ c = ⇒/4
Thus, tan -1 x + tan -1 y = π/4.
Q.17. sec2 x tan ydx + sec2 y tan xdy = 0
Ans. This equation is exact since 
Hence there exists a function u (x, y) such that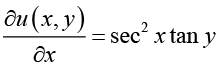 (i)
(i)
and 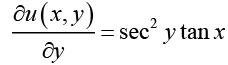 (ii)
(ii)
Integrating equation (i) partially with respect to x we get
u (x, y) = tan x • tan y + h (y ) (iii)
Differentiating it with respect to y , we obtain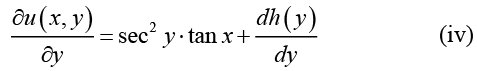
From equations (ii) and (iv)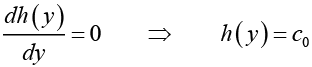
Thus, u (x, y ) = tan x tan y + c0
Hence the solution of the given differential equation is
u (x, y ) = c1 ⇒ tan x tan y = c (where c1 - c0 = c)
Q.18.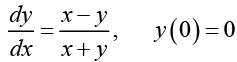
Ans. The given differential equation can be written as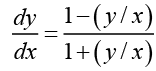
Letting y = xv, we obtain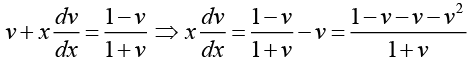
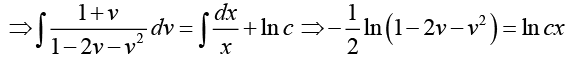
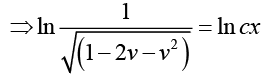
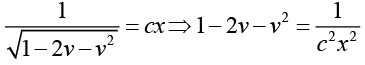
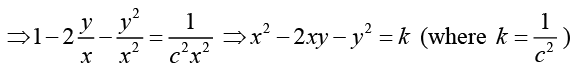
From the given condition y (0) = 0, we obtain k = 0
Thus, x2 - 2xy - y2 = 0
Q.19.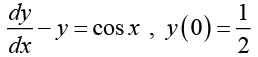
Ans. This is a linear differential equation with integrating factor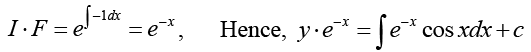 (I)
(I)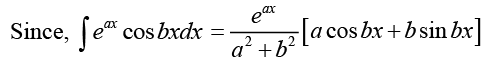
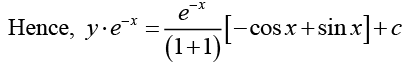
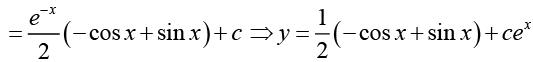
From the given condition 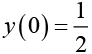
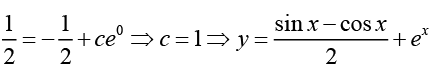
Q.20. 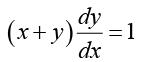
Ans. 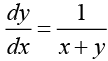
This is not a linear differential equation but when we write 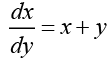
We obtain a linear differential equation 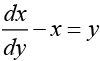
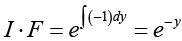
Hence the solution is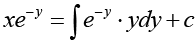
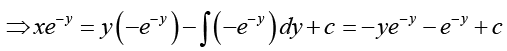
⇒ x = -( y +1) + cey
Q.21. 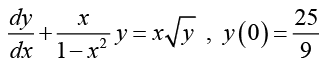
Ans. Letting v = y1 -1/2 = y1/2 , we obtain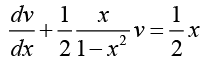
This is a linear equation in dependent variable v and independent variable x .
Hence, 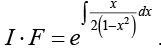
In order to evaluate the above integral we write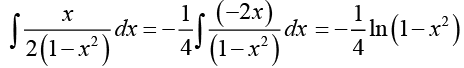
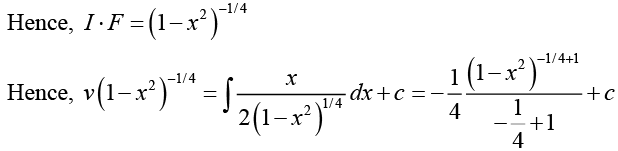
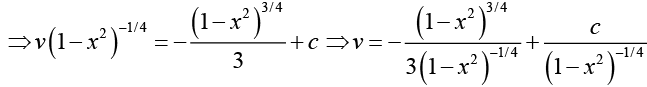
Hence, 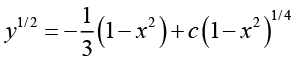
Using the given initial condition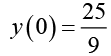
We obtain, 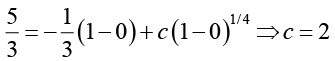
Hence, 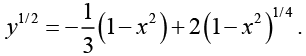
Q.22. Find the equation of the curve passing through the point (-2,3) given that the tangent to the curve at any point (x, y) is 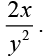
Ans. We know that the slope of tangent to any curve is 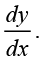
Thus, 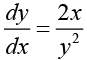
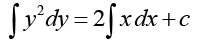

Putting the value of initial conditions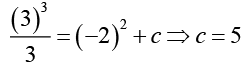
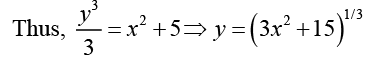
Q.23.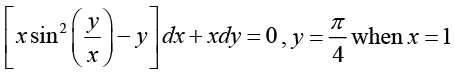
Ans. The given differential equation can be written as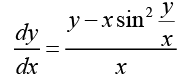
Assuming, y = xv we obtain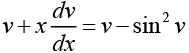
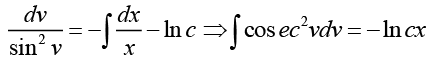
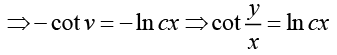
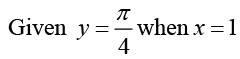

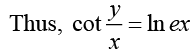
Q.24. (y sec2 x + sec x tan x) dx + (tan x + 2 y ) dy = 0
Ans. This equation is exact since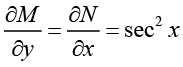
Hence the exists a function u (x, y) such that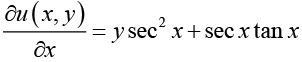 (I)
(I)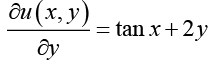 (II)
(II)
Integrating equation (I) partially with respect to x .
u (x, y) = y tan x + sec x + h (y) (III)
Differentiating equation (III) with respect to y we obtain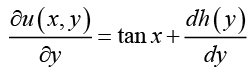 (IV)
(IV)
From equations (II) and (IV)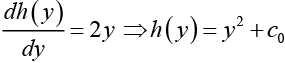
Hence, u (x, y) = y tan x + sec x + y2 + c0
Hence the required solution is
y tan x + sec x + y2 + c0 = c1 ⇒ y tan x + sec x + y2 = c
Q.25.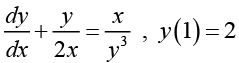
Ans. Letting v = y1-n = y1-(-3) = y4
We obtain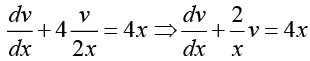
This equation is a linear differential equation in dependent variable v and Independent variable x.
Hence, 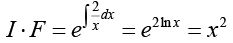
Hence, 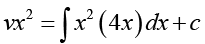
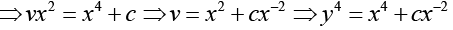
Using the given condition
y (1)=2
We obtain
16 = 1 + c ⇒ c = 15
Thus, y4 = x4 + I5x-2
Q.26. Given a nonhomogeneous differential equation
(D2-1) y = ex + e -x
(a) Find the particular solution of this differential equation.
(b) If the particular solution is written as x [f (x)] then find the value of [f'(x)2-[f (x)]2 .
Write the general solution of this differential equation.
Ans. (a) 
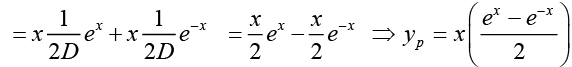
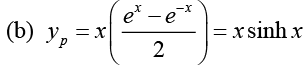
Hence f ( x) = sinh x
f'(x) = cosh x
[f'(x)]2- f(x)2 = cos2 hx - sin2 hx
⇒ [f'(x)]2 - [f(x)]2 = 1
(c) The general solution of the corresponding homogeneous differential equation
(D2 -1)y = 0 , is
yh = C1ex + C2e-x
Thus the general solution of the given nonhomogeneous equation is
y = yh + yp
⇒ y = c1ex + c2e-x + x sinh x
Q.27. Given a differential equation 
(a) Write the particular solution
(b) Write the general solution.
(c) Find the solution that passes though point (0,0) and has the slope 1 at x = 0.
Ans. (a) 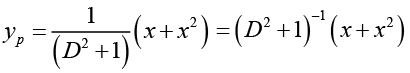
= (l + D2)- (x + x2) =(l-D2)(x + x2)
yp = x + x2 - 2
(b) Hence the general solution is
y = c1 sinx + c2 cosx + (x + x2 - 2)
(c) Given that y (0) = 0 and y'( 0) = 1
0 = c1 . 0 + c2 . 1 + (0 + 0 - 2) ⇒ C2 = 2
y' = c1 cos x - c2 sin x + (1 + 2x) ⇒ 1 = c1.1 - c2 . 0 + (1 + 2 . 0) ⇒ c1 = 0
Hence the solution with the required properties is y = 2 cos x + (x + x2 - 2)
Q.28. Find the particular and general solution of (D2 - 4) y = x2e3x
Ans. 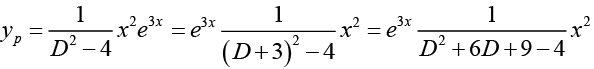
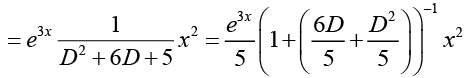
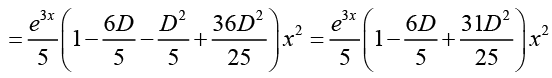
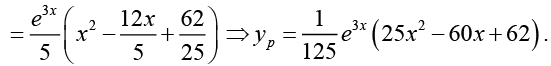
The general solution of the corresponding homogeneous equation is
yh = C1e2x + C2e-2x
Thus the general solution of the corresponding homogeneous equation is
y = yh + yp ⇒ y = cie2x + c2e-2x + 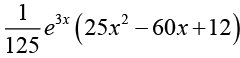
Q.29. Solve (D2 - 4D + 3) y = 3ex cos2x
Ans.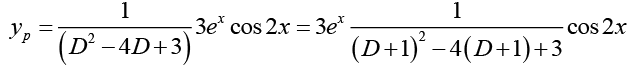
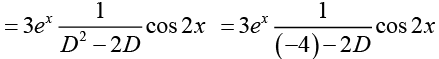
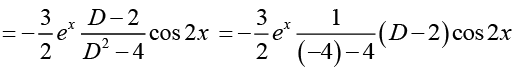
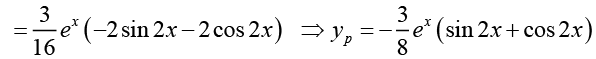
The general solution of the corresponding homogeneous differential equation is
yh = c1ex + c2 e3x
Thus the general solution of the given nonhomogeneous equation is
Q.30. Solve (D2 - 9) y = x2e4x
Ans. 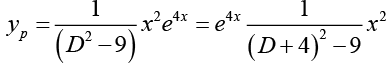
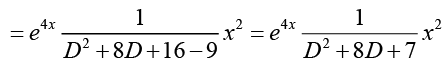
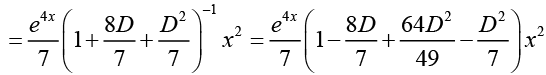
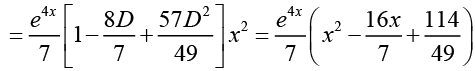
Hence, the general solution is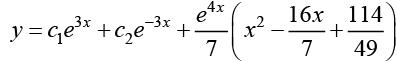
|
78 videos|18 docs|24 tests
|
FAQs on Ordinary Differential Equation - Assignment - Mathematical Methods - Physics
| 1. What is an ordinary differential equation (ODE)? |  |
| 2. What is the significance of ordinary differential equations in mathematics and physics? |  |
| 3. How are ordinary differential equations classified based on their order and linearity? |  |
| 4. What are initial value problems (IVPs) and boundary value problems (BVPs) in the context of ordinary differential equations? |  |
| 5. What are some common methods for solving ordinary differential equations? |  |
















