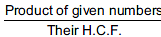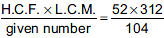Class 5 Maths Practice Question Answers - HCF and LCM
Q1: Find the H.C.F. of 15 and 28.
When you compare the prime factorization of these two numbers, you can see that there are no matching prime factors. When this is the case, it means that there are no common factors between these two numbers.
As a result, the HCF of 15 and 28 is 1.
Q2: Find all the common factors of :
(a) 24 and 40
24= 1 × 24
24 = 2 × 12,
24 = 3 × 8, 24 = 4 × 6
Therefore, all the factors of 24 are 1, 2, 3, 4, 6,
8, 12 and 24.
Also, 40 = 1 × 40, 40 = 2 × 20, 40 = 4 × 10,
40 = 5 × 8.
Therefore, all the factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40.
Thus, common factors of 24 and 40 are 1, 2, 4 and 8.
(b) 20 and 64
20 = 1 × 20, 20 = 2 × 10, 20 = 4 × 5
Therefore, all the factors of 20 are 1, 2, 4, 5, 10 and 20.
Also, 64 = 1 × 64, 64 = 2 × 32, 64 = 4 × 16, 64 = 8 × 8.
Therefore, all the factors of 64 are 1, 2, 4, 8, 16, 32 and 64.
Thus, common factors of 20 and 64 are 1, 2 and 4.
Q3: Find the H.C.F. of 18, 45 and 63.
18 = 1 × 18, 18 = 2 × 9, 18 = 3 × 6
All the factors of 18 are 1, 2, 3, 6, 9 and 18.
Also, 45 = 1 × 45, 45 = 3 × 15, 45 = 5 × 9.
All the factors of 45 are 1, 3, 5, 9, 15 and 45.
Also, 63 = 1 × 63, 63 = 3 × 21, 63 = 7 × 9.
All the factors of 63 are 1, 3, 7, 9, 21 and 63.
Common factors of 18, 45 and 63 are 1, 3 and 9.
Thus, H.C.F. of 18, 45 and 63 is 9.
Q4: Find the L.C.M. of 12 and 18.
Multiples of 12 are 12, 24, 36, 48, 60, 72, .....
Multiples of 18 are 18, 36, 54, 72, 90, .....
Thus, common multiples of 12 and 18 are 36, 72, .....
Therefore, L.C.M. of 12 and 18 is 36.
Q5: Find the first two common multiples of :
(a) 4 and 10
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, .....
Multiples of 10 are 10, 20, 30, 40, .....
Thus, the first two common multiples of 4 and 10 are 20 and 40.
(b) 5, 6 and 15.
Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 60, 65, .....
Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, .....
Multiples of 15 are 15, 30, 45, 60, 75, .....
Thus, the first two common multiples of 5, 6 and 15 are 30 and 60.
Q6: Write in the product form :
(a) 87
87 = 8 × 8 × 8 × 8 × 8 × 8 × 8
(b) 63 × 114
63 × 114 = 6 × 6 × 6 × 11 × 11 × 11 × 11.
Q7: Write in the exponential form :
(a) 5 × 5 × 5 × 5 × 5 × 5
5 × 5 × 5 × 5 × 5 × 5 = 56
(b) 8 × 8 × 8 × 8 × 9 × 9
8 × 8 × 8 × 8 × 9 × 9 = 84 × 92.
Q8: Draw a factor tree to find the prime factorisation of 96.

Thus, the prime factorisation of 96 is
= 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3.
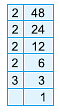
Q9: Express 56 as the product of prime factors.
We proceed as follows :

Divide 56 by 2
Divide 28 by 2
Divide 14 by 2
Divide 7 by 7
Hence, the prime factorisation of 56 is
= 2 × 2 × 2 × 7 = 23 × 7.
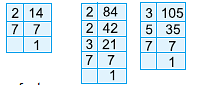
Q10: Find the H.C.F. of 14, 84 and 105.
Resolving the given numbers into prime factors, we get.
14 = 2 × 7
84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
105 = 3 × 5 × 7
H.C.F. of 14, 84 and 105 = Product of common prime factors
= Product of terms with smallest powers of common factors.
= 71 = 7
Thus, the H.C.F. of 14, 84 and 105 = 7.
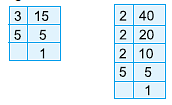
Q11: Find the H.C.F. of 28 and 72 by prime factorisation method.

Resolving each of the given numbers into prime factors, we get
28 = 2 × 2 × 7 = 22 × 7
72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
H.C.F. of 28 and 72 = Product of common prime factors
= Product of terms with smallest powers of common factors
= 22
= 4
Thus, H.C.F. of 28 and 72 = 4.
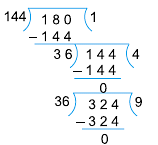
Q12: Find the H.C.F. of 144, 180 and 324.
We first find the HCF of any two numbers (144 and 180).
Since, last divisor is 36, so 36 is the HCF of 144 and 180.
Now, we find the HCF of 36 and 324.
Hence, HCF of 144, 180 and 324 is 36.
Q13: Find the L.C.M. of 16, 48 and 64.
Resolving each of the given numbers into prime factors, we get
16 = 2 × 2 × 2 × 2 = 24
48 = 2 × 2 × 2 × 2 × 3 = = 24 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2 = 26
The different prime factors of 16, 48 and 64 are 2 and 3.
Thus, L.C.M. of 16, 48 and 64 = Product of terms containing highest powers of 2 and 3.
= 26 × 3
= 64 × 3 = 192.
Q14: Find the L.C.M. of 15 and 40, using prime factorisation method.
Resolving the given numbers into prime factors, we get
So, 15 = 3 × 5
Also, 40 = 2 × 2 × 2 × 5 = 23 × 5.
The different prime factors of 15 and 40 are 2, 3 and 5.
L.C.M. of 15 and 40 = Product of terms containing highest powers of 2, 3 and 5
= 23 × 3 × 5 = 8 × 3 × 5 = 120.
Q15: Find the LCM of 18, 36 and 42 by long division method.
So, LCM of 18, 36 and 42
= 2 × 3 × 3 × 2 × 7 = 252
Hence, LCM of 18, 36 and 42 = 252.
Q16: The product of two numbers is 867 and their HCF is 17. Find their L.C.M.
We know that:
LCM =
= 867/17 = 51
Hence, the LCM of given numbers is 51.
Q17: The H.C.F. of two numbers is 52 and their L.C.M is 312. If one of the numbers is 104, find the other.
It is given here that:
H.C.F. = 52, L.C.M. = 312 and one number = 104
The other number =
= 156
Hence, the other number is 156.
Q18: Sam can jump 4 steps at a time and Nina can jump 5 steps at a time. On which of the steps will both meet if both start jumping together?
Let's find the multiples of both 4 and 5:
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, ...
Multiples of 5: 5, 10, 15, 20, 25, 30, ...
The first step where both Sam and Nina will meet is at 20 steps. This is because 20 is the first common multiple of both 4 and 5.
So, if both Sam and Nina start jumping together, they will meet on the 20th step.
Q19: Shane wants to plant 28 marigold plants and 36 rose plants in his garden. What is the greatest number of rows possible if each row has the same number of marigold plants and the same number of rose plants.
Shane wants to plant 28 marigold plants and 36 rose plants, and he wants to have the same number of plants in each row.
We need to find the greatest number of plants that can be in each row and still divide both 28 and 36 evenly.
The largest number that can divide both 28 and 36 is the Highest Common Factor (HCF).
Let's find the HCF of 28 and 36:
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
The largest number that is common to both lists is 4.
So, Shane can plant 4 marigold plants and 4 rose plants in each row.
Now, let's find the number of rows:
For marigold plants: 28 ÷ 4 = 7 rows
For rose plants: 36 ÷ 4 = 9 rows
So, the greatest number of rows Shane can have is 7 rows, and in each row, there will be 4 marigold plants and 4 rose plants.
Q20: Mary has a dance class every 2nd day and painting class every 3rd day. On which of the day will she have both the classes?
Mary has a dance class every 2nd day and a painting class every 3rd day. To find out on which day she will have both classes, we need to find the common multiples of 2 and 3.
Let's list the days for both classes:
Dance class days: 2, 4, 6, 8, 10, ...
Painting class days: 3, 6, 9, 12, ...
Now, let's find the first common day:
The common multiples of 2 and 3 are 6, 12, 18, ...
So, Mary will have both dance and painting classes on the 6th day. On the 6th day, it's a day when she has both classes - she goes to her dance class (every 2nd day) and her painting class (every 3rd day).
|
58 videos|122 docs|40 tests
|
FAQs on Class 5 Maths Practice Question Answers - HCF and LCM
| 1. What is the HCF (Highest Common Factor)? |  |
| 2. What is the LCM (Least Common Multiple)? |  |
| 3. How can I find the HCF of two numbers? |  |
| 4. Is the HCF always smaller than or equal to the LCM of two numbers? |  |
| 5. Can the HCF of two numbers be 1? |  |

|
Explore Courses for Class 5 exam
|

|