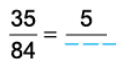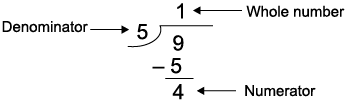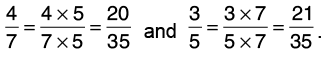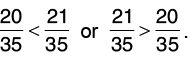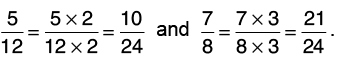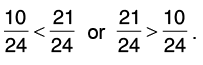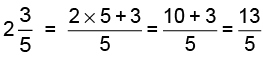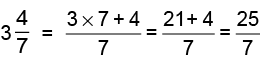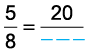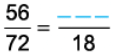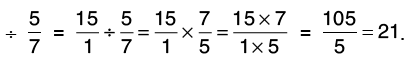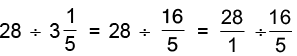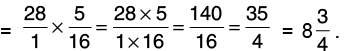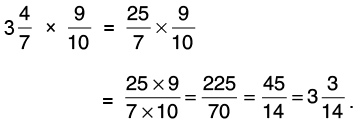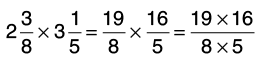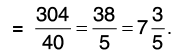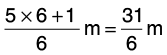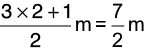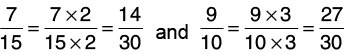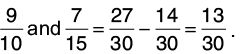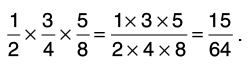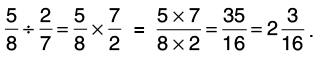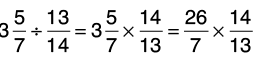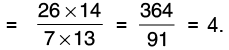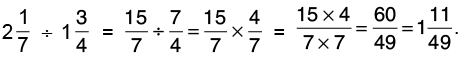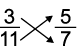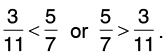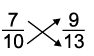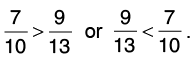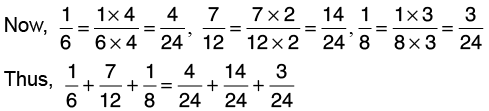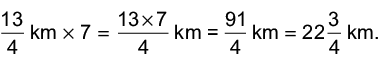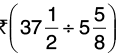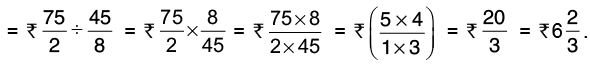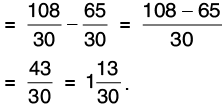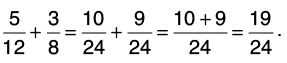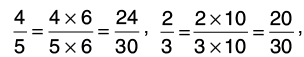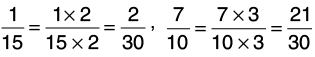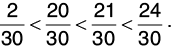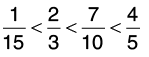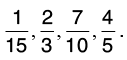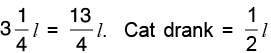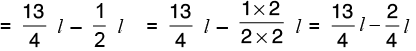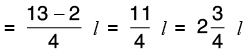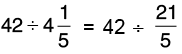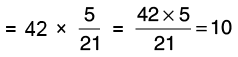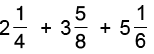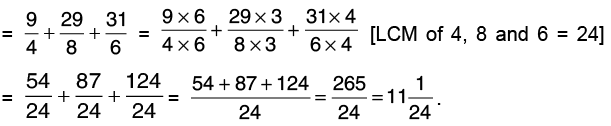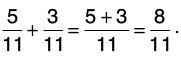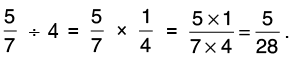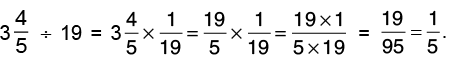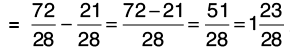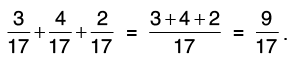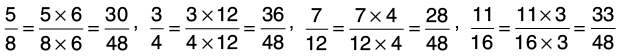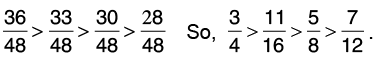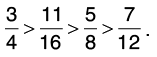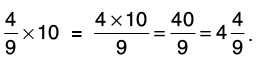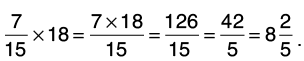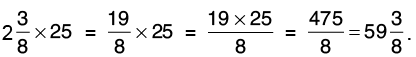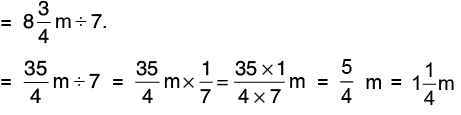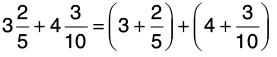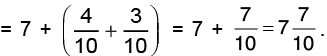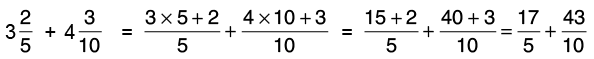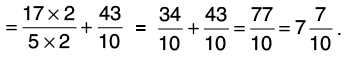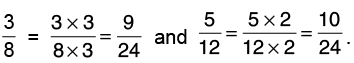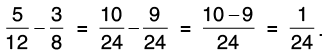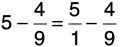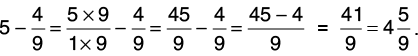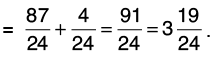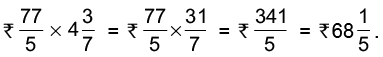Class 5 Maths - Fractions - Question Answers
Q1: Simplify:
(a) 40/75
40 = 2 × 2 × 2 × 5 75 = 3 × 5 × 5
Thus, H.C.F. of 40 and 75 is 5.Now, 40/75 = 40 ÷ 5/75 ÷ 5 = 8/15
Thus, the simplest form of 40/75 is 8/15
(b) 27/90
27 = 3 × 3 × 3 90 = 2 × 3 × 3 × 5
Thus, H.C.F. of 27 and 90 = 3 × 3 = 9.
Now, 27/90 = 27 ÷ 9/90 ÷ 9 = 3/10
Thus, the simplest form of 27/90 is 3/10
Q2: Replace the blanks in 35/84 = 5/? by the correct number.
Since, 35 ÷ 7 = 5, so we divide 35 by 7 and also 84 by 7. 35
35/84 = 35 ÷ 7/84 ÷ 7 = 5/12
Thus, 35/84 = 5/12.
Q3: Convert each of the following improper fractions into mixed numbers.
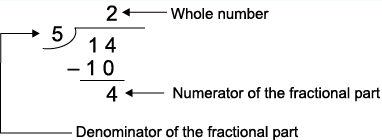
(a) 14/5
Thus, 14/5 = 2(4/5)
(b) 9/5
Thus, 9/5 = 1(4/5)
Q4: Compare
(a) 4/7 and 3/5
Given fractions are 4/7 and 3/5.
Let us now find the L.C.M. of 7 and 5.
L.C.M. of 7 and 5 = 7 × 5 = 35.
Now,
Now, compare 20/35 and 21/35
Since 20 < 21 or 21 > 20, therefore,
Hence, 3/5 > 4/7.
(b) 5/12 and 7/8
Given fractions are 5/12 and 7/8
Let us now find the L.C.M. of 12 and 8.
12 = 2 × 2 × 3, 8 = 2 × 2 × 2
So, L.C.M. of 12 and 8 = 2 × 2 × 2 × 3 = 24.
Now,
Now, compare 10/24 and 21/24.
Since, 10 < 21 or 21 > 10, therefore,
Hence, 7/8 > 5/12.
Q5: Check whether the following pairs of fractions are equivalent or not :
(a) 6/13 and 30/65
[Cross multiply]
6 × 65 = 390, 13 × 30 = 390. Both the products are equal.
Thus, 6/13 and 30/65 are equivalent.
(b) 7/12 and 42/70
[Cross multiply]
7 × 70 = 490, 12 × 42 = 504. Products are not equal.
Thus, 7/12 and 42/70 are not equivalent.
Q6: Express each of the following mixed numbers as an improper fraction.
(a) 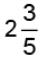
(b) 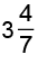
Q7: Is the fraction 16/21 in its lowest terms?
H.C.F. of 16 and 21 is 1.
Hence, the fraction 16/21 is in its lowest terms.
Q8: Find an equivalent fraction of 5/8 with numerator 20.
To get 20 in the numerator, we multiply 5 by 4 and also 8 by 4.5/8 = 5 x 4/8 x 4 = 20/32
Thus, 5/8 = 20/32
Q9: Is the fraction 20/35 in its lowest terms?
H.C.F. of 20 and 35 is 5.
Hence, the fraction 20/35 is not in its lowest terms.
Q10: Find an equivalent fraction of 56/72 with denominator 18.
To get 18 in the denominator, we divide 72 by 4 and also, 56 by 4.
56/72 = 56 ÷ 4/72 ÷ 4 = 14/18
Thus, 56/72 = 14/18.
Q11: Divide:
(a) 15 by 5/7
Reciprocal of 5/7 is 7/5
Thus, 15
(b) 28 by 3(1/5)
Reciprocal of 3(1/5) = Reciprocal of 16/5 = 5/16.
Thus,
Q12: Find the product:
(a) 4/11 x 5/9
(b) 3(4/7) by 9/10
(c) 2(3/8) x 3(1/5)
Q13: Preeti had one rope of 5(1/6) m length and another of 3(1/2) m length. How much length of rope did Preeti have in all?
Length of one rope = 5(1/6) m =
Length of another rope 3(1/2) m =
Total length of the two ropes =[L.C.M. of 6 and 2 = 6]
Hence, Preeti has 8(2/3) m rope in all.
Q 14: Find the difference between 7/15 and 9/10.
L.C.M. of 15 and 10 is 30.
Now,
Hence, 27/30 > 14/30
Hence, the difference of
Q15: Find the product of 1/2 x 3/4 x 5/8
Q16: Divide:
(a) 5/8 by 2/7
Reciprocal of 2/7 is 7/2.
Thus,
(b) 3(5/7) by 13/14
Reciprocal of 13/14 is 14/13
Thus,
(c) Reciprocal of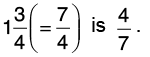
Thus,
Q17: Compare
(a) 3/11 and 5/7
Given fractions are 3/11 and 5/7.
Cross multiplyNow, 3 × 7 = 21 and 11 × 5 = 55.
Since, 21 < 55, hence,
(b) 7/10 and 9/13
Cross multiply
Now, 7 × 13 = 91 and 10 × 9 = 90.
Since, 91 > 90, hence,
Q18: Add 1/6, 7/12, and 1/8.
L.C.M. of 6, 12 and 8 is 24.
(Changing to its lowest terms)
Q19: Alka walks 3(1/4) km in 1 hour. How far does she go in 7 hours?
Distance covered in hour = 3(1/4) km = 13/4 km.
Distance covered in 7 hours =
Hence, Alka goes 22(3/4) km in 7 hours.
Q20: The cost of 5(5/8) litres of milk is Rs 37(1/2). What is the cost of 1 litre of milk?
Cost of 5(5/8) litres of milk = Rs 37(1/2)
The cost of 1 litre of milk =
Hence, the cost of 1 litre of milk is 6(2/3).
Q21: Subtract 2(1/6) from 3(3/5).
[Changing the mixed numbers into improper fractions]
[L.C.M. of 5 and 6 = 30]
Q22: Add 5/12 and 3/8.
Let us find the L.C.M. of 12 and 8. L.C.M. of 12 and 8 = 24.
Now,
Thus,
Q23: Arrange the following fractions in ascending order.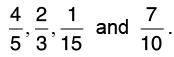
Let us find the L.C.M. of the denominators of the given fractions:
5 = 1 × 5, 3 = 1 × 3, 15 = 3 × 5, 10 = 2 × 5Thus, L.C.M of 5, 3, 15 and 10 = 2 × 3 × 5 = 30.
Now, we change each of the given fractions into equivalent fractions with denominator 30.
Clearly, 2 < 20 < 21 < 24, so,
Hence
Hence, the ascending order is
Q24: A vessel had 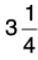 litres of milk. A cat drank 1/2 litres. How much milk is left in the vessel?
litres of milk. A cat drank 1/2 litres. How much milk is left in the vessel?
Milk in the vessel =
Milk left in the vessel
Hence,of milk is left in the vessel.
Q25: Shyam has Rs 42. He wants to buy chocolates from that money. If the cost of each chocolate is Rs 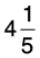 , how many chocolates can he buy?
, how many chocolates can he buy?
Cost of 1 chocolate = Rs 4(1/5)
Amount of money Shyam has = Rs 42
Number of chocolates Shyam can buy =
Hence, Shyam can purchase 10 chocolates for Rs 42.
Q26: Add 2(1/4), 3(5/8) and 5(1/6).
[Changing the mixed numbers into improper fractions]
Q27: Add 5/11 and 3/11.
Q28: Divide:
(a) 5/7 by 4
Reciprocal of 4 is 1/4.
Thus,
(b) 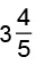 by 19.
by 19.
Reciprocal of 19 is 1/19.
Thus,
Q29: Subtract 3/4 from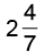 .
.
[Changing 2(4/7) into an improper fraction]
[L.C.M. of 7 and 4 = 28]
Q30: Add 3/17, 4/17 and 2/17.
Q31: Arrange the following fractions in descending order. 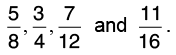
Let us find the L.C.M of the denominators of the given fractions:
8 = 2 × 2 × 2, 4 = 2 × 2, 12 = 2 × 2 × 3, 16 = 2 × 2 × 2 × 2
L.C.M. of 8, 4, 12 and 16 = 2 × 2 × 2 × 2 × 3 = 48.
Now, change each of the given fractions into equivalent fractions with denominator 48.
Clearly, 36 > 33 > 30 > 28.
Thus,
Hence, the descending order is
Q32: Multiply:
(a) 4/9 by 10
(b) 7/15 by 18.
(c) 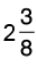 by 25
by 25
Q33: Swati had 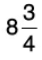 m long rope. She cut it into 7 equal parts. Find the length of each piece of the rope.
m long rope. She cut it into 7 equal parts. Find the length of each piece of the rope.
Length of the rope =
m.
Number of pieces cut out = 7Length of each piece
Hence, the length of each piece of the rope = 1(1/4) m.
Q34: Add 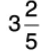 and
and 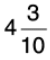
[Add whole numbers and fractions separately]
[L.C.M. of 5 and 10 = 10]
Another method: Change the mixed numbers into improper fractions and add.
Q35: Find the reciprocal of:
(a) 9
(b) 7/8
(c) 4/15
(d) 3(4/7)
(a) Reciprocal of 9 = 1/9
(b) Reciprocal of 7/8 = 8/7
(c) Reciprocal of 4/15 = 15/4.
(d) 3(4/7) = 25/7
Reciprocal of 25/7 = 7/25
Q36: Subtract 3/8 from 5/12
Let us find the L.C.M. of 8 and 12.
L.C.M. of 8 and 12 = 24.
Now,
Hence,
Q37: Add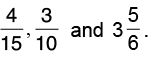
[Changing 3(5/6) into an improper fraction]
[L.C.M. of 15, 10 and 6 = 30]
[Changing into its lowest terms]
Q 38: Subtract 4/9 from 5.
We write the whole number as a fraction by putting 1 in the denominator.
Clearly,
Now, L.C.M. of 1 and 9 = 9.
Hence,
Q39: Add 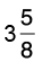 and 1/6.
and 1/6.
[Changing 3(5/8) into an improper fraction]
[L.C.M. of 8 and 6 = 24]
Q40: The cost of 1 m of cloth is 15(2/5). Find the cost of 4(3/7) m of cloth.
Cost of 1 m of cloth = Rs 15(2/5) = Rs 77/5
Cost of 4(3/7) m of cloth =
Hence, the cost of 4(3/7) m of cloth = Rs 68(1/5).
|
56 videos|187 docs|40 tests
|
FAQs on Class 5 Maths - Fractions - Question Answers
| 1. What are fractions and how are they used in everyday life? |  |
| 2. How do you add and subtract fractions with different denominators? |  |
| 3. What is the difference between proper, improper, and mixed fractions? |  |
| 4. How do you multiply and divide fractions? |  |
| 5. What are equivalent fractions and how do you find them? |  |