Application of Quantum Mechanics in Cartesian Coordinate: Assignment | Modern Physics PDF Download

Q.1. The needle on a broken car speedometer is free to swing, and bounces perfectly off the pins at either end, so that if you give it a flick it is equally likely to come to rest at any angle between 0 and π
(a) What is the probability density, f (θ) ?
(b) Compute (θ),(θ²) and σ =Δθ , for this distribution

f (θ) =A ,0 <θ < π

Q.2. (a) If  φ( θ,φ)  = A  find the value of A such that φ₁( θ,φ) is normalized.
(b)  Prove that 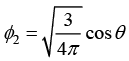 is orthogonal to φ₁

The wave function φ₁( θ,φ) = A is defined in spherical symmetry variable is solid angle

Q.3. Consider the function  where λ and ω are constant. Find the value of A such that ψ(x, t ) is normalized.

Q.4. if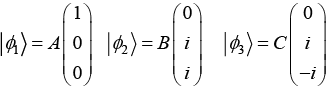
(a) Find normalization constant A, B, C for ket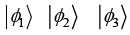
(b) Prove that 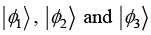 are orthogonal
(c) Check whether 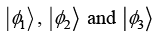 are linearly independent or not.
(d) Write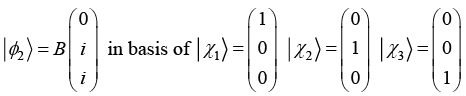
(e) 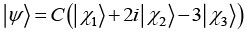 then find value of C such that |ψ⟩ is normalized
(f) If operator A is defined as A |χ_n⟩ ₌ na|χ_n⟩ where n = 1, 2, 3... then find value of A |ψ⟩
(g) If operator A is defined as A |χ_n⟩ ₌ na|χ_n⟩ where n = 1, 2, 3... then find value of ⟨ χ₂|A |ψ⟩
(h) If operator A is defined as A |χ_n⟩ ₌ na|χ_n⟩ where n = 1, 2, 3... then find value of ⟨ ψ|A |ψ⟩

then

(a)


(b)
 

(c)

c₁ = 0 c₂ +c₃= 0 and c₂ -c₃= 0 ⇒ c₁ = 0,c₂ = 0,c₃ = 0
So |ϕ₁⟩, |ϕ₂⟩ and |ϕ₃⟩ are linearly independent
(d)


 in basis of  

(e)


(f)




(g)


(h)

Q.5. Consider the Gaussian probability distribution 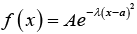 where -∞ < x < ∞ where A, a and λ are positive real constants.
(a) Determine A such that f(x) is probability density
(b) Find ⟨x⟩, ⟨x²⟩  and σ =Δx
(c) Sketch the graph of f (x)

(a)






(c)

Q.6. If 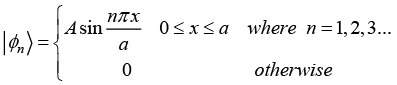, then
(a)  Find the value of A such that | ϕ_n⟩ is normalized
(b) ⟨ϕ_m|ϕ_n⟩ = δ_m,n
(c) If H operator is defined as  then  prove that the matrix element 

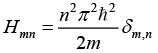
(a)



(b)




=
For m =n


(c)