Special Theory of Relativity: Assignment | Modern Physics PDF Download
Q.1. Two events separated by a (spatial) distance 9 x 109 m, are simultaneous in one inertial frame. Find the time interval between these two events in a frame moving with a constant speed 0.8 c (where the speed of light 3 x 108 m / sec).
Ans.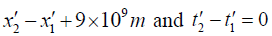
then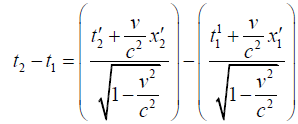

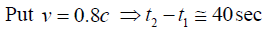
Q.2. Two particles of rest mass m0 approach each other with equal and opposite velocity v in the laboratory frame. What is the total energy of one particle as measured in the rest frame of the other by assuming 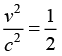
Ans.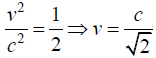
Velocity of one particle with respect to other particle is given by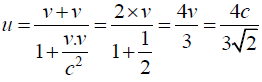
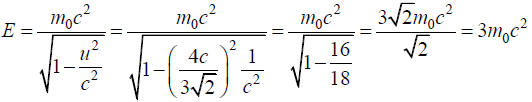
Q.3. In a Lab frame, Particles A and B moves with speed u and v along the Paths Shown in figure. The angle between the trajectories is θ . What is speed of one particle as viewed by the other?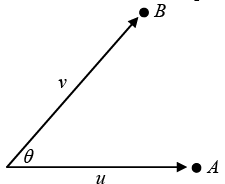
Ans.
Case 1:- speed of B with respect to A choose speed of A along x - axis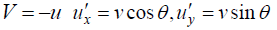
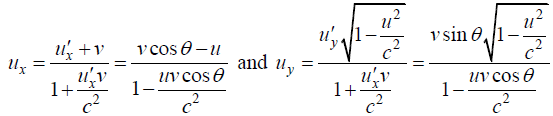
Case 2- speed of A with respect to B choose speed of B along x - axis.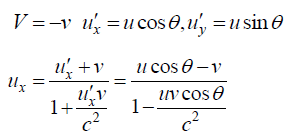
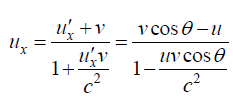
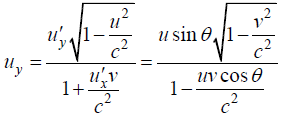
Q.4. The Pions can be produced by bombarding a suitable target in an acceleration with high energy protons, the Pions leaving the target with speed 0.99c. It is found that pions is radioactive elements and its half life is 1.77 x10-8 sec.
(a) find the distance travel by the Pions till its intensity become half of the initial intensity.
(b) with the result find in question a) prove that half life is 1.77 x10-8 sec
Ans.
(a) 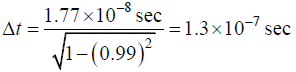
d= 0.99c x Δt = 2.97 x 108 m /sec x 1.3x 10-7 sec = 39m
(b) 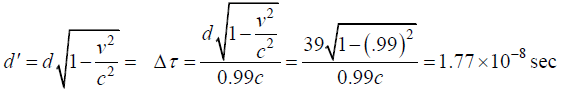
Q.5. Observer 1 sees a particle moving with velocity v on a straight line trajectory inclined at an angle θ to his z axis. Observer 1 is moving with velocity 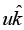 relative to observer 2. derive the formulas for the velocity and direction of motion of particle as by seen observer 2. check that you get the proper result in the limit v→c.
relative to observer 2. derive the formulas for the velocity and direction of motion of particle as by seen observer 2. check that you get the proper result in the limit v→c.
Ans.
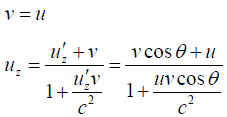
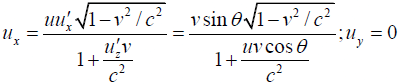
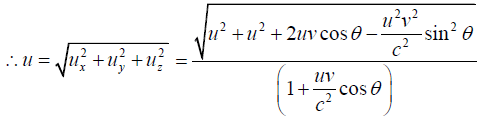
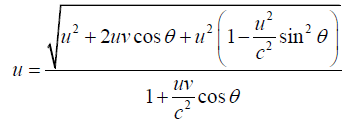
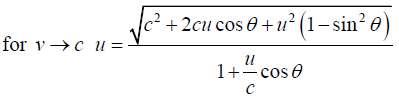
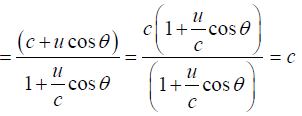
Q.6. A distance galaxy in the constellation hydra is receding from the earth at 6.12 x107 m/sec. by how much is green spectral line of wavelength 500nm emitted by this galaxy shifted the red end of spectrum.
Ans.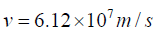
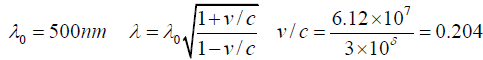
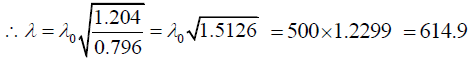
Q.7. A photon of energy E0 bounces off electron initially at rest of rest mass m. Find the energy E of the out going photon ,as function of the scattering angle θ.
Ans.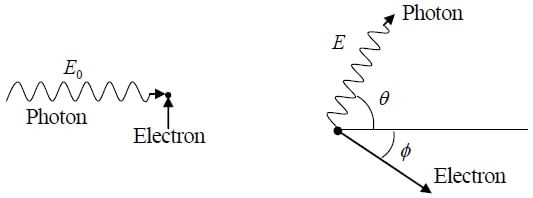
Assume momentum of photon is pp = E/c and momentum of recoil electron is pe. Conservation of momentum in the ‘vertical’’ direction gives pesinϕ = pp sin θ or, since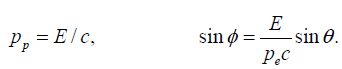
Conservation of momentum in the ‘horizontal’’ direction gives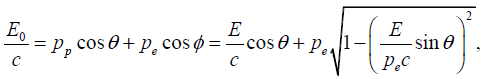
or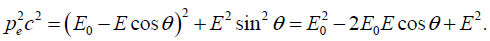
finally, conservation of energy says that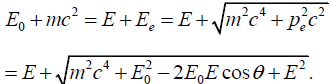
Solving for E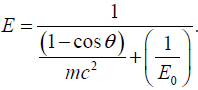
Q.8. Let ( x,t ) and ( x',t') be the coordinate system used by the observers o and o' moves with a velocity v = βc along their Common Positive x axis. If x+ = x+ ct and x- = x- ct are the linear Combinations of the Coordinates.
Write down expression of x'+ as function of f(x+, β) and x'- as function of f(x-,β)
Ans.
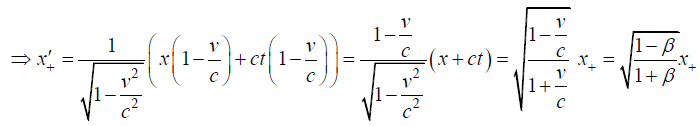
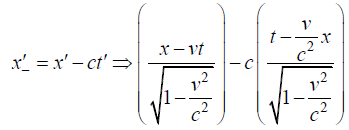
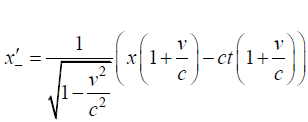
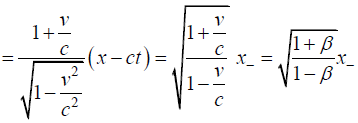
Q.9. A particle of rest mass m is subject to a constant force F .if it is starts from rest at the origin at time t.
(a) prove that velocity 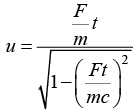
(b) 
(c) plot x(t) V/s t for non relativistic case.
(d) plot x(t) V/s t for relativistic case
Ans.
(a)
But since p = 0 at t = 0 the constant must be zero, and hence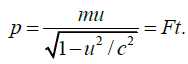
Solving for u, we obtain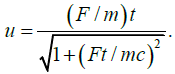
The numerator, of course, is the classical answer –it’s approximately right, if
(F/m)t ≪ c. but the relativistic denominator ensures that u never exceeds c; in fact as t→∞, u→ c to complete the problem we must integrate again:
(b)
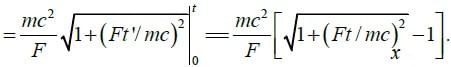
(c) In place of the classical parabola, x(t) = (F/2m)t2,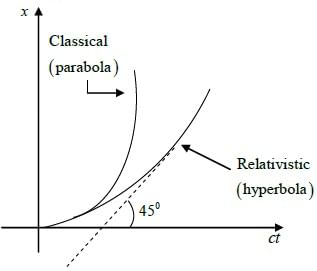
(d) The graph is a hyperbola for this reason, motion under a constant force is often called hyperbolic motion.
Q.10. Consider a radioactive nucleus that is travelling at a speed c/2 with respect to the lab frame. It emits γ-rays of frequency v0 in its rest frame. There is a stationary detector, (which is not on the path of the nucleus) in the lab. If a γ -ray photon is emitted when the nucleus is closest to the detector, then find the frequency observed at the detector.
Ans. Consider a radioactive nucleus that is travelling at a speed c/2 with respect to the lab frame. It emits γ-rays of frequency v0 in its rest frame. There is a stationary detector, (which is not on the path of the nucleus) in the lab. If a γ -ray photon is emitted when the nucleus is closest to the detector, then find the frequency observed at the detector.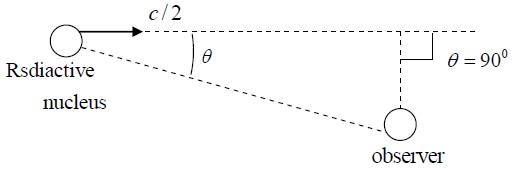


Q.11. A particle with mass m and total energy E0 travels at a constant velocity v which may approach the speed of light. It then collides with a stationary particle with the same mass m, and they are seen to scatter elastically at the relative angle q with equal kinetic energies, then prove that 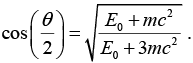
Ans. As the elastically scattered particles have the some mass and the same kinetic
energy, their momenta must make the same angle θ/2 with the incident direction and have
the same magnitude.
Conservation of energy and of momentum give
where E, p are the energy and momentum of each scattered particle Squaring both side
of the energy equation we have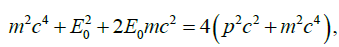
or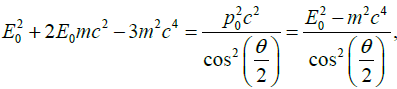
giving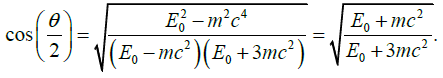
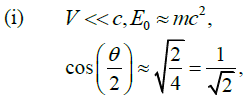
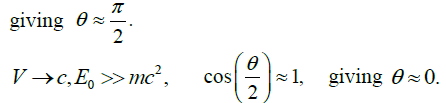
Q.12. In a certain inertial frame, two light pulses are emitted at point 5km apart and separated in time by 5μ sec . An observer moving at a speed v along the line joining these points notes that the pulses are simultaneous. Find the speed of observer.
Ans.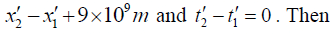
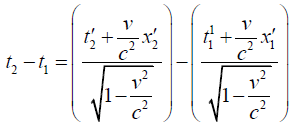
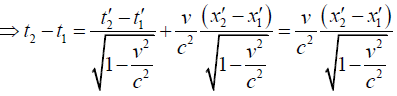
put v = 0.8c ⇒ t2 - t1 ≅ 40 sec
Q.13. Inertial frame B is moving with respect to inertial frame A with speed c/4 in x direction. With respect to frame B , Two particle of rest mass m0 collide with speed c/2 along x axis and stick together after collision.
(a) What will total momentum before collision and after collision measured from frame B
(b) Prove that total momentum before collision and after collision is equal if it is measured from frame A.
Ans. (a) the observer B will see zero momentum before collision
Momentum before collision Pbefore = P - P = 0
Momentum after collision Pafter = 0 so composite mass is assume to be rest with rest mass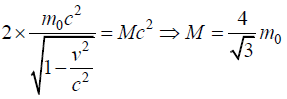
(b) Observer A see the particle before collision
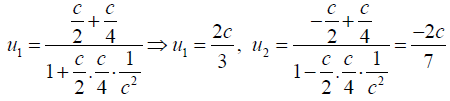
Momentum before collision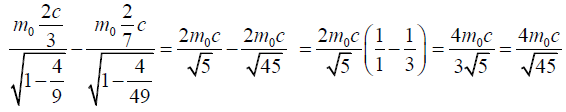
Momentum after collision seen by observer that mass of particle 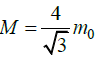 with speed c /4
with speed c /4
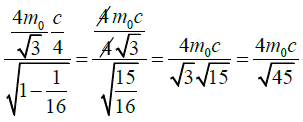
Q.14. A rod of proper length l0 oriented parallel to x axis moves with speed u along the x axis in S frame .if S' frame is moving with speed v along x axis .prove that length measured from S' frame is 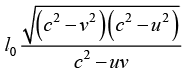
Ans.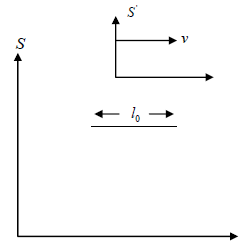
ux = u, V = v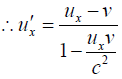
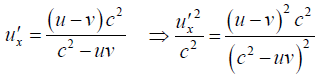
∴ length of rod with respect to S',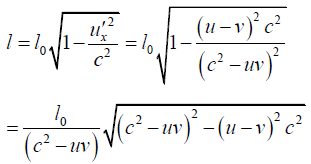

Q.15. Force 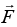 is applied on a particle of relativistic mass m .prove that the acceleration
is applied on a particle of relativistic mass m .prove that the acceleration 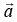 is given by
is given by 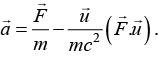
Ans. In general, the force is given by
We Know that m = E/c2 So that 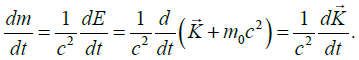
But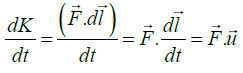
So that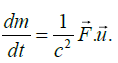
We can now substitute this into Equation and obtain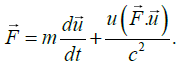
The acceleration a is defined by a = du / dt so that the general expression for acceleration is 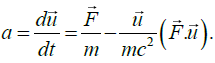
Q.16. Two particles of rest mass m are emitted in the same direction with momenta 5mc and 10mc respectively. As seen the slower one what is the velocity of faster particle?
Ans. In the laboratory frame K0, the slower particle has momentum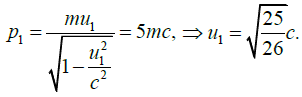
Similarly for the faster particle, 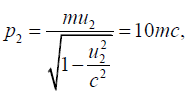 the velocity is
the velocity is
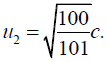
Under usual notation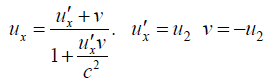
|
37 videos|16 docs|19 tests
|
FAQs on Special Theory of Relativity: Assignment - Modern Physics
| 1. What is the special theory of relativity? |  |
| 2. How does the special theory of relativity explain time dilation? |  |
| 3. Can the special theory of relativity be applied to everyday situations? |  |
| 4. How does the special theory of relativity impact our understanding of the universe? |  |
| 5. Are there any experimental confirmations of the special theory of relativity? |  |

|
Explore Courses for Physics exam
|

|


















